区间DP
区间DP
划分区间,区间长度从1~m。
for(int len=1;len<=m;++len)
for(int i=1;i<=n-len+1;++i)
{
int j=i+len-1;
转移方程
}
石子合并
设有N堆石子排成一排,其编号为1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这N
堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和
,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选
择的顺序不同,合并的总代价也不相同。
例如有4堆石子分别为 1 3 5 2, 我们可以先合并1、2堆,
代价为4,得到4 5 2, 又合并 1,2堆,代价为9,得到9 2
,再合并得到11,总代价为4+9+11=24;
如果第二步是先合并2,3堆,则代价为7,得到4 7,最后一
次合并代价为11,总代价为4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数N表示石子的堆数N。
第二行N个数,表示每堆石子的质量(均不超过1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300
#include<bits/stdc++.h>
using namespace std;
#define maxn 305
int n,a[maxn],f[maxn][maxn];
int main()
{
memset(f,0x3f,sizeof(f));
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),f[i][i]=0,a[i]+=a[i-1];
for(int i=2;i<=n;++i)
for(int l=1;l<=n-i+1;++l)
{
int r=l+i-1;
for(int k=l;k<r;++k)
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]);
f[l][r]+=a[r]-a[l-1];
}
printf("%d",f[1][n]);
}
多边形
“多边形游戏”是一款单人益智游戏。
游戏开始时,给定玩家一个具有N个顶点N条边(编号1-N)的多边形,如图1所示,其中N = 4。
每个顶点上写有一个整数,每个边上标有一个运算符+(加号)或运算符*(乘号)。
第一步,玩家选择一条边,将它删除。
接下来在进行N-1步,在每一步中,玩家选择一条边,把这条边以及该边连接的两个顶点用一个新的顶点代替,新顶点上的整数值等于删去的两个顶点上的数按照删去的边上标有的符号进行计算得到的结果。
下面是用图1给出的四边形进行游戏的全过程。
最终,游戏仅剩一个顶点,顶点上的数值就是玩家的得分,上图玩家得分为0。
请计算对于给定的N边形,玩家最高能获得多少分,以及第一步有哪些策略可以使玩家获得最高得分。
输入格式
输入包含两行,第一行为整数N。
第二行用来描述多边形所有边上的符号以及所有顶点上的整数,从编号为1的边开始,边、点、边…按顺序描述。
其中描述顶点即为输入顶点上的整数,描述边即为输入边上的符号,其中加号用“t”表示,乘号用“x”表示。
输出格式
输出包含两行,第一行输出最高分数。
在第二行,将满足得到最高分数的情况下,所有的可以在第一步删除的边的编号从小到大输出,数据之间用空格隔开。
数据范围
3≤N≤503≤N≤50,
数据保证无论玩家如何操作,顶点上的数值均在[-32768,32767]之内。
输入样例:
4
t -7 t 4 x 2 x 5
输出样例:
33
1 2
#include<bits/stdc++.h>
using namespace std;
#define maxn 105
int n,ans,head,q[maxn],a[maxn],f[2][maxn][maxn];
//0:max 1:min
bool b[maxn];
//0:* 1:+
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
char op[2];
scanf("%s %d",&op,&a[i]);
if(op[0]=='t') b[i-1]=1;
}
for(int i=n+1;i<=n*2;++i)
b[i-1]=b[i-1-n];
memset(f[0],0x80,sizeof(f[0]));
memset(f[1],0x3f,sizeof(f[1]));
for(int i=1;i<=n*2;++i)
for(int u=0;u<=1;++u)
f[u][i][i]=i-n>0?a[i-n]:a[i];
for(int i=2;i<=n;++i)
for(int l=1;l<=n*2-i+1;++l)
{
int r=l+i-1;
for(int k=l;k<r;++k)
{
if(b[k])
{
f[0][l][r]=max(f[0][l][r],f[0][l][k]+f[0][k+1][r]);
f[1][l][r]=min(f[1][l][r],f[1][l][k]+f[1][k+1][r]);
}
else
{
for(int x=0;x<=1;++x)
for(int y=0;y<=1;++y)
{
int val=f[x][l][k]*f[y][k+1][r];
f[0][l][r]=max(f[0][l][r],val);
f[1][l][r]=min(f[1][l][r],val);
}
}
}
}
for(int l=1;l<=n;++l)
{
int val=f[0][l][l+n-1];
if(val<ans) continue;
if(val>ans) ans=val,head=0;
q[++head]=l;
}
printf("%d\n",ans);
for(int i=1;i<=head;++i) printf("%d ",q[i]);
}
金字塔
虽然探索金字塔是极其老套的剧情,但是有一队探险家还是到了某金字塔脚下。
经过多年的研究,科学家对这座金字塔的内部结构已经有所了解。
首先,金字塔由若干房间组成,房间之间连有通道。
如果把房间看作节点,通道看作边的话,整个金字塔呈现一个有根树结构,
节点的子树之间有序,金字塔有唯一的一个入口通向树根。
并且,每个房间的墙壁都涂有若干种颜色的一种。
探险队员打算进一步了解金字塔的结构,为此,他们使用了一种特殊设计的
机器人。
这种机器人会从入口进入金字塔,之后对金字塔进行深度优先遍历。
机器人每进入一个房间(无论是第一次进入还是返回),都会记录这个房间
的颜色。
最后,机器人会从入口退出金字塔。
显然,机器人会访问每个房间至少一次,并且穿越每条通道恰好两次(两个
方向各一次), 然后,机器人会得到一个颜色序列。
但是,探险队员发现这个颜色序列并不能唯一确定金字塔的结构。
现在他们想请你帮助他们计算,对于一个给定的颜色序列,有多少种可能的
结构会得到这个序列。
因为结果可能会非常大,你只需要输出答案对109 取模之后的值。
输入格式
输入仅一行,包含一个字符串S,长度不超过300,表示机器人得到的颜色序列。
输出格式
输出一个整数表示答案。
输入样例:
ABABABA
输出样例:
5
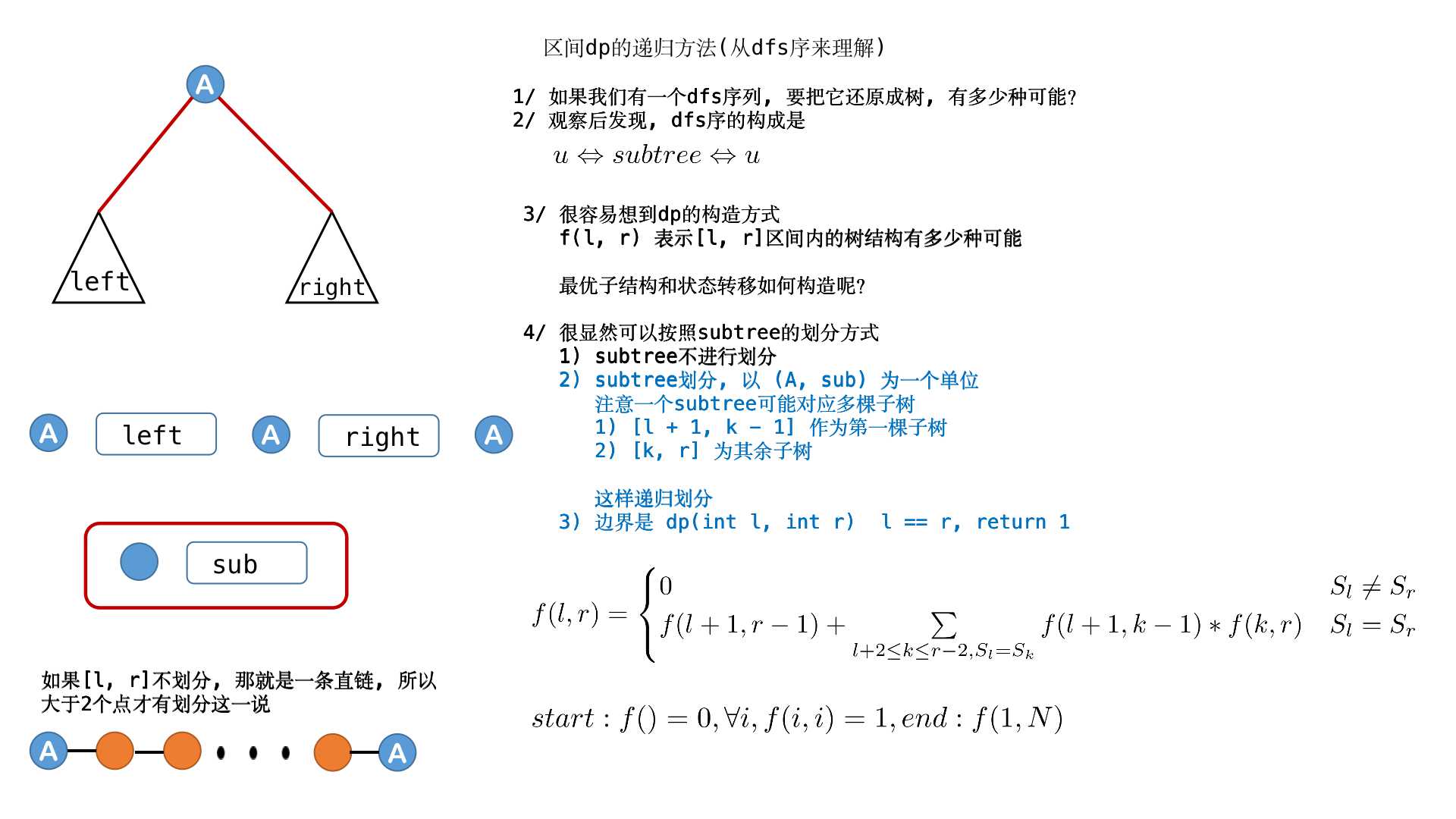
#include<bits/stdc++.h>
using namespace std;
string s;
long long f[305][305],p=1e9;
long long dfs(int l,int r)
{
if(f[l][r]==-1)
{
if(l==r) f[l][r]=1;
else
{
f[l][r]=0;
for(int k=l+2;k<=r;++k)
if(s[l]==s[k]) f[l][r]=(f[l][r]+dfs(l+1,k-1)*dfs(k,r))%p;
}
}
return f[l][r];
}
int main()
{
cin>>s;
memset(f,-1,sizeof(f));
dfs(0,s.length()-1);
printf("%lld",f[0][s.length()-1]);
}
折叠序列
比尔正在试图用折叠重复子序列的方式紧凑的表示由大写字母
’A’到’Z’组成的字符序列。
例如,表示序列AAAAAAAAAABABABCCD的一种方式是10(A)2(BA)B2(C)D。
他通过以下方式定义了折叠的字符序列以及它们的展开变换:
1、包含带个字符的序列被认为是折叠序列,展开它得到的序列
为它本身。
2、如果S和Q是两个折叠序列,并且S可以展开得到S’,Q可以展
开得到Q’,则认为SQ也是一个折叠序列,并且SQ展开得到S’Q’。
3、如果S是折叠序列,则X(S)也是折叠序列,其中X为大于1的整数。
如果S展开得到S’,则X(S)展开得到X个S’。
根据定义可以展开任意给出的折叠序列,现在给出原序列,请你将
它折叠,并使得折叠序列包含尽可能少的字符数。
输入格式
输入包含一行由大写字母构成的字符序列,序列长度在1到100之间。
输出格式
输出包含字符数最少的折叠序列,如果答案不唯一则任意输出一个即可。
输入样例:
输出样例:
AAAAAAAAAABABABCCD
输出样例:
9(A)3(AB)CCD

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3fffffff
char a[105],s[105][105][105];
int n,f[105][105];
int main()
{
cin>>a+1;
n=strlen(a+1);
for(int i=1;i<=n;++i) f[i][i]=1,s[i][i][0]=a[i];
// cout<<n<<endl;
for(int len=2;len<=n;++len)
for(int i=1;i<=n-len+1;++i)
{
int j=i+len-1;
f[i][j]=INF;
//folding_begin
// cout<<i<<" "<<j;
for(int k=1;k<=len/2;++k)
{
if(len%k) continue;
int xx=i,yy=i+k;
while(a[xx]==a[yy]&&yy<=j) ++xx,++yy;
if(yy>j)
{
int cnt=len/k;
sprintf(s[i][j],"%d", cnt);
strcat(s[i][j],"(");
strcat(s[i][j],s[i][i+k-1]);
strcat(s[i][j],")");
f[i][j]=strlen(s[i][j]);
break;
}
}
//folding_end
for(int k=i;k<j;++k)
if(f[i][j]>f[i][k]+f[k+1][j])
{
f[i][j]=f[i][k]+f[k+1][j];
strcpy(s[i][j],s[i][k]);
strcat(s[i][j],s[k+1][j]);
}
// printf("%d %d==%s\n",i,j,s[i][j]);
}
printf("%s\n",s[1][n]);
}
消木块
你们中的一些人可能玩过一个叫做消木块的游戏。
n个木块排成一列,每个木块都有一个颜色。
例如下图中木块的颜色分别为:金,银,银,银,银,铜,铜,铜,金。
每次,你都可以点击一个木块,这样被点击的木块
以及和它相邻并且同色的木块就会消除。
如果一次性消除了k个木块,那么就会得到k*k分。
例如下图所示,点击银色木块,四个木块被消去,
得到16分。
给定你一个游戏初始状态,请你求出最高得分是多少。
输入格式
第一行包含整数t,表示共有t组测试数据。
每组数据第一行包含整数n,表示共有n个木块。
第二行包含n个整数,表示n个木块的颜色。
代表木块颜色的整数范围是1~n。
输出格式
每组数据输出一个结果,每个结果占一行。
输出格式为“Case x: y”,其中x为数据组别编号,
从1开始,y为结果。
数据范围
1≤n≤200
输入样例:
2
9
1 2 2 2 2 3 3 3 1
1
1
输出样例:
输出样例:
Case 1: 29
Case 2: 1
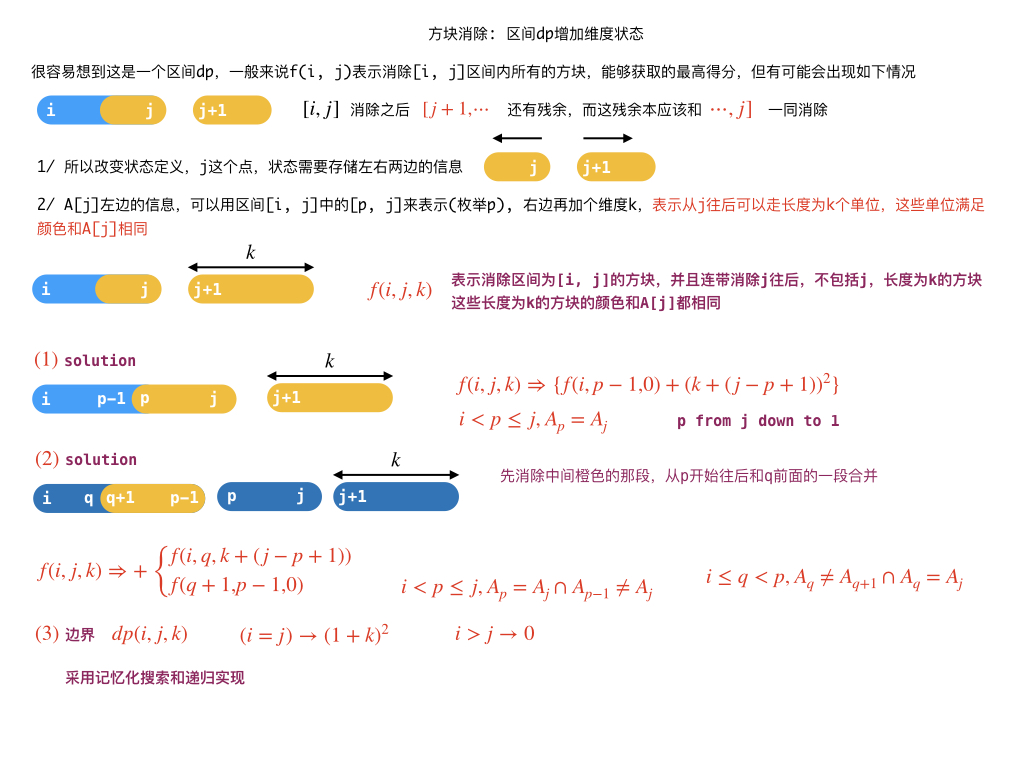
#include<bits/stdc++.h>
using namespace std;
int n,t,a[205],f[205][205][205];
int dp(int i,int j,int k)
{
if(i>j) return 0;
int &ans=f[i][j][k];
if(i==j) return ans=(k+1)*(k+1);
if(ans>=0) return ans;
int p=j;
while(a[p]==a[j]&&p>=i) p--;
p++;
ans=dp(i,p-1,0)+(k+j-p+1)*(k+j-p+1);
for(int q=i;q<p;++q)
if(a[q]==a[j]&&a[q+1]!=a[q])
ans=max(ans,dp(i,q,k+j-p+1)+dp(q+1,p-1,0));
//消除q~p,进行合并。
return ans;
}
int main()
{
scanf("%d",&t);
for(int yuo=1;yuo<=t;++yuo)
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
memset(f,-1,sizeof(f));
printf("Case %d: %d\n",yuo,dp(1,n,0));
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号