背包问题
背包问题
0/1背包
给定n个物品,其中第i个物品体积为vi,价值为wi。有一容积为w的背包,放一些物品入背包,使物品的总体积不超过w,且价值最大
\(f[i][j]=max(f[i-1][j],f[i-1,j-vi]+wi【if(j>=vi)】)\)
数字组合
给定N个正整数A1,A2,…,AN,从中选出若干个数,使它们的和为M,求有多少种选择方案。
输入格式
第一行包含两个整数N和M。
第二行包含N个整数,表示A1,A2,…,AN。
输出格式
包含一个整数,表示可选方案数。
数据范围
1≤N≤100,
1≤M≤10000,
1≤Ai≤1000
输入样例:
4 4
1 1 2 2
输出样例:
3
#include<bits/stdc++.h>
using namespace std;
#define maxn 105
#define maxm 10005
int n,m,f[maxm],a[maxn];
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+n+1);
f[0]=1;
for(int i=1;i<=n;++i)
{
for(int j=m;j;--j)
{
if(j-a[i]<0) break;
f[j]+=f[j-a[i]];
}
}
printf("%d",f[m]);
}
完全背包
给定n个物品,其中第i个物品体积为vi,价值为wi,并且有无数个。有一容积为w的背包,放一些物品入背包,使物品的总体积不超过w,且价值最大。
\(f[i][j]=max(f[i-1][j],f[i,j-vi]+wi【if(j>=vi)】)\)
\(f[j]\)正序循环表示使用无数次
自然数拆分
给定一个自然数N,要求把N拆分成若干
个正整数相加的形式,参与加法运算的
数可以重复。
注意:
拆分方案不考虑顺序;
至少拆分成2个数的和。
求拆分的方案数 mod 2147483648的结果。
输入格式
一个自然数N。
输出格式
输入一个整数,表示结果。
数据范围
1≤N≤4000
输入样例:
7
输出样例:
输出样例:
14
#include<bits/stdc++.h>
using namespace std;
#define p 2147483648
int n,f[4005];
int main()
{
scanf("%d",&n);
f[0]=1;
for(int i=1;i<n;++i)
for(int j=i;j<=n;++j)
f[j]=(f[j]+f[j-i])%p;
printf("%d",f[n]);
}
陪审团
在一个遥远的国家,一名嫌疑犯是否有罪需要由陪审团来决定。
陪审团是由法官从公民中挑选的。
法官先随机挑选N个人(编号1,2…,N)作为陪审团的候选人,然后再从这N个人中按照下列方法选出M人组成陪审团。
首先,参与诉讼的控方和辩方会给所有候选人打分,分值在0到20之间。
第 i 个人的得分分别记为p[i]和d[i]。
为了公平起见,法官选出的M个人必须满足:辩方总分D和控方总分P的差的绝对值|D-P|最小。
如果选择方法不唯一,那么再从中选择辨控双方总分之和D+P最大的方案。
求最终的陪审团获得的辩方总分D、控方总分P,以及陪审团人选的编号。
注意:若陪审团的人选方案不唯一,则任意输出一组合法方案即可。
输入格式
输入包含多组测试数据。
每组测试数据第一行包含两个整数N和M。
接下来N行,每行包含两个整数p[i]和d[i]。
每组测试数据之间隔一个空行。
当输入数据N=0,M=0时,表示结束输入,该数据无需处理。
输出格式
对于每组数据,第一行输出’Jury #C’,C为数据编号,
从1开始。
第二行输出“Best jury has value P for prosecution
and value D for defence:”,P为控方总分,D为辩方总分。
第三行输出按升序排列的陪审人选编号,每个编号前输出一
个空格。
每组数据输出完后,输出一个空行。
数据范围
1≤N≤200,
1≤M≤20
0≤p[i],d[i]≤20
输入样例:
4 2
1 2
2 3
4 1
6 2
0 0
输出样例:
输出样例:
Jury #1
Best jury has value 6 for prosecution
and value 4 for defence:
2 3
用f[i][j][k]表示从前i个人中选j个人且总差为k的所有方案中的总分最大的方案的总分。
我们维护这个数组,再找出最小的差值v,那么最大分数的方案即为f[n][m][v]所对应的方案。
由于分数0——20,那么一个人的差值(p-d)范围在-20——20,20个人总差值就为-400——400。
定一个偏移量base=400,全部加上base即可使总差值变为0——800。
#include<bits/stdc++.h>
using namespace std;
int n,m,tot,D,P,a[205],b[205],sub[205],add[205],f[25][805];
vector<int>pt[25][805];
int main()
{
while(~scanf("%d %d",&n,&m))
{
if(m==0||n==0) return 0;
memset(f,-1,sizeof(f));
int fix=m*20;
f[0][fix]=0;
for(int i=1;i<=n;i++)
{
scanf("%d %d",&a[i],&b[i]);
sub[i]=a[i]-b[i];
add[i]=a[i]+b[i];
}
for(int i=1;i<=n;++i)
for(int j=m-1;j>=0;--j)
for(int k=0;k<2*fix;++k)
{
if(f[j][k]>=0&&f[j+1][k+sub[i]]<=f[j][k]+add[i])
{
f[j+1][k+sub[i]]=f[j][k]+add[i];
pt[j+1][k+sub[i]]=pt[j][k];
pt[j+1][k+sub[i]].push_back(i);
}
}
int k;
for(k=0;k<=fix;++k)
if(f[m][fix-k]>=0||f[m][fix+k]>=0) break;
int div;
if(f[m][fix-k]>f[m][fix+k]) div=fix-k;
else div=fix+k;
printf("Jury #%d\nBest jury has value %d for prosecution and value %d for defence:\n",++tot,(f[m][div]+div-fix)/2,(f[m][div]-div+fix)/2);
for(int i=0;i<m;i++)
printf(" %d",pt[m][div][i]);
printf("\n\n");
}
多重背包
给定n个物品,其中第i个物品体积为vi,价值为wi,并且有ci个。有一容积为w的背包,放一些物品入背包,使物品的总体积不超过w,且价值最大。
直接拆分
for(int i=1;i<=n;++i)
for(int j=1;j<=c[i];++j)
for(int k=m;k>=v[i];--k)
f[k]=max(f[k],f[k-v[i]]+w[i]);
二进制拆分
for(int i=1;i<=n;++i)
{
for(int j=1;j<=c[i];c[i]-=j,j<<=1)
for(int k=m;k>=v[i]*j;--k)
f[k]=max(f[k],f[k-v[i]*j]+w[i]*j);
if(c[i])
for(int k=m;k>=v[i]*m;--k)
f[k]=max(f[k],f[k-v[i]*c[i]]+w[i]*c[i]);
}
多重背包问题 II
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包
容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数
和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,
分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000
提示:
本题考查多重背包的二进制优化方法。
输入样例:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
#include<bits/stdc++.h>
using namespace std;
#define maxn 2005
int n,m,v,w,s;
int f[maxn];
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
{
scanf("%d %d %d",&v,&w,&s);
for(int j=1;s>j;s-=j,j<<=1)
for(int k=m;k>=j*v;--k)
f[k]=max(f[k],f[k-j*v]+j*w);
for(int k=m;k>=s*v;--k)
f[k]=max(f[k],f[k-s*v]+s*w);
}
printf("%d",f[m]);
}
划分大理石
有价值分别为 1..6 的大理石各 a[1..6]块,现要将它们分成两部分,使得两部分价
值之和相等,问是否可以实现。
其中大理石的总数不超过 20000。
输入格式
输入包含多组数据!
每组数据占一行,包含 6 个整数,表示 a[1]~a[6]。
当输入为 0 0 0 0 0 0 时表示输入结束,且该行无需考虑。
输出格式
每组数据输出一个结果,每个结果占一行。
如果可以实现则输出“Can”,否则输出“Can’t”
输入样例:
4 7 4 5 9 1
9 8 1 7 2 4
6 6 8 5 9 2
1 6 6 1 0 7
5 9 3 8 8 4
0 0 0 0 0 0
输出样例:
Can't
Can
Can't
Can't
Can
#include<bits/stdc++.h>
using namespace std;
#define N 20000*6+5
int a[10],q[N];
bool f[N];
int main()
{
// freopen("divide.in","r",stdin);
// freopen("divide.out","w",stdout);
while(~scanf("%d %d %d %d %d %d",&a[1],&a[2],&a[3],&a[4],&a[5],&a[6]))
{
bool bz=1;
for(int i=1;i<=6;i++)
if(a[i]){bz=0;break;}
if(bz) return 0;
int val=0;
for(int i=1;i<=6;++i) val+=a[i]*i;
if(val&1) {printf("Can't\n");continue;}
val/=2;
memset(f,0,sizeof(f));f[0]=1;
q[0]=0;
q[++q[0]]=0;
for(int i=1;i<=6;++i)
{
for(int j=0;j<=val;++j)
{
if(f[j]>=0) f[j]=a[i];
else if(j>=i&&f[j-i]>=0) f[j]=f[j-i]-1;
else f[j]=-1;
}
if(f[val]!=-1) break;
}
if(f[val]!=-1) printf("Can\n");
else printf("Can't\n");
}
}
P6418 ZABAVA
题目描述
一座新的公寓开放了,这座公寓有 mm 栋楼。
现在会有 nn 个学生,每一天都会进来一个人。
一栋楼进来一个人后,会进行一场派对,派对会有与当前人数相等的吵闹指数。
但是,现在可以进行 kk 次操作,每一次操作可以将一栋楼里的全部学生踢出这座新公寓。
请注意,学生先进楼,然后才能进行操作。
现在求出最小吵闹指数的相加之和。
你不必使用完全部的操作。
输入格式
第一行为三个整数 n,m,kn,m,k。
接下来 nn 行,一行一个整数 pp,第 ii 行表示在第 ii 天,第 ii 个同学搬进了第 pp 栋楼。
输出格式
仅一行,表示最小吵闹指数的相加之和。
输入输出样例
输入 #1复制
5 1 2
1
1
1
1
1
输出 #1复制
7
输入 #2复制
11 2 3
1
2
1
2
1
2
1
2
1
2
1
输出 #2复制
18
说明/提示
样例说明
样例输入输出 1 说明
可以在第一天和第三天清空第一栋楼,这样每一天的吵闹指数为 1,1,2,1,2,如果不清空每一天的吵闹指数为 1,2,3,4,5。
样例输入输出 2 说明
在第四天和第八天清空第一栋楼,在第六天清空第二栋楼,这样每一天的吵闹指数为 1,1,2,2,1,3,2,1,1,2,2。
数据范围及限制
- 对于 4040 分的数据,保证 m=1m=1。
- 对于 6060 分的数据,保证 n\le 10^3n≤103。
- 对于 8080 分的数据,保证 n\le 5\times 10^4n≤5×104。
- 对于 100%100% 的数据,保证 1\le n\le 10^61≤n≤106,1\le m\le 1001≤m≤100,1\le k\le 5001≤k≤500,1\le p\le m1≤p≤m。
题意:给出m(不一定等于题中输入的m)个长度不等的序列,将每个序列拆分成k段,\(sum(k)+m<=K\),每一段的值为(设\(len\)为段的长度)\(len*(len+1)/2\),使所有值的和最小。
\(DP[i][j]:\)前\(i\)个序列一共拆分成了\(k+i\)个的值。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=105,K=505;
int n,m,k,ans,cnt[N],dp[K],sum[K];
//dp[i][j]=min__(dp[i-1][j-k]+js(a[i],k))
int calc(int x,int y)
{
if(y>x) return dp[k+1];
int t=x/y;
return t*(t+1)/2*y+(t+1)*(x%y);
}
signed main()
{
scanf("%lld %lld %lld",&n,&m,&k);
for(int i=1,x;i<=n;++i) scanf("%lld",&x),cnt[x]++;
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=m;++i)
{
if(cnt[i]==0) continue;
for(int j=0;j<=k;++j) sum[j]=calc(cnt[i],j+1);
for(int j=k;j>=0;--j)
{
dp[j]+=sum[0];
for(int s=1;s<=j;++s)
dp[j]=min(dp[j],dp[j-s]+sum[s]);
}
}
ans=dp[k+1];
for(int i=0;i<=k;++i) ans=min(ans,dp[i]);
printf("%lld",ans);
}
单调队列
for(int i=1;i<=n;++i)
{
memcpy(f[0],f[1],sizeof(f[1]));
scanf("%d %d %d",&v,&w,&c);
for(int j=0;j<v;++j)
{
int head=1,tail=0;
for(int k=j;k<=m;k+=v)
{
f[1][k]=f[0][k];
if(head<=tail&&q[head]+c*v<k) head++;
if(head<=tail) f[1][k]=max(f[0][k],f[0][q[head]]+(k-q[head])/v*w);
while(head<=tail&f[0][q[tail]]-(q[tail]-j)/v*w<f[0][k]-(k-j)/v*w) tail--;
q[++tail]=k;
}
}
}
单调队列模板
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,
且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V (0<N≤1000, 0<V≤20000),用空格隔开,
分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,
分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V≤20000
0<vi,wi,si≤20000
提示
本题考查多重背包的单调队列优化方法。
输入样例:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
#include<bits/stdc++.h>
using namespace std;
int n,m,c,v,w,head,tail;
int f[2][20005],q[20005];
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
{
memcpy(f[0],f[1],sizeof(f[1]));
scanf("%d %d %d",&v,&w,&c);
for(int j=0;j<v;++j)
{
int head=1,tail=0;
for(int k=j;k<=m;k+=v)
{
f[1][k]=f[0][k];
if(head<=tail&&q[head]+c*v<k) head++;
if(head<=tail) f[1][k]=max(f[0][k],f[0][q[head]]+(k-q[head])/v*w);
while(head<=tail&f[0][q[tail]]-(q[tail]-j)/v*w<f[0][k]-(k-j)/v*w) tail--;
q[++tail]=k;
}
}
}
printf("%d",f[1][m]);
}
贪心
一般只关注状态不关注值
硬币
给定N种硬币,其中第 i 种硬币的面值为AiAi,共有CiCi个。
从中选出若干个硬币,把面值相加,若结果为S,则称“面值S能被拼成”。
求1~M之间能被拼成的面值有多少个。
输入格式
输入包含多组测试用例。
每组测试用例第一行包含两个整数N和M。
第二行包含2N个整数,分别表示A1,A2,…,ANA1,A2,…,AN和C1,C2,…,CNC1,C2,…,CN。
当输入用例N=0,M=0时,表示输入终止,且该用例无需处理。
输出格式
每组用例输出一个结果,每个结果占一行。
数据范围
1≤N≤100
1≤M≤105
1≤Ai≤105
1≤Ci≤1000
输入用例:
3 10
1 2 4 2 1 1
2 5
1 4 2 1
0 0
输出用例:
8
4
f[j]表示在i阶段中能否拼出面值为j的情况;
由于本题仅关注“可行性”(面值是否能拼成)而非“最优性”所以根据动态规划的过程我们可以发现,若前i种硬币能拼成面值j,那么只有两种可能的情况
1
前i-1种硬币就能拼成面值j,即在第i阶段开始前,f[j]已经成为true。
2
使用了第i种硬币,即在第i阶段的递推过程中,发现f[j-a[i]]为true,从而使用一个i硬币,使f[j]变为true。
于是可以考虑一种贪心策略:设used[j]表示在第i阶段下将f[j]变为true至少需要使用多少枚第i种硬币。
为了满足我们的贪心策略,我们应该尽量多的使用第1种情况,也就是说在f[j-a[i]]为true时,若f[j]已经为true,就不进行DP转移,并令used[j]=0(我们并没有使用第i种硬币)仅当f[j-a[i]]为true而f[j]为false且已经使用的i硬币used[j-a[i]]<c[i]时,我们使用一个i硬币使f[j]变为true,\(used[j]=used[j-a[i]]+1\);
#include<bits/stdc++.h>
using namespace std;
int n,m,a[101],c[101],used[100005];
bool f[100005];
int main()
{
f[0]=1;
while(~scanf("%d %d",&n,&m))
{
if(!m||!n) return 0;
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&c[i]);
for(int i=1;i<=m;++i) f[i]=0;
for(int i=1;i<=n;++i)
{
if(a[i]>m) continue;
for(int j=1;j<=m;j++) used[j]=0;
for(int j=a[i];j<=m;j++)
if(!f[j]&&f[j-a[i]]&&used[j-a[i]]<c[i])
{
f[j]=1;
used[j]=used[j-a[i]]+1;
}
}
int ans=0;
for(int i=1;i<=m;++i) if(f[i]) ans++;
printf("%d\n",ans);
}
}
划分大理石
有价值分别为 1..6 的大理石各 a[1..6]块,现要将它们分成两部分,使得两部分价
值之和相等,问是否可以实现。
其中大理石的总数不超过 20000。
输入格式
输入包含多组数据!
每组数据占一行,包含 6 个整数,表示 a[1]~a[6]。
当输入为 0 0 0 0 0 0 时表示输入结束,且该行无需考虑。
输出格式
每组数据输出一个结果,每个结果占一行。
如果可以实现则输出“Can”,否则输出“Can’t”
输入样例:
4 7 4 5 9 1
9 8 1 7 2 4
6 6 8 5 9 2
1 6 6 1 0 7
5 9 3 8 8 4
0 0 0 0 0 0
输出样例:
Can't
Can
Can't
Can't
Can
#include<bits/stdc++.h>
using namespace std;
#define N 20000*6+5
int a[10],q[N];
bool f[N];
int main()
{
// freopen("divide.in","r",stdin);
// freopen("divide.out","w",stdout);
while(~scanf("%d %d %d %d %d %d",&a[1],&a[2],&a[3],&a[4],&a[5],&a[6]))
{
bool bz=1;
for(int i=1;i<=6;i++)
if(a[i]){bz=0;break;}
if(bz) return 0;
int val=0;
for(int i=1;i<=6;++i) val+=a[i]*i;
if(val&1) {printf("Can't\n");continue;}
val/=2;
memset(f,0,sizeof(f));f[0]=1;
q[0]=0;
q[++q[0]]=0;
for(int i=1;i<=6;++i)
{
for(int j=0;j<=val;++j)
{
if(f[j]>=0) f[j]=a[i];
else if(j>=i&&f[j-i]>=0) f[j]=f[j-i]-1;
else f[j]=-1;
}
if(f[val]!=-1) break;
}
if(f[val]!=-1) printf("Can\n");
else printf("Can't\n");
}
}
树状背包
有 N 个物品和一个容量是 VV的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
则枚举分给每个子树k空间时得到的最大值
void dfs(int x)
{
for(int i=v[x];i<=m;++i) f[x][i]=w[x];
for(int i=0;i<q[x].size();++i)
{
dfs(q[x][i]);
for(int j=m;j>=v[x];--j)
for(int k=0;k<=j-v[x];++k)
f[x][j]=max(f[x][j],f[x][j-k]+f[q[x][i]][k]);
}
}
树状背包模板
有 N 个物品和一个容量是 VV的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
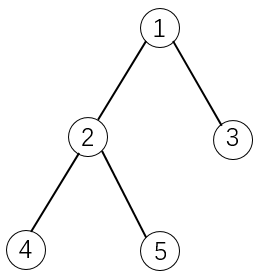
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 ii,体积是 vivi,价值是 wiwi,依赖的父节点编号是 pipi。物品的下标范围是 1…N1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,VN,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 NN 行数据,每行数据表示一个物品。
第 ii 行有三个整数 vi,wi,pivi,wi,pi,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1pi=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
数据范围
1≤N,V≤1001≤N,V≤100
1≤vi,wi≤1001≤vi,wi≤100
父节点编号范围:
- 内部结点:1≤pi≤N1≤pi≤N;
- 根节点 pi=−1pi=−1;
输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例:
11
计算每个子树,分给每个子树k空间时的最大值
#include<bits/stdc++.h>
using namespace std;
int n,m,root,head,tail,v[105],w[105],f[105][105];
deque<int>q[105];
void dfs(int x)
{
for(int i=v[x];i<=m;++i) f[x][i]=w[x];
for(int i=0;i<q[x].size();++i)
{
dfs(q[x][i]);
for(int j=m;j>=v[x];--j)
for(int k=0;k<=j-v[x];++k)
f[x][j]=max(f[x][j],f[x][j-k]+f[q[x][i]][k]);
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,x;i<=n;i++)
{
scanf("%d %d %d",&v[i],&w[i],&x);
if(x==-1) root=i;
else q[x].push_back(i);
}
dfs(root);
printf("%d",f[root][m]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号