主席树
主席树
1.普通主席树
静态区间查询第k大的数。
对于一个长度为n数组,数值离散化之后范围为1~\(s[0]\),则开n棵范围s[0]棵线段树,每次查询l,r区间时,取出树r和树l-1进行计算,树r-树l-1得到的就是树l-r的值。
但由于每个点开一个线段树内存消耗很大,同时易知每棵树和前一棵树相比,只有一条链上的值发生了变化,其他部分和前一刻树可以重叠。故可以把线段树记为以下形式:
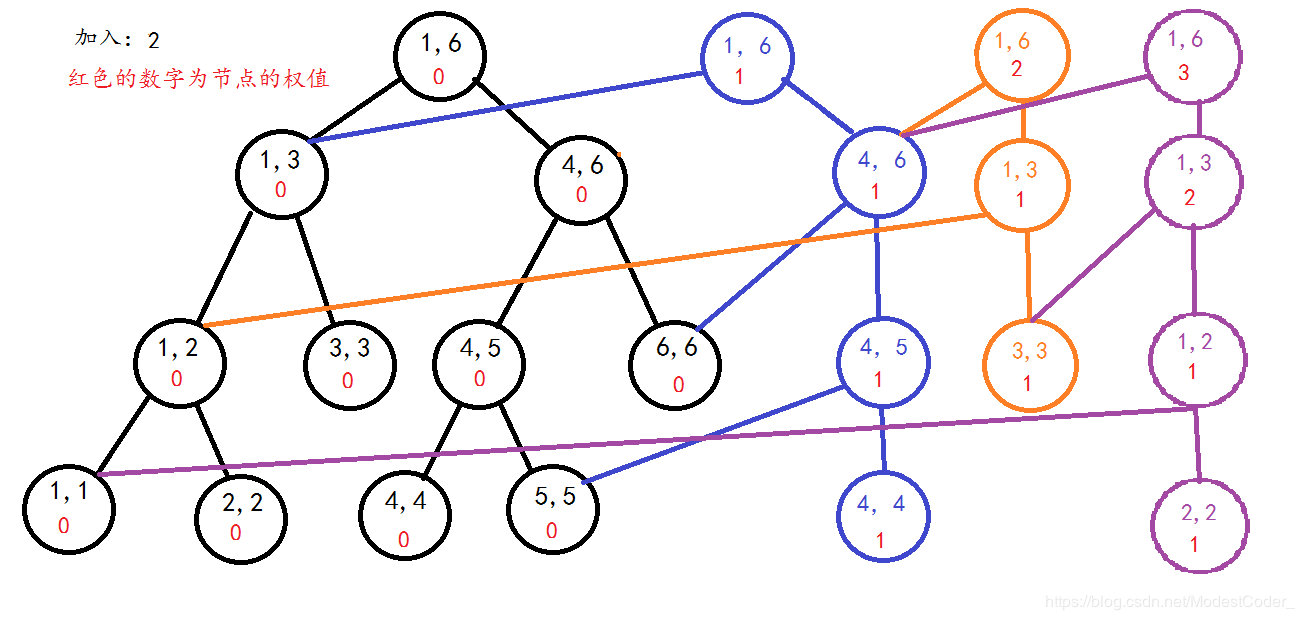
、
模板题:P3834
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,tt,a[N],s[N],root[N],cur[N<<2];
struct t_
{
int ls,rs,val;
}t[N<<5];
void build(int l,int r,int x,int &p,int cp)
{
if(p) return;
p=++tt;
if(l==r)
{
if(l==x) t[p].val=t[cur[cp]].val+1;
cur[cp]=p;
return;
}
int m=(l+r)/2;
if(x<=m) t[p].rs=t[cur[cp]].rs;
else t[p].ls=t[cur[cp]].ls;
build(l,m,x,t[p].ls,cp*2);
build(m+1,r,x,t[p].rs,cp*2|1);
t[p].val=t[t[p].ls].val+t[t[p].rs].val;
cur[cp]=p;
}
void dfs(int x,int l,int r)
{
if(l==r) return;
int m=(l+r)/2;
dfs(t[x].ls,l,m);
dfs(t[x].rs,m+1,r);
}
int query(int l,int r,int k,int p1,int p2)
{
if(l==r) return l;
int m=(l+r)/2,val=t[t[p2].ls].val-t[t[p1].ls].val;
return k<=val?query(l,m,k,t[p1].ls,t[p2].ls):query(m+1,r,k-val,t[p1].rs,t[p2].rs);
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),s[i]=a[i];
sort(s+1,s+n+1);
s[0]=unique(s+1,s+n+1)-s-1;
for(int i=1;i<=n;++i) a[i]=lower_bound(s+1,s+s[0]+1,a[i])-s;
for(int i=1;i<=n;++i) build(1,s[0],a[i],root[i],1);
for(int i=1,l,r,k;i<=m;++i)
{
scanf("%d %d %d",&l,&r,&k);
printf("%d\n",s[query(1,s[0],k,root[l-1],root[r])]);
}
}
P4137 Rmq Problem / mex
查询一段区间内最小的没有出现过的自然数。
可以知道这个答案要么是0,要么是\(a[i]+1\),所以把这两种数字都加入离散化的列表。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=4e5+5;
int n,m,a[N],root[N],s[M];
int tt,lc[M<<5],rc[M<<5],val[M<<5];
void build(int l,int r,int &p)
{
p=++tt;
if(l==r) return;
int mid=(l+r)>>1;
build(l,mid,lc[p]);
build(mid+1,r,rc[p]);
}
void insert(int l,int r,int x,int d,int &p1,int p2)
{
p1=++tt;
if(l==r){val[p1]=d;return;}
int mid=(l+r)>>1;
if(x<=mid) insert(l,mid,x,d,lc[p1],lc[p2]),rc[p1]=rc[p2];
else insert(mid+1,r,x,d,rc[p1],rc[p2]),lc[p1]=lc[p2];
val[p1]=min(val[lc[p1]],val[rc[p1]]);
}
int ask(int l,int r,int x,int p)
{
if(l==r) return s[l];
int mid=(l+r)>>1;
if(val[lc[p]]<x) return ask(l,mid,x,lc[p]);
else return ask(mid+1,r,x,rc[p]);
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),s[++s[0]]=a[i],s[++s[0]]=a[i]+1;
s[++s[0]]=0;
sort(s+1,s+s[0]+1);
s[0]=unique(s+1,s+s[0]+1)-s-1;
build(1,s[0],root[0]);
for(int i=1;i<=n;++i) insert(1,s[0],lower_bound(s+1,s+s[0]+1,a[i])-s,i,root[i],root[i-1]);
for(int i=1,L,R;i<=m;++i) scanf("%d %d",&L,&R),printf("%d\n",ask(1,s[0],L,root[R]));
}
2.带修主席树(树状数组套线段树)
带修区间l~r中大于或小于k的数的个数。
前置知识
树状数组(外层),线段树(内层),主席树(建树方式)。
简述
对于一个长度为n的数组,加上所有修改值查询值进行离散化后,数值范围为1-s[0],则建n棵范围为s[0]的线段树。
区别于主席树的是,主席树是前后两棵树相关联,每棵树负责1-i的范围,而树状数组套线段树是按树状数组的方式按2i进行前后树的关联,每棵树负责的范围按树状数组的i负责的范围计算。
则我们计算答案时只需要:
calc(r,k)-calc(l-1,k);
int calc(int x,int k)
{
int res=0;
for(;x;x-=x&-x) res+=ask(1,s[0],k,root[x]);
return res;
}
//ask中是否取等号由题目决定
注意:
1.每棵线段树相对独立毫无关联
2.查询操作包括:找需要用的线段树,普通线段树判断进入左右子树,判断每棵线段树左右子树是否存在,如果存在就加入cur数组。(减少多余计算)
代码分别为:
int query(int x)
{
cur1[0]=cur2[0]=0;
for(int i=q[x].r;i;i-=i&-i) cur1[++cur1[0]]=root[i];
for(int i=q[x].l-1;i;i-=i&-i) cur2[++cur2[0]]=root[i];
return ask(1,s[0],q[x].k);
}
二三合在一起:
int ask(int l,int r,int k)
{
if(l==r) return l;
int m=(l+r)/2,val=0;
for(int i=1;i<=cur1[0];++i) val+=t[t[cur1[i]].ls].val;
for(int i=1;i<=cur2[0];++i) val-=t[t[cur2[i]].ls].val;`
if(k<=val)
{
int len=cur1[0];
cur1[0]=0;
for(int i=1;i<=len;++i)
if(t[cur1[i]].ls) cur1[++cur1[0]]=t[cur1[i]].ls;
len=cur2[0];
cur2[0]=0;
for(int i=1;i<=len;++i)
if(t[cur2[i]].ls) cur2[++cur2[0]]=t[cur2[i]].ls;
return ask(l,m,k);
}
else
{
int len=cur1[0];
cur1[0]=0;
for(int i=1;i<=len;++i)
if(t[cur1[i]].rs) cur1[++cur1[0]]=t[cur1[i]].rs;
len=cur2[0];
cur2[0]=0;
for(int i=1;i<=len;++i)
if(t[cur2[i]].rs) cur2[++cur2[0]]=t[cur2[i]].rs;
return ask(m+1,r,k-val);
}
}
模板题:P2617
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,tt,a[N],root[N],s[N*2],cur1[N],cur2[N];
struct q_
{
int l,r,k;
}q[N];
struct t_
{
int ls,rs,val;
}t[N*400];
//要用这个区间就建不用就拉倒
void change(int l,int r,int x,int d,int &p)
{
if(!p) p=++tt;
t[p].val+=d;
if(l==r) return;
int m=(l+r)/2;
if(x<=m) change(l,m,x,d,t[p].ls);
else change(m+1,r,x,d,t[p].rs);
}
//树状数组添加
void add(int x,int d,int k)
{
for(;x<=n;x+=x&-x) change(1,s[0],k,d,root[x]);
}
int ask(int l,int r,int k)
{
if(l==r) return l;
int m=(l+r)/2,val=0;
for(int i=1;i<=cur1[0];++i) val+=t[t[cur1[i]].ls].val;
for(int i=1;i<=cur2[0];++i) val-=t[t[cur2[i]].ls].val;
if(k<=val)
{
int len=cur1[0];
cur1[0]=0;
for(int i=1;i<=len;++i)
if(t[cur1[i]].ls) cur1[++cur1[0]]=t[cur1[i]].ls;
len=cur2[0];
cur2[0]=0;
for(int i=1;i<=len;++i)
if(t[cur2[i]].ls) cur2[++cur2[0]]=t[cur2[i]].ls;
return ask(l,m,k);
}
else
{
int len=cur1[0];
cur1[0]=0;
for(int i=1;i<=len;++i)
if(t[cur1[i]].rs) cur1[++cur1[0]]=t[cur1[i]].rs;
len=cur2[0];
cur2[0]=0;
for(int i=1;i<=len;++i)
if(t[cur2[i]].rs) cur2[++cur2[0]]=t[cur2[i]].rs;
return ask(m+1,r,k-val);
}
}
//树状数组计算
//先求出有哪些树
int query(int x)
{
cur1[0]=cur2[0]=0;
for(int i=q[x].r;i;i-=i&-i) cur1[++cur1[0]]=root[i];
for(int i=q[x].l-1;i;i-=i&-i) cur2[++cur2[0]]=root[i];
return ask(1,s[0],q[x].k);
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),s[++s[0]]=a[i];
for(int i=1;i<=m;++i)
{
char op[5];
scanf("%s",&op);
if(op[0]=='Q') scanf("%d %d %d",&q[i].l,&q[i].r,&q[i].k);
else scanf("%d %d",&q[i].l,&q[i].k),s[++s[0]]=q[i].k;
}
sort(s+1,s+s[0]+1);
s[0]=unique(s+1,s+s[0]+1)-s-1;
for(int i=1;i<=n;++i) a[i]=lower_bound(s+1,s+s[0]+1,a[i])-s;
for(int i=1;i<=m;++i)
if(!q[i].r)
q[i].k=lower_bound(s+1,s+s[0]+1,q[i].k)-s;
for(int i=1;i<=n;++i) add(i,1,a[i]);
for(int i=1;i<=m;++i)
{
if(q[i].r) printf("%d\n",s[query(i)]);
else
{
add(q[i].l,-1,a[q[i].l]);
add(q[i].l,1,q[i].k);
a[q[i].l]=q[i].k;
}
}
}
3.树上主席树
其实很简单就是每个v以u为基础建一棵新树。
模板题:P4216
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,q,a[N];
int tq,qu[N],qv[N],qw[N];
int tt,root[N<<5],lc[N<<5],rc[N<<5],cnt[N<<5];
int fa[N],dep[N],siz[N],son[N],pre[N];
vector<int>vv[N];
void dfs1(int u)
{
siz[u]=1;
for(int i=0;i<vv[u].size();++i)
{
int v=vv[u][i];
dep[v]=dep[u]+1;
dfs1(v);
if(siz[v]>siz[son[u]]) son[u]=v;
siz[u]+=siz[v];
}
}
void insert(int l,int r,int x,int p1,int &p2)
{
cnt[p2=++tt]=cnt[p1]+1;
if(l==r) return;
int m=(l+r)>>1;
if(x<=m) insert(l,m,x,lc[p1],lc[p2]),rc[p2]=rc[p1];
else insert(m+1,r,x,rc[p1],rc[p2]),lc[p2]=lc[p1];
}
void dfs2(int u,int x)
{
pre[u]=x;
insert(1,q,a[u],root[fa[u]],root[u]);
if(!son[u]) return;
dfs2(son[u],x);
for(int i=0;i<vv[u].size();++i)
if(vv[u][i]!=son[u]) dfs2(vv[u][i],vv[u][i]);
}
int lca_(int u,int v)
{
while(pre[u]!=pre[v])
{
if(dep[pre[u]]<dep[pre[v]]) swap(u,v);
u=fa[pre[u]];
}
return dep[u]<dep[v]?u:v;
}
int ask(int l,int r,int x,int p1,int p2,int p3)
{
if(x<=0) return 0;
if(l==r) return cnt[p1]+cnt[p2]-cnt[p3]*2;
int m=(l+r)>>1;
if(x<=m) return ask(l,m,x,lc[p1],lc[p2],lc[p3]);
else return cnt[lc[p1]]+cnt[lc[p2]]-cnt[lc[p3]]*2+ask(m+1,r,x,rc[p1],rc[p2],rc[p3]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&fa[i]),vv[fa[i]].push_back(i);
scanf("%d",&q);
for(int i=1;i<=n;++i) a[i]=q;
for(int i=1,op,x;i<=q;++i)
{
scanf("%d",&op);
if(op==1) ++tq,scanf("%d %d %d",&qu[tq],&qv[tq],&qw[tq]),qw[tq]=i-qw[tq]-1;
else scanf("%d",&x),a[x]=i;
}
dfs1(vv[0][0]);
dfs2(vv[0][0],vv[0][0]);
for(int i=1;i<=tq;++i)
{
int lca=lca_(qu[i],qv[i]);
// cout<<qw[i]<<" ";
printf("%d %d\n",dep[qu[i]]+dep[qv[i]]-dep[lca]*2+1,ask(1,q,qw[i],root[qu[i]],root[qv[i]],root[lca])+(a[lca]<=qw[i]));
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号