线段树

即对数组进行二分保存。

由图易得，除去最后一层，树的深度为\(log\)₂\(N\)，则树的大小约为\(N*2\)≤2⁰+2¹+2²+……+2^log2N/2<\(N*4\)，但在一些特殊的图上，可能会大于\(N*4\)，所以一般而言，线段树数组开到N*8的大小。

主要操作

1.单点修改

注意左右节点和父节点之间的传递关系。

以区间和为例。

一般子节点和父节点进行传递时，会额外建立一个\(update(int p)\)函数，避免重复写时出错，本样例比较简单，所以没有进行额外建立。

建立

struct tree
{
    int l,r,val;
}t[N<<3];
void build(int l,int r,int p)
{
    if（l==r)
   	{
        t[p]=(tree){l,r,a[l]};
        return;
   	}
    
    int m=(l+r)/2;
    build(l,m,p*2);
    build(m+1,r,p*2+1);
    
    t[p]=(tree){l,r,max(t[p*2],t[p*2+1])};
}

查询

int ask(int l,int r,int p)
{
    if(t[p].l>=l&&t[p].r<=r) return t[p].val;
    
    int m=(t[p].l+t[p].r)/2,vall=-INF,valr=-INF;
    if(l<=m) vall=ask(l,r,p*2);
    if(r>m) valr=ask(l,r,p*2+1);
    
    return max(vall,valr);
}

修改

void change(int x,int val,int p)
{
    if(t[p].l==t[p].r)
    {
        t[p].val=val;
        return;
    }
    int m=(t[p].l+t[p].r)/2;
    if(x<=m) change(x,val,p*2);
    else change(x,val,p*2+1);
    
    t[p].val=max(t[p*2].val,t[p*2+1].val);
}

【JSOI 2008】最大数

【题目描述】
给定一个正整数数列 a1,a2,a3,⋯,an ，每一个数都在 0∼p–1 之间。可以对这列数进行两种操作：

添加操作：向序列后添加一个数，序列长度变成 n+1；

询问操作：询问这个序列中最后 L 个数中最大的数是多少。

程序运行的最开始，整数序列为空。写一个程序，读入操作的序列，并输出询问操作的答案。

【数据输入】
第一行有两个正整数 m,p，意义如题目描述；

接下来 m 行，每一行表示一个操作。如果该行的内容是 Q L，则表示这个操作是询问序列中最后 L 个数的最大数是多少；如果是 A t，则表示向序列后面加一个数，加入的数是 (t+a)modp。其中，t 是输入的参数，a 是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 a=0）。

第一个操作一定是添加操作。对于询问操作，L>0 且不超过当前序列的长度。

【数据输出】
对于每一个询问操作，输出一行。该行只有一个数，即序列中最后 L 个数的最大数。

【输入样例】
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99

【输出样例】
97
97
97
60
60
97

#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5;
int n,p,tot;
struct t_
{
	int l,r,val;	
}t[N<<3];

void build(int l,int r,int p)
{
	t[p]=(t_){l,r,0};
	
	if(l==r) return;
	
	int m=(l+r)/2;
	build(l,m,p*2);
	build(m+1,r,p*2+1);
}

void change(int x,int val,int p)
{
	if(t[p].l==t[p].r)
	{
		t[p].val=val;
		return;
	}
	
	int m=(t[p].l+t[p].r)/2;
	change(x,val,p*2+(x>m));
	
	t[p].val=max(t[p*2].val,t[p*2+1].val);
}

int ask(int l,int r,int p)
{
	if(t[p].l>=l&&t[p].r<=r) return t[p].val;
	
	int ans=0,m=(t[p].l+t[p].r)/2;
	
	if(l<=m) ans=ask(l,r,p*2);
	if(r>m) ans=max(ans,ask(l,r,p*2+1));
	
	return ans;
}
int main()
{
	scanf("%d %d",&n,&p);
	
	build(1,n,1);
	
	char op[2];
	int x,y=0;
	while(n--)
	{
		scanf("%s %d",&op,&x);
		if(op[0]=='A') change(++tot,(y+x)%p,1);
		else printf("%d\n",y=ask(tot-x+1,tot,1));
	}
	
}

你能回答这些问题吗

给定长度为N的数列A，以及M条指令，每条指令可能
是以下两种之一：

1、“1 x y”，查询区间 [x,y] 中的最大连续子段和，
即 maxx≤l≤r≤y{∑ri=lA[i]}。

2、“2 x y”，把 A[x] 改成 y。

对于每个查询指令，输出一个整数表示答案。

输入格式
第一行两个整数N,M。

第二行N个整数A[i]。

接下来M行每行3个整数k,x,y，k=1表示查询（此时如
果x>y，请交换x,y），k=2表示修改。

输出格式
对于每个查询指令输出一个整数表示答案。

每个答案占一行。

数据范围
N≤500000,M≤100000
输入样例：

输出样例：

对于每个区间，储存最大值，左边界连续最大值，右边界连续最大值。

对于每个节点p：

\[t[p].dat=max(max(t[p*2].dat,t[p*2+1].dat),t[p*2].rmax+t[p*2+1].lmax) \]

\[t[p].sum=t[p*2].sum+t[p*2+1].sum; \]

\[t[p].lmax=max(t[p*2].lmax,t[p*2].sum+t[p*2+1].lmax); \]

\[t[p].rmax=max(t[p*2+1].rmax,t[p*2+1].sum+t[p*2].rmax) \]

#include<bits/stdc++.h>
using namespace std;
#define N 500005
#define INF 0x3fffffff
int n,m,a[N];
struct tree
{
	int l,r,dat,sum,lmax,rmax;
}t[N<<2];
//l r ans sum(l~r) lmax rmax

void update(int p)
{
	t[p].dat=max(max(t[p*2].dat,t[p*2+1].dat),t[p*2].rmax+t[p*2+1].lmax);
	t[p].sum=t[p*2].sum+t[p*2+1].sum;
	t[p].lmax=max(t[p*2].lmax,t[p*2].sum+t[p*2+1].lmax);
	t[p].rmax=max(t[p*2+1].rmax,t[p*2+1].sum+t[p*2].rmax);
}
void build(int l,int r,int p)
{
	if(l==r) 
	{          
		t[p]=(tree){l,r,a[l],a[l],a[l],a[l]};
		return;
	}
	
	int m=(l+r)/2;
	build(l,m,p*2);
	build(m+1,r,p*2+1);
	
	t[p].l=l;
	t[p].r=r;
	update(p);
}

tree ask(int l,int r,int p)
{
	if(l<=t[p].l&&r>=t[p].r) return t[p];
	
	int m=(t[p].l+t[p].r)/2;
	tree a,b,c;
	a=b=(tree){0,0,-INF,-INF,-INF,-INF};
	c.sum=0;
	
	if(l<=m) a=ask(l,r,p*2),c.sum+=a.sum;//left tree
	if(r>m)  b=ask(l,r,p*2+1),c.sum+=b.sum;
	
	c.dat=max(max(a.dat,b.dat),a.rmax+b.lmax);

	c.lmax=max(a.lmax,b.lmax+a.sum);
	if(l>m) c.lmax=max(c.lmax,b.lmax);
	
	c.rmax=max(b.rmax,b.sum+a.rmax);
	if(r<=m) c.rmax=max(c.rmax,a.rmax);
	
	return c; 
	
}

void change(int x,int y,int p)
{
	if(t[p].l==t[p].r)
	{
		t[p]=(tree){x,x,y,y,y,y};
		return;
	}
	int m=(t[p].l+t[p].r)/2;
	
	change(x,y,p*2+(x>m));
	
	update(p);
}

int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;++i)
	scanf("%d",&a[i]);
	build(1,n,1); 
	int k,x,y;
	while(m--)
	{
		scanf("%d %d %d",&k,&x,&y);
		if(k==1)
		{
			if(x>y) swap(x,y);
			printf("%d\n",ask(x,y,1).dat);
		}
		else change(x,y,1);
	}
	return 0;
}

区间最大公约数

给定一个长度为N的数列A，以及M条指令，每条指令可能
是以下两种之一：

1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。

2、“Q l r”，表示询问 A[l],A[l+1],…,A[r] 的最大
公约数(GCD)。

对于每个询问，输出一个整数表示答案。

输入格式
第一行两个整数N,M。

第二行N个整数A[i]。

接下来M行表示M条指令，每条指令的格式如题目描述所示。

输出格式
对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围
N≤500000,M≤100000
输入样例：

输出样例：

1
2
4

由\(gcd(x,y)=gcd(x,x-y)=gcd(x-y,y)\)可推出\(gcd(x,y,z)=gcd(x-y,x-z,y-z)\)成立，由归纳法易得有n个数时该定理也成立。

由以上定理可知，可建立一个线段树储存区间l~r的最大公约数，特殊地，当\(l==r\)时，公约数为\(num[l]--num[l-1]\)。

每次修改L~R时，区间内差值不变，L与其前的差值增加d，但R+1处需要把D减去，这样到区间横跨L，R时对\(gcd()\)无影响，当区间经过L或者R时，\(gcd()\)会有更新，\(+d\)和\(-d\)在\(gcd()\)运算时等价。

每次查询时，查询L+1到R的最大公约数与\(now[L]\)进行\(gcd()\)运算的值。

为了快速得到\(now[L]\)的值，我们需要额外建立一个树状数组保存修改值。

#include<bits/stdc++.h>
using namespace std;
#define maxn 500005
int n,m;
long long num[maxn],b[maxn];
struct
{
	int l,r;
	long long g;
}t[maxn<<2];

long long build(int p,int l,int r)
{
	t[p].l=l;
	t[p].r=r;
	if(l==r) t[p].g=num[l]-num[l-1];
	else
	{
		int m=(l+r)/2;
		t[p].g=__gcd(build(p*2,l,m),build(p*2+1,m+1,r));
	}
	return t[p].g;
}

long long ask(int p,int l,int r)
{
	if(l>r) return 0;
	if(t[p].l>=l&&t[p].r<=r) return abs(t[p].g);
	
	long long a=0,b=0;
	int m=(t[p].l+t[p].r)/2;
	if(l<=m) a=ask(p*2,l,r);
	if(r>m) b=ask(p*2+1,l,r);
	
	return abs(__gcd(a,b));
}

void add(int p,int x,long long y)
{
	if(x>n) return;
	if(t[p].l==t[p].r) t[p].g+=y;
	else
	{
		int m=(t[p].l+t[p].r)/2;
		
		if(x<=m) add(p*2,x,y);
		else add(p*2+1,x,y);
		
		t[p].g=__gcd(t[p*2].g,t[p*2+1].g);
	}
	return;
}

void aadd(int x,long long d)
{
	for(;x<=n;x+=x&-x) b[x]+=d;
}

long long aask(int x)
{
	long long ans=0;
	for(;x;x-=x&-x) ans+=b[x];
	return ans;
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&num[i]);
	build(1,1,n);
	
	while(m--)
	{
		char op[2];
		int l,r;
		scanf("%s %d %d",&op,&l,&r);
		if(l>r) swap(l,r);
		
		if(op[0]=='Q') printf("%lld\n",__gcd(num[l]+aask(l),ask(1,l+1,r)));
		else
		{
			long long d;
			scanf("%lld",&d);
			
			add(1,l,d);
			aadd(l,d);
			if(r+1<=n)
			{
				add(1,r+1,-d);
				aadd(r+1,-d);
			}
		}
		
//		for(int i=1;i<=10;i++) cout<<t[i].g<<" ";
//		cout<<endl<<endl;
	}
	return 0;
}

2.区间修改

以区间和为例。

1.转化为单点修改。

区间外枚举单点

void change(int x,int val,int p)
{
    if(t[p].l==t[p].r)
    {
        t[p].val=val;
        return;
    }
    int m=(t[p].l+t[p].r)/2;
    if(x<=m) change(x,val,p*2);
    else change(x,val,p*2+1);
    
    t[p].val=t[p*2].val+t[p*2+1].val;
}

while(l<=r) change(l,val,p);

区间内进行单点修改

void change(int l,int r,int val,int p)
{
    if(t[p].l==t[p].r)
    {
        t[p].val+=val;
        return;
    }
    
    int m=(t[p].l+t[p].r)/2;
    if(l<=m) change(l,r,val,p*2);
    if(r>m) change(l,r,val,p*2+1);
    
    t[p].val=t[p*2].val+t[p*2+1].val;
}

2.延迟标记

延迟标记会覆盖某一区间，只有当取用区间内的值时，才会将标记下传，修改子区间的值。由于其本身不进行多余的修改操作，并在被修改时直接对某一区间进行覆盖，比精确到每一个点的修改更加高效。

在解决区间修改单点查询的问题时，我们一般选用树状数组，因为树状数组查询单点的前缀和效率非常高。

但在解决区间修改区间查询的问题时，我们一般选用使用线段树，因为线段树更直观更简单，需要的数学水平更低，更适合初学者。

延迟标记会新建立一个变量，记录区间t[p].l~t[p].r每个单点被共同修改的值，在使用子区间时标记下传。

下传

void spread(int p)
{
	if(!t[p].add) return;
	t[p*2].add+=t[p].add;
	t[p*2].ans+=t[p].add*(t[p*2].r-t[p*2].l+1);
	t[p*2+1].add+=t[p].add;
	t[p*2+1].ans+=t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
	t[p].add=0;
}

建立

struct tree
{
    int l,r,add,cnt;
}t[N<<3];
void build(int l,int r,int p)
{
    if（l==r)
   	{
        t[p]=(tree){l,r,0,a[l]};
        return;
   	}
    
    int m=(l+r)/2;
    build(l,m,p*2);
    build(m+1,r,p*2+1);
    
    t[p]=(tree){l,r,0,a[p*2].val+a[p*2+1].val};
}

查询

int ask(int l,int r,int p)
{
    if(t[p].l>=l&&t[p].r<=r) return t[p].val;
    
    spread(p);
    int m=(t[p].l+t[p].r)/2,vall=0,valr=0;
    if(l<=m) vall=ask(l,r,p*2);
    if(r>m) valr=ask(l,r,p*2+1);
    
    return vall+valr;
}

修改

void change(int p,int l,int r,int d)
{
	if(t[p].l>=l&&t[p].r<=r)
	{
		t[p].add+=d;
		t[p].ans+=d*(t[p].r-t[p].l+1);
	}
	else
	{
		spread(p);
		int m=(t[p].l+t[p].r)/2;
		
		if(l<=m) change(p*2,l,r,d);
		if(r>m) change(p*2+1,l,r,d);
		
		t[p].ans=t[p*2].ans+t[p*2+1].ans;
	}
	
	return;
}

一个简单的整数问题2

给定一个长度为N的数列A，以及M条指令，每条指令可能是以下两种之一：

1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。

2、“Q l r”，表示询问数列中第 l~r 个数的和。

对于每个询问，输出一个整数表示答案。

输入格式
第一行两个整数N,M。

第二行N个整数A[i]。

接下来M行表示M条指令，每条指令的格式如题目描述所示。

输出格式
对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围
1≤N,M≤105,
|d|≤10000,
|A[i]|≤1000000000
输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

输出样例：

#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
int n,m;
long long num[maxn];
struct
{
	int l,r;
	long long add,ans;
}t[maxn*4];

void spread(int p)
{
	if(!t[p].add) return;
	t[p*2].add+=t[p].add;
	t[p*2].ans+=t[p].add*(t[p*2].r-t[p*2].l+1);
	t[p*2+1].add+=t[p].add;
	t[p*2+1].ans+=t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
	t[p].add=0;
}

void build(int p,int l,int r)
{
	t[p].l=l;
	t[p].r=r;
	if(l==r) t[p].ans=num[l];
	else
	{
		int m=(l+r)/2;
		build(p*2,l,m);
		build(p*2+1,m+1,r);
		t[p].ans=t[p*2].ans+t[p*2+1].ans;
	}
	return;
}

long long ask(int p,int l,int r)
{
	if(t[p].l>=l&&t[p].r<=r) return t[p].ans;
	
	spread(p);
	
	int m=(t[p].l+t[p].r)/2;
	long long ans=0;
	if(l<=m) ans+=ask(p*2,l,r);
	if(r>m) ans+=ask(p*2+1,l,r);
	
	return ans;
}

void change(int p,int l,int r,long long d)
{
	if(t[p].l>=l&&t[p].r<=r)
	{
		t[p].add+=d;
		t[p].ans+=(long long)d*(t[p].r-t[p].l+1);
	}
	else
	{
		spread(p);
		int m=(t[p].l+t[p].r)/2;
		
		if(l<=m) change(p*2,l,r,d);
		if(r>m) change(p*2+1,l,r,d);
		
		t[p].ans=t[p*2].ans+t[p*2+1].ans;
	}
	
	return;
}

int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&num[i]);
	build(1,1,n);
	while(m--)
	{
		char op[2];
		int l,r;
		scanf("%s %d %d",&op,&l,&r);
		if(op[0]=='Q') printf("%lld\n",ask(1,l,r));
		else
		{
			long long d;
			scanf("%lld",&d);
			change(1,l,r,d);
		}
	}
}

【BZOJ 3211】花神游历各国

Output
每次x=1时，每行一个整数，表示这次旅行的开心度

Sample Input

Sample Output

HINT
对于100%的数据， n ≤ 100000，m≤200000 ,data[i]非负且小于10^9

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+5;
ll n,m,a[N];
struct
{
	ll l,r,flag,val;
}t[N<<3];

inline ll read()
{
	char dd;
	ll res=0,w=1;
	while((dd=getchar())&&(dd>'9'||dd<'0'))
		if(dd=='-') w=-1;
	res=dd-'0';
	while((dd=getchar())&&dd<='9'&&dd>='0') res=res*10+dd-'0';
	return res;
}

void build(ll l,ll r,ll p)
{
	t[p].l=l;
	t[p].r=r;
	if(l==r)
	{
		t[p].val=a[l];
		t[p].flag=(t[p].val<=1);
		return;
	}
	
	ll m=(l+r)/2;
	
	build(l,m,p*2);
	build(m+1,r,p*2+1);
	
	t[p].val=t[p*2].val+t[p*2+1].val;
	t[p].flag=t[p*2].flag&t[p*2+1].flag;
}
ll ask(ll l,ll r,ll p)
{
	if(t[p].l>=l&&t[p].r<=r) return t[p].val;
	
	ll ans=0,m=(t[p].l+t[p].r)/2;
	
	if(l<=m) ans+=ask(l,r,p*2);
	if(r>m) ans+=ask(l,r,p*2+1);
	
	return ans;
}

void change(ll l,ll r,ll p)
{
	if(t[p].flag) return;
	if(t[p].l==t[p].r)
	{
		t[p].val=sqrt(t[p].val);
		t[p].flag=(t[p].val<=1);
		return;
	}
	
	ll m=(t[p].l+t[p].r)/2;
	if(l<=m) change(l,r,p*2);
	if(r>m) change(l,r,p*2+1);
	
	t[p].val=t[p*2].val+t[p*2+1].val;
	t[p].flag=t[p*2].flag&t[p*2+1].flag;
}

int main()
{
	n=read();
	for(ll i=1;i<=n;++i) a[i]=read();
	build(1,n,1);
	
	m=read();
	
	
	ll x,l,r;
	
	while(m--)
	{
		x=read();l=read();r=read();
		if(l>r) swap(l,r);
		if(x==1) printf("%lld\n",ask(l,r,1));
		else change(l,r,1);
	}
}

【AHOI】维护序列

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+5;
ll n,m,pt,a[N];
struct t_
{
	ll l,r,add,mul,val;
}t[N<<3];

inline ll read()
{
	char dd;
	ll res;
	while((dd=getchar())&&(dd>'9'||dd<'0'));
	res=dd-'0';
	while((dd=getchar())&&dd<='9'&&dd>='0') res=res*10+dd-'0';
	return res;
}

inline void update(ll p)
{
	t[p].val=(t[p*2].val+t[p*2+1].val)%pt;
}
inline void spread_add(ll p)
{
	if(!t[p].add) return;
	
	ll &x=t[p].add;
	t_ &l=t[p*2],&r=t[p*2+1];
	
	l.add=(l.add+x)%pt;
	r.add=(r.add+x)%pt;
	
	l.val=(ll)(l.val+(l.r-l.l+1)*x)%pt;
	r.val=(ll)(r.val+(r.r-r.l+1)*x)%pt;
	x=0;
}
inline void spread_mul(ll p)
{
	if(t[p].mul==1) return;
	
	ll &x=t[p].mul;
	t_ &l=t[p*2],&r=t[p*2+1];
	
	l.mul=(ll)(l.mul*x)%pt;
	r.mul=(ll)(r.mul*x)%pt;
	
	l.add=(ll)(l.add*x)%pt;
	r.add=(ll)(r.add*x)%pt;
	
	l.val=(ll)(l.val*x)%pt;
	r.val=(ll)(r.val*x)%pt;
	
	x=1;
}
void build(ll l,ll r,ll p)
{
	t[p].l=l;
	t[p].r=r;
	t[p].add=0;
	t[p].mul=1;
	if(l==r)
	{
		t[p].val=a[l];
		return;
	}
	ll m=(l+r)/2;
	build(l,m,p*2);
	build(m+1,r,p*2+1);
	
	update(p);
}

void add_(ll l,ll r,ll val,ll p)
{
	if(t[p].l>=l&&t[p].r<=r)
	{
		t[p].add=(t[p].add+val)%pt;
		t[p].val=(t[p].val+(ll)(t[p].r-t[p].l+1)*val%pt)%pt;
		return;
	}
	
	spread_mul(p);	
	spread_add(p);

	
	ll m=(t[p].l+t[p].r)/2;
	if(l<=m) add_(l,r,val,p*2);
	if(r>m) add_(l,r,val,p*2+1);
	
	update(p);
}

void mul_(ll l,ll r,ll val,ll p)
{
	if(t[p].l>=l&&t[p].r<=r)
	{
		t[p].add=(ll)(t[p].add*val)%pt;
		t[p].mul=(ll)(t[p].mul*val)%pt;
		t[p].val=(ll)(t[p].val*val)%pt;
		return;
	}
	
	spread_mul(p);	
	spread_add(p);

	
	ll m=(t[p].l+t[p].r)/2;
	if(l<=m) mul_(l,r,val,p*2);
	if(r>m) mul_(l,r,val,p*2+1);
	
	update(p);
}

ll ask(ll l,ll r,ll p)
{
	if(t[p].l>=l&&t[p].r<=r) return t[p].val;

	spread_mul(p);	
	spread_add(p);
	
	ll ans=0,m=(t[p].l+t[p].r)/2;
	
	if(l<=m) ans=(ans+ask(l,r,p*2))%pt;
	if(r>m) ans=(ans+ask(l,r,p*2+1))%pt;
	
	return ans;
}
int main()
{
	n=read();pt=read();
	for(ll i=1;i<=n;++i) a[i]=read()%pt;
	
	build(1,n,1);
	m=read();
	
	ll op,l,r,x;
	while(m--)
	{
		op=read();l=read();r=read();
		switch(op)
		{
			case 1:x=read()%pt;mul_(l,r,x,1);break;
			case 2:x=read()%pt;add_(l,r,x,1);break;
			case 3:printf("%d\n",ask(l,r,1));break;
		}
	}
}

3.标记永久化

标记永久化的原理简单来说就是修改时一路更改被影响到的点，询问时则一路累加路上的标记，从而省去下传标记的操作。

3.扫描线

即将一个由多个规则矩形重叠形成不规则的矩形用一条线从左到右或者从上到下进行扫描，人为的分为N块不相互重叠的规则矩形。

线段树保存某一段被覆盖的次数，以及该区间内被覆盖的长度。

对于初始的规则矩形，以从左到右扫描为例，\((x1,y1)\)为左上角，\((x2,y2)\)为右上角，则记录边\(e(x1,y1,y2,1),e(x1,y1,y2,-1)\)，其中1表示将此边加入，-1表示将此边删除。

将边按x的值进行排序，每次扫描到一个新的x时，会进行两个操作：

1.更新答案：\(ans+=(line[i].x-line[i-1].x)*t[1].len\)

2.修改操作：\(change(1,lsh[line[i].l],lsh[line[i].r]-1,line[i].state)\)

要根据具体题意决定两者的操作顺序，如例题亚特兰蒂斯就是先更新答案再修改，而例题窗外的星星却是先修改再更新答案。

下面将以亚特兰蒂斯为例进行更为仔细地讲解。

亚特兰蒂斯

有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。

其中一些甚至包括岛屿部分地图。

但不幸的是，这些地图描述了亚特兰蒂斯的不同区域。

您的朋友Bill必须知道地图的总面积。

你自告奋勇写了一个计算这个总面积的程序。

输入格式
输入包含多组测试用例。

对于每组测试用例，第一行包含整数n，表示总的地图数量。

接下来n行，描绘了每张地图，每行包含四个数字x1,y1,x2,y2（不一定是整数）,(x1,y1)和(x2,y2)分别是地图的左上角位置和右下角位置。

注意，坐标轴 x 轴从上向下延伸，y 轴从左向右延伸。

当输入用例n=0时，表示输入终止，该用例无需处理。

输出格式
每组测试用例输出两行。

第一行输出”Test case #k”，其中k是测试用例的编号，
从1开始。

第二行输出“Total explored area: a”，其中a是总地
图面积（即此测试用例中所有矩形的面积并，注意如果一
片区域被多个地图包含，则在计算总面积时只计算一次），
精确到小数点后两位数。

在每个测试用例后输出一个空行。

数据范围
1≤n≤10000,
0≤x1<x2≤100000,
0≤y1<y2≤100000
注意，本题 n 的范围上限加强至 10000。

输入样例：

2
10 10 20 20
15 15 25 25.5
0

输出样例：

Test case #1
Total explored area: 180.00

题目给了n个矩形，每个矩形给了左下角和右上角的坐标，矩形可能会重叠，求的是矩形最后的面积。因为变化范围比较大，我们要用到离散化，离散化就不说了，重点说一说扫描线的过程：

现在假设我们有一根线，从下往上开始扫描

我们可以把整个矩形分成如图各个颜色不同的小矩形，那么这个小矩形的高就是我们扫过的距离，那么剩下了一个变量，那就是矩形的长一直在变化。

我们的线段树就是为了维护矩形的长，我们给每一个矩形的上下边进行标记，下面的边标记为1，上面的边标记为-1，每遇到一个矩形时，我们知道了标记为1的边，我们就加进来这一条矩形的长，等到扫描到-1时，证明这一条边需要删除，就删去，利用1和-1可以轻松的到这种状态。

还要注意这里的线段树指的并不是线段的一个端点，而指的是一个区间，所以我们要计算的时候r+1和r-1。

#include<bits/stdc++.h>
using namespace std;
#define maxn 200005
int n,tot,tt;
double ny[maxn];
struct op
{
	double x;
	double l,r;
	int state;
}line[maxn];
struct
{
	int l,r;
	int cover;
	double len;
}t[maxn*8];

void add(double a,double b,double c,double d,int e)
{
	line[++tt].x=a;
	line[tt].l=b;
	line[tt].r=c;
	line[tt].state=e;
	ny[tt]=d;
}

bool cmp(op a,op b)
{
	return a.x<b.x;
}

void han(int p)
{
	t[p].len=t[p].cover?(ny[t[p].r+1]-ny[t[p].l]):(t[p*2].len+t[p*2+1].len);
}

void build(int p,int l,int r)
{
	t[p].l=l;
	t[p].r=r;
	t[p].cover=0;
	if(l==r) t[p*2].len=t[p*2+1].len=0;
	else
	{
		int m=(l+r)/2;
		build(p*2,l,m);
		build(p*2+1,m+1,r);
	}
	han(p);
	return;
}

void change(int p,int l,int r,int d)
{
	if(t[p].l>=l&&t[p].r<=r) t[p].cover+=d;
	
	else
	{
		int m=(t[p].l+t[p].r)/2;
		if(l<=m) change(p*2,l,r,d);
		if(r>m) change(p*2+1,l,r,d);
	}
	han(p);
//	cout<<p<<" "<<t[p].l<<" "<<t[p].r<<" "<<t[p].add<<" "<<t[p].cover<<" "<<t[p].len<<"\n";
	return;
}
int main()
{
	while(scanf("%d",&n)&&n)
	{
		tt=0;
		for(int i=1;i<=n;i++)
		{
			double a,b,c,d;
			scanf("%lf %lf %lf %lf",&a,&b,&c,&d);
			if(a==c&&b==d) continue;
			add(a,b,d,b,1);
			add(c,b,d,d,-1);
		}
		
		
		int ty=tt;
		map<double,int>pre;
		
		sort(ny+1,ny+tt+1);
		tt=unique(ny+1,ny+tt+1)-(ny+1);
		for(int i=1;i<=tt;i++) pre[ny[i]]=i;
		ny[tt+1]=ny[tt];
	
		build(1,1,tt);
		
		double ans=0;
		sort(line+1,line+ty+1,cmp);
//		printf("ty=%d\n",ty);
		for(int i=1;i<=ty;i++)
		{
//			printf("%lf %lf %lf %ld",line[i].x,line[i-1].x,t[1].len,ans);
			ans+=(line[i].x-line[i-1].x)*t[1].len;
			change(1,pre[line[i].l],pre[line[i].r]-1,line[i].state);
//			printf("%.2lf %.2lf %.2lf %.2lf\n\n",line[i].x,line[i-1].x,t[1].len,ans);
		}
		
		printf("Test case #%d\nTotal explored area: %.2lf\n\n",++tot,ans);
	}
	
	
}

窗内的星星

在一个天空中有很多星星（看作平面直角坐标系），已知每颗星星的坐标和亮度（都是整数）。

求用宽为W、高为H的矩形窗口（W,H为正整数）能圈住的星星的亮度总和最大是多少。（矩形边界上的星星不算）

输入格式
输入包含多组测试用例。

每个用例的第一行包含3个整数：n，W，H，表示星星的数量，矩形窗口的宽和高。

然后是n行，每行有3个整数：x，y，c，表示每个星星的位置（x，y）和亮度。

没有两颗星星在同一点上。

输出格式
每个测试用例输出一个亮度总和最大值。

每个结果占一行。

数据范围
1≤n≤10000,
1≤W,H≤1000000,
0≤x,y<231
输入样例：

输出样例：

5
6

首先将问题转化为:平面上由若干个区域,每个区域都带有一个权值,求在哪个坐标上重叠的区域权值和最大.记住,每一个区域都是有一个星星产生的,权值等于星星的亮度.
左上角,左下角,右上角,右下角可以由四元组保存\((x,y,y+h−1,c)(x,y,y+h−1,c)和(x+w,y,y+h−1,−c)(x+w,y,y+h−1,−c)\)然后按照横坐标第一位的值排序即可.四元组要分开看.\((x,y,c)(x,y,c)(x,y+h−1,c)(x,y+h−1,c)和(x+w,y)(x+w,y)(x+w,y+h−1,−c)\)

#include <bits/stdc++.h>
using namespace std;
const int N=2e4+10;//要2*n,切记切记,我就是因为这个恶心的锅,坑害了一个半小时.
#define int long long//注意
int n,w,h,ys[N];
struct line_tree
{
    int l,r,len,lazy;//开了懒惰标记,也就是延迟标记
} t[N<<2];
struct node
{
    int x,y1,y2,f;
} p[N];
int cmp(node a,node b)
{
    return a.x<b.x || (a.x==b.x && a.f<0);//排序特殊点
}
inline void push_up(int p)
{
    t[p].len=max(t[p*2].len,t[p*2+1].len)+t[p].lazy;
}
inline void build(int l,int r,int p)
{
	t[p]=(line_tree){ys[l],ys[r],0,0};
    if (r-l==1)
        return ;
    int m=(l+r)/2;
    build(l,m,p*2);
    build(m,r,p*2+1);
    push_up(p);
}
inline void change(int l,int r,int k,int p)
{
    if (t[p].l>=l && t[p].r<=r)
    {
        t[p].lazy+=k;
        t[p].len+=k;
        return ;
    }
    if (l<t[p*2].r)
        change(l,min(r,t[p*2].r),k,p*2);
    if (r>t[p*2+1].l)
        change(max(l,t[p*2+1].l),r,k,p*2+1);
    push_up(p);
}
inline void init()
{
    while(scanf("%lld%lld%lld",&n,&w,&h)!=EOF)
    {
        int cnt=0,num=1;
        for(int i=1; i<=n; i++)
        {
            int xx,yy,k;
            scanf("%lld%lld%lld",&xx,&yy,&k);
            p[cnt++]=(node){xx,yy,yy+h,k};
            p[cnt++]=(node){xx+w,yy,yy+h,-k};
            ys[num++]=yy;
            ys[num++]=yy+h;
        }
        sort(ys+1,ys+num);
        int ans=0;
        num=unique(ys+1,ys+num)-(ys+1);
        
        sort(p,p+cnt,cmp);
        build(1,num,1);
        for(int i=0; i<cnt; i++)
        {
            change(p[i].y1,p[i].y2,p[i].f,1);
                ans=max(ans,t[1].len);
        }
        printf("%lld\n",ans);
    }
}
signed main()
{
	init();
    return 0;
}

圆的扫描线

一篇很好的讲解

#include<bits/stdc++.h>
using namespace std;
#define x(i) cir[i].x
#define y(i) cir[i].y
#define r(i) cir[i].r
const int N=5e4+5;
int n,tot,ans[N];
double now;
struct cir_{double x,y,r;}cir[N];
struct line_ 
{
	double x,y;int id,op; 
	friend bool operator<(line_ a,line_ b)
	{
		return a.x!=b.x?a.x<b.x:a.y>b.y; 
	}
}li[N<<1];
struct node
{
	int id,op;
	double Y()
	{
		return y(id)+op*sqrt(r(id)*r(id)-(now-x(id))*(now-x(id)));
	}
	
	friend bool operator<(node a,node b)
	{
		double ay=a.Y(),by=b.Y();
		return ay!=by?ay>by:a.op>b.op;
	}
};
set<node>S;
set<node>::iterator it,pre,nxt;

int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	{
		scanf("%lf %lf %lf",&x(i),&y(i),&r(i));
		li[++tot]=(line_){x(i)-r(i),y(i),i,1};
		li[++tot]=(line_){x(i)+r(i),y(i),i,-1};
	} 
	
	sort(li+1,li+tot+1);
	for(int i=1;i<=tot;++i)
	{
		if(li[i].op==-1)
		{
			S.erase((node){li[i].id,1});
			S.erase((node){li[i].id,-1});
		}
		else
		{
			now=x(li[i].id);
			pre=nxt=it=S.insert((node){li[i].id,1}).first;
			pre--;nxt++;
			if(it==S.begin()||nxt==S.end()) ans[it->id]=1;
			else
			{
				if(pre->id==nxt->id) ans[it->id]=ans[pre->id]+1;
				else ans[it->id]=max(ans[pre->id],ans[nxt->id]);
			}
		}
		S.insert((node){li[i].id,-1});
	}
	int mx;
	for(int i=1;i<=n;++i) mx=max(mx,ans[i]);
	printf("%d",mx);
}

4.二维线段树（矩形四分）

二维数列的修改查询。

分法举例：

原图

经过一次划分后：

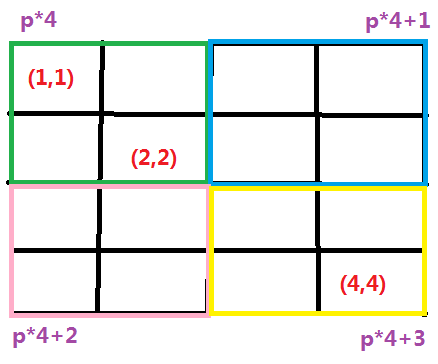
由于要多开四倍，所以空间浪费非常大，建议动态开点。

（十分钟速打的敷衍模板。）

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+5;
int n,m,k,a[N][N];
struct t_
{
	int l1,r1,l2,r2,val,add;
}t[N*N*16];

void build(int l1,int r1,int l2,int r2,int p)
{

	t[p]={l1,r1,l2,r2,0,0};
	
	if(l1==l2&&r1==r2)
	{
		t[p].val=a[l1][r1];	
		return;
	}
	
	int m1=(l1+l2)/2,m2=(r1+r2)/2;
	build(l1,r1,m1,m2,p*4);
	if(m2+1<=r2) build(l1,m2+1,m1,r2,p*4+1);
	if(m1+1<=l2) build(m1+1,r1,l2,m2,p*4+2);
	if(m1+1<=l2&&m2+1<=r2) build(m1+1,m2+1,l2,r2,p*4+3);
	
	t[p].val=t[p*4].val+t[p*4+1].val+t[p*4+2].val+t[p*4+3].val;
	
}

void change(int l1,int r1,int l2,int r2,int d,int p)
{
	if(t[p].l1>=l1&&t[p].r1>=r1&&t[p].l2<=l2&&t[p].r2<=r2)
	{
		t[p].val+=(t[p].l2-t[p].l1+1)*(t[p].r2-t[p].r1+1)*d;
		t[p].add+=d;
		return;
	}
	
	int m1=(t[p].l1+t[p].l2)/2,m2=(t[p].r1+t[p].r2)/2;
	
	if(l1<=m1&&r1<=m2) change(l1,r1,l2,r2,d,p*4);
	if(l1<=m1&&r2>m2) change(l1,r1,l2,r2,d,p*4+1);
	if(l2>m1&&r1<=m2) change(l1,r1,l2,r2,d,p*4+2);
	if(l2>m1&&r2>m2) change(l1,r1,l2,r2,d,p*4+3);
	
	t[p].val=t[p*4].val+t[p*4+1].val+t[p*4+2].val+t[p*4+3].val+(t[p].l2-t[p].l1+1)*(t[p].r2-t[p].r1+1)*t[p].add;
}

int ask(int l1,int r1,int l2,int r2,int d,int p)
{
	if(t[p].l1>=l1&&t[p].r1>=r1&&t[p].l2<=l2&&t[p].r2<=r2) return t[p].val+(t[p].l2-t[p].l1+1)*(t[p].r2-t[p].r1+1)*d;
	int m1=(t[p].l1+t[p].l2)/2,m2=(t[p].r1+t[p].r2)/2,res=0;
	if(l1<=m1&&r1<=m2) res+=ask(l1,r1,l2,r2,d+t[p].add,p*4);
	if(l1<=m1&&r2>m2) res+=ask(l1,r1,l2,r2,d+t[p].add,p*4+1);
	if(l2>m1&&r1<=m2) res+=ask(l1,r1,l2,r2,d+t[p].add,p*4+2);
	if(l2>m1&&r2>m2) res+=ask(l1,r1,l2,r2,d+t[p].add,p*4+3);
	return res;
}
int main()
{
	for(int i=1;i<=4;++i)
	for(int j=1;j<=4;++j)
	a[i][j]=1;
	build(1,1,4,4,1);
	
	change(1,1,3,3,1,1);
	
	for(int i=1;i<=4;++i)
	{
		for(int j=1;j<=4;++j)
		printf("%d ",ask(1,1,i,j,0,1));
		printf("\n");
	}
}

5.KD_tree

即多维线段树。

由于有些问题需要更高的维度，并且矩形分法浪费空间非常大，且难打还容易写错，故引出KD_tree结构。

即k个维度轮流作为二分的依据进行分割。

比如二维，先分x轴再分y轴再分x轴。

由于每个节点实际上的维度值有k个，下一个节点考虑的第x值在这个节点是没有考虑的，为了保证维度数值的下传不出错，应给给每个节点额外开一个数组记录此时的所有维度值。

但由于我们实际考虑的只有一个，其他都是为了下传不出错，故可以直接开一个全局变量，每次下传时把此节点分割后的值赋入全局变量，回溯一次后修改成另一子节点对应的第k维的值。

为了保证回溯后再到另一节点时，其他维度的值和进入第一个节点时一样，每次建立节点之后应有一个复原操作。

#include<bits/stdc++.h>
using namespace std;

const int N=100010,wd=2;
int n,m,l[wd],r[wd];//有俩维度
bool bz[wd];
struct t_
{
	int l,r,k,val,add,inc;
}t[10000005];//谁知道是什么玄学内存

void build(int k,int check,int p)
{
	t[p].l=l[k];
	t[p].r=r[k];
	t[p].k=k;
	if(l[k]==r[k]) check++;
	if(check==wd)
	{
		t[p].inc=1;
		t[p].val=1;
		return;
	}
	
	k=(k+1)%wd;
	while(l[k]==r[k]) k=(k+1)%wd;
	
	int m=(l[k]+r[k])/2,ll=l[k],rr=r[k];
	
	r[k]=m;
	build(k,check,p*2);
	
	l[k]=m+1,r[k]=rr;
	build(k,check,p*2|1);
	
	l[k]=ll,r[k]=rr;
	
	t[p].val=t[p*2].val+t[p*2|1].val;
	t[p].inc=t[p*2].inc+t[p*2|1].inc;
}

void change(int check,int d,int p)
{
	int ff=0;
	if(!bz[t[p].k]&&t[p].l>=l[t[p].k]&&t[p].r<=r[t[p].k]) ff=1,bz[t[p].k]=1,check++;
	
	if(check==wd)
	{
		if(ff) bz[t[p].k]=0;
		t[p].val+=d*t[p].inc,t[p].add+=d;
		return;
	}
	int m=t[p*2].r,k=t[p*2].k;
	
	if(l[k]<=m) change(check,d,p*2);
	if(r[k]>m) change(check,d,p*2|1);
	
	if(ff) bz[t[p].k]=0;
	t[p].val=t[p*2].val+t[p*2|1].val+t[p].add*t[p].inc;
}

int ask(int check,int d,int p)
{	
	int ff=0;
	if(!bz[t[p].k]&&t[p].l>=l[t[p].k]&&t[p].r<=r[t[p].k]) ff=1,bz[t[p].k]=1,check++;
	
	if(check==wd)
	{
		if(ff) bz[t[p].k]=0;
		return t[p].val+d*t[p].inc;
	}
	int m=t[p*2].r,k=t[p*2].k,res=0;
	
	if(l[k]<=m) res+=ask(check,d+t[p].add,p*2);
	if(r[k]>m) res+=ask(check,d+t[p].add,p*2|1);
	
	if(ff) bz[t[p].k]=0;
	return res;
}


int main()
{
	l[0]=l[1]=1;
	r[0]=r[1]=1000;
	build(0,0,1);
	
	l[0]=l[1]=1;
	r[0]=r[1]=99;
	change(0,1,1);
	
	l[0]=l[1]=1;
	
	
	for(int i=1;i<=1000;++i)
	{
		for(int j=1;j<=1000;++j)
		{
			r[0]=i,r[1]=j;
			bz[0]=bz[1]=0;
			ask(0,0,1);
		}
//		printf("\n");
	}
	
	printf("Run time is %lfs",(double)clock()/CLOCKS_PER_SEC);
}

由于很多时候，我们的维度没有必要全部开完，比如以下例题：

陌上花开

输入 #1

输出 #1

首先按a排序转换为二维计算。由于有些b区间之下可能根本不存在某段c区间，即矩形有些部分不存在，开出来反而浪费空间。

所以KD_tree经常采用动态开点。

70（代码意外地简短）

#include<bits/stdc++.h>
using namespace std;

const int N=1e6+5,wd=2;
int n,m,tt=1,cnt[N],r[2];
bool bz[2];
struct e_
{
	int a,b,c;
	friend bool operator<(e_ a,e_ b)
	{
		return a.a<b.a;
	}
}e[N];
struct t_
{
	int l[2],r[2],ls,rs,k,val;
}t[N];

int build(int op,int m,int k,int p)
{
	//非二分维度不变 
	t[++tt].l[k^1]=t[p].l[k^1];
	t[tt].r[k^1]=t[p].r[k^1];
	//如果是左子树
	if(op) t[tt].l[k]=t[p].l[k],t[tt].r[k]=m;
	else t[tt].l[k]=m+1,t[tt].r[k]=t[p].r[k];
	
	t[tt].k=k;
	
	return tt; 
}
void change(int p)
{
	if(t[p].l[0]==t[p].r[0]&&t[p].l[1]==t[p].r[1])
	{
		t[p].val++;
		return;
	}
	
	int k=t[p].k^1,m=(t[p].l[k]+t[p].r[k])/2;
	
	if(r[k]<=m)
	{
		if(!t[p].ls) t[p].ls=build(1,m,k,p);
		change(t[p].ls);
	}
	else
	{
		if(!t[p].rs) t[p].rs=build(0,m,k,p);
		change(t[p].rs);
	}
	
	t[p].val=t[t[p].ls].val+t[t[p].rs].val;
}

int ask(int p)
{
	if(t[p].r[0]<=r[0]&&t[p].r[1]<=r[1]) return t[p].val;
	
	int k=t[p].k^1,m=(t[p].l[k]+t[p].r[k])/2,res=0;
	
	res+=ask(t[p].ls);
	if(r[k]>m) res+=ask(t[p].rs);
	
	return res;
}

int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;++i) 
	scanf("%d %d %d",&e[i].a,&e[i].b,&e[i].c),
	t[1].r[0]=max(t[1].r[0],e[i].b),
	t[1].r[1]=max(t[1].r[1],e[i].c);
	
	t[1].l[0]=t[1].l[1]=1;
	
	sort(e+1,e+n+1);
	
	for(int i=1;i<=n;)
	{ 
		int j=i,val=e[i].a;
		while(e[i].a==val)
		{
			r[0]=e[i].b;
			r[1]=e[i].c;
			
			change(1);
			i++;
		}
		while(j<i)
		{
			r[0]=e[j].b;
			r[1]=e[j].c;
			cnt[ask(1)-1]++;
			j++;
		} 
	}
	for(int i=0;i<n;++i) printf("%d\n",cnt[i]);
	
}

6.线段树合并与分裂

手模一下可以很快理解。

基础

void Update(int p)
{
	因题制宜
}
int New()
{
	return rab[0]?rab[rab[0]--]:++tot;
}
void Throw(int &p)
{
	rab[++rab[0]]=p;
	lc[p]=rc[p]=0;
	数据更新
	p=0;
}
/*一般涉及合并分裂的题都涉及动态开点*/
void Change(int l,int r,int x,int &p)
{
	if(!p) p=New();
	if(l==r){更新;return;}
	
	int mid=(l+r)>>1;
	if(x<=mid) Change(l,mid,x,lc[p]);
	else Change(mid+1,r,x,rc[p]);
	
	Update(p);
	return;
}

合并

int Merge(int l,int r,int u,int v)
{
	if(!u||!v) return u|v;
	int p=New();
	if(l==r)
	{
		更新;
	}
	else
	{
		int mid=(l+r)>>1;
		lc[p]=Merge(l,mid,lc[u],lc[v]);
		rc[p]=Merge(mid+1,r,rc[u],rc[v]);
		Update(p);
	}
	Throw(u);Throw(v);
	return p;
}

单点分裂

void Split(int l,int r,int x,int &p1,int &p2)
{
	if(l==r)
	{
		p2=p1;p1=0;
		return;
	}
    p2=New();
    
    int mid=(l+r)>>1;
    if(x<=mid) Split(l,mid,x,lc[p1],lc[p2]);
    else Split(mid+1,r,x,rc[p1],rc[p2]);
    
    Update(p2);
	if(!lc[p1]&&!rc[p1]) Throw(p1);
	else Update(p1);
	return;
}

区间分裂

void Split(int l,int r,int x,int y,int &p1,int &p2)
{
	if(x>=l&&y<=r)
	{
		p2=p1;p1=0;
		return;
	}
	p2=New();
	int mid=(l+r)>>1;
	if(x<=mid) Split(l,mid,x,y,lc[p1],lc[p2]);
	if(y>mid) Split(mid+1,r,x,y,rc[p1],rc[p2]);
	
	if(!lc[p1]&&!rc[p1]) Throw(p1);
	else Update(p1);
	
	return;
}

P4556 线段树合并模板题

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5,Z=1e5,M=4e6+5,INF=1e9+5;
int n,m,ans[N];
int te,v[N<<1],pre[N<<1],tail[N];
int fa[N],top[N],dep[N],siz[N],son[N];
int ta,av[N<<2],aw[N<<2],ap[N<<2],at[N<<2];
int tot,lc[M],rc[M],root[N];
int val[M],id[M],rab[M];

inline void add(int x,int y)
{
	++te;v[te]=y;pre[te]=tail[x];tail[x]=te;
}

inline void Dfs1(int x)
{
	siz[x]=1;
	for(int i=tail[x];i;i=pre[i])
	if(v[i]!=fa[x]) 
	{
		fa[v[i]]=x;
		dep[v[i]]=dep[x]+1;
		Dfs1(v[i]);
		
		siz[x]+=siz[v[i]];
		if(siz[v[i]]>siz[son[x]]) son[x]=v[i];
	}
}

inline void Dfs2(int x,int y)
{
	top[x]=y;
	if(!son[x]) return;
	Dfs2(son[x],y);
	for(int i=tail[x];i;i=pre[i])
	if(v[i]!=fa[x]&&v[i]!=son[x]) Dfs2(v[i],v[i]);
}

inline int Lca(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		x=fa[top[x]];
	}
	return dep[x]<dep[y]?x:y;
}

inline void Insert(int x,int y,int z)
{
	if(!x) return;
	++ta;av[ta]=y;aw[ta]=z;ap[ta]=at[x];at[x]=ta;
}
inline int New()
{
	return rab[0]?rab[rab[0]--]:++tot;
}
inline void Update(int p)
{
	if(val[lc[p]]>=val[rc[p]]) val[p]=val[lc[p]],id[p]=id[lc[p]];
	else val[p]=val[rc[p]],id[p]=id[rc[p]];
}

inline void Change(int l,int r,int x,int y,int &p)
{
	if(!p) p=New();
	if(l==r){val[p]+=y;id[p]=l;return;}
	
	int mid=(l+r)>>1;
	if(x<=mid) Change(l,mid,x,y,lc[p]);
	else Change(mid+1,r,x,y,rc[p]);
	
	Update(p);
	if(!val[p]) id[p]=0;
}
inline void Throw(int p)
{
	rab[++rab[0]]=p;
	lc[p]=rc[p]=val[p]=id[p]=0;
}

inline int Merge(int l,int r,int u,int v)
{
	if(!u||!v) return u|v;
	int p=New(),mid=(l+r)>>1;
	
	if(l==r)
	{
		val[p]=val[u]+val[v];
		id[p]=l;
	}
	else
	{
		lc[p]=Merge(l,mid,lc[u],lc[v]);
		rc[p]=Merge(mid+1,r,rc[u],rc[v]);
		Update(p);
	}
	Throw(u);Throw(v);
	return p;
}

inline void Dfs3(int x)
{
	for(int i=tail[x];i;i=pre[i])
	if(v[i]!=fa[x]) Dfs3(v[i]);
	
	for(int i=at[x];i;i=ap[i])
	Change(1,Z,av[i],aw[i],root[x]);
	
	ans[x]=id[root[x]];
	
	if(fa[x]) root[fa[x]]=Merge(1,Z,root[fa[x]],root[x]);
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1,x,y;i<n;++i) scanf("%d %d",&x,&y),add(x,y),add(y,x);
	Dfs1(1);Dfs2(1,1);
	for(int i=1,u,v,tp;i<=m;++i)
	{
		scanf("%d %d %d",&u,&v,&tp);
		int lca=Lca(u,v);
		Insert(u,tp,1);
		Insert(v,tp,1);
		Insert(lca,tp,-1);
		Insert(fa[lca],tp,-1);
	}
	Dfs3(1);
	for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
}

7.TIPS

线段树build有两种写法。

一对一赋值。

void build(int l,int r,int p)
{
	t[p].l=l;
	t[p].r=r;
	if(l==r)
	{
		t[p].val=a[l];
		t[p].flag=(t[p].val<=1);
		return;
	}
	
	int m=(l+r)/2;
	
	build(l,m,p*2);
	build(m+1,r,p*2+1);
	
	t[p].val=t[p*2].val+t[p*2+1].val;
	t[p].flag=(t[p].val<=1);
}

整体赋值

void build(int l,int r,int p)
{
	if(l==r)
	{
		t[p]=(t_){l,r,0,a[l]};
		t[p].flag=(t[p].val<=1);
		return;
	}
	
	int m=(l+r)/2;
	
	build(l,m,p*2);
	build(m+1,r,p*2+1);
	
	t[p]=(t_){l,r,0,t[p*2].val+t[p*2+1].val};
	t[p].flag=(t[p].val<=1);
}

当测试数据为一组含有1005（1e3）个数的随机数据时，一对一赋值耗时0.002s，整体赋值耗时0.001s。

当测试数据为一组含有10005（1e4）个数的随机数据时，一对一赋值耗时0.005s，整体赋值耗时0.009s。

当测试数据为一组含有100005（1e5）个数的随机数据时，一对一赋值耗时0.035s，整体赋值耗时0.036s。

当测试数据为一组含有100005（1e6）个数的随机数据时，一对一赋值耗时0.33s，整体赋值耗时0.34s~0.36s。

posted @ 2020-10-23 18:56 林生。阅读(106) 评论(0) 收藏举报

刷新页面返回顶部

小祈の博客

——为了爱与你理想中的远方

线段树

线段树

1.单点修改

【JSOI 2008】最大数

你能回答这些问题吗

区间最大公约数

2.区间修改

1.转化为单点修改。

2.延迟标记

一个简单的整数问题2

【BZOJ 3211】花神游历各国

【AHOI】维护序列

3.标记永久化

3.扫描线

亚特兰蒂斯

窗内的星星

圆的扫描线

4.二维线段树（矩形四分）

5.KD_tree

陌上花开

6.线段树合并与分裂

基础

合并

单点分裂

区间分裂

P4556 线段树合并模板题

7.TIPS

公告