树状数组
树状数组
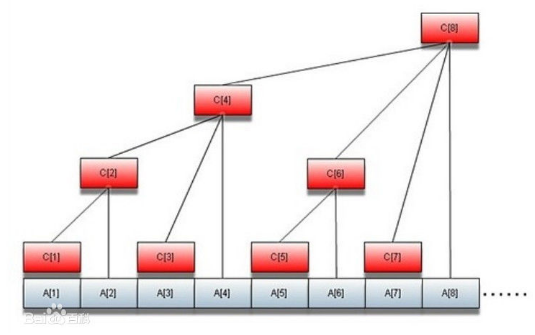
树状数组即利用二进制进行储存,若x的最低位1在第i位,则x储存x-2i~x的数值,可利用二进制进行快速修改与查询。
树状数组便于快速查询前缀和,查询和修改的复杂度皆为\(O(log~2~N)\),而普通前缀和查询的复杂度为\(O(1)\),但修改的复杂度为\(O(N)\),效率太低。
一维树状数组
修改函数
void add(int x,int y)
{
for(;x<=n;x+=x&-x) c[x]+=y;
}
查询函数
int ask(int x)
{
int res=0;
for(;x;x-=x&-x) res+=c[x];
return res;
}
【CQOI 2006】简单题时间限制
【题目描述】
有一个 n 个元素的数组,每个元素初始均为 0。有 m 条指令,要么让其中一段连续序列数字反转——0 变 1,1 变 0(操作 1),要么询问某个元素的值(操作 2)。
【数据输入】
第一行包含两个整数 n,m,表示数组的长度和指令的条数;
以下 m 行,每行的第一个数 t 表示操作的种类:
若 t=1,则接下来有两个数 L,R,表示区间 [L,R] 的每个数均反转;
若 t=2,则接下来只有一个数 i,表示询问的下标。
【数据输出】
每个操作 2 输出一行(非 0 即 1),表示每次操作 2 的回答。
【输入样例】
20 10
1 1 10
2 6
2 12
1 5 12
2 6
2 15
1 6 16
1 11 17
2 12
2 6
【输出样例】
1
0
0
0
1
1
【数据范围】
数据范围与提示:
对于 50% 的数据,1≤n≤103,1≤m≤104 ;
对于 100% 的数据,1≤n≤105,1≤m≤5×105 ,保证 L≤R。
#include<bits/stdc++.h>
using namespace std;
#define N 500005
int n,m,c[N];
void add(int x)
{
for(;x<=n;x+=x&-x)
c[x]^=1;
}
int ask(int x)
{
int res=0;
for(;x;x-=x&-x)
res^=c[x];
return res;
}
int main()
{
scanf("%d %d",&n,&m);
while(m--)
{
int op,a,b;
scanf("%d %d",&op,&a);
if(op==1)
{
scanf("%d",&b);
add(a);
add(b+1);
}
else
printf("%d\n",ask(a));
}
}
逆序对
【问题描述】
设A[1..n]是一个包含n个不同数的数组。如果在i<j的情况下,有A[i]>A[j],则(i, j)就称为A中的一个逆序对。比如<2,3,8,6,1>有5个逆序对:(2,1)(3,1)(8,6)(8,1)(6,1). 现在给出一个包含不同元素的数组,请你求出这个数组中逆序对的个数。 【输入格式】
第一行为数组的数据个数n(n=3000000),第二行开始的n个数组元素,相邻元素之间用一个空格隔开。
【输出格式】
输出为一行,测试数据中的逆序对的个数。
【样例输入】
5
2 3 8 6 1
【样例输出】
5
【数据范围】
数组中的每一个数的绝对值均小于等于100。
树状数组存储a[i]的值,查询小于等于a[i]的值,i-a[i]即为比a[i]大的值的数量。
#include<bits/stdc++.h>
using namespace std;
#define N 3000010
#define p 105
int n,a[N],s[N];
long long ans,c[p*2];
void add(int x,long long y)
{
for(;x<=p*2;x+=x&-x)
c[x]+=y;
}
long long ask(int x)
{
long long res=0;
for(;x;x-=x&-x) res+=c[x];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i)
{
add(a[i]+p,1);
ans+=i-ask(a[i]+p);
}
printf("%lld",ans);
}
楼兰图腾
在完成了分配任务之后,西部314来到了楼兰古城的西部。
相传很久以前这片土地上(比楼兰古城还早)生活着两个部落,
一个部落崇拜尖刀(‘V’),一个部落崇拜铁锹(‘∧’),
他们分别用V和∧的形状来代表各自部落的图腾。
西部314在楼兰古城的下面发现了一幅巨大的壁画,壁画上
被标记出了N个点,经测量发现这N个点的水平位置和竖直
位置是两两不同的。
西部314认为这幅壁画所包含的信息与这N个点的相对位置
有关,因此不妨设坐标分别为(1,y1),(2,y2),…,(n,yn),
其中y1~yn是1到n的一个排列。
西部314打算研究这幅壁画中包含着多少个图腾。
如果三个点(i,yi),(j,yj),(k,yk)满足1≤i<j<k≤n
且yi>yj,yj<yk,则称这三个点构成V图腾;
如果三个点(i,yi),(j,yj),(k,yk)满足1≤i<j<k≤n
且yi<yj,yj>yk,则称这三个点构成∧图腾;
西部314想知道,这n个点中两个部落图腾的数目。
因此,你需要编写一个程序来求出V的个数和∧的个数。
输入格式
第一行一个数n。
第二行是n个数,分别代表y1,y2,…,yn。
输出格式
两个数,中间用空格隔开,依次为V的个数和∧的个数。
数据范围
对于所有数据,n≤200000,且输出答案不会超过int64。
y1~yn 是 1 到 n 的一个排列。
输入样例:
5
1 5 3 2 4
输出样例:
3 4
#include<bits/stdc++.h>
using namespace std;
#define maxn 200005
int n,m;
int a[maxn],c[maxn];
void init()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
c[i]=a[i];
}
}
void lsh()
{
map<int,int>rep;
sort(c+1,c+n+1);
m=unique(c+1,c+n+1)-c-1;
for(int i=1;i<=m;i++)
rep[c[i]]=i;
for(int i=1;i<=n;i++)
a[i]=rep[a[i]];
}
long long ask(int x)
{
int ans=0;
for(;x;x-=x&-x) ans+=c[x];
return ans;
}
void add(int x,int y)
{
for(;x<=m;x+=x&-x)
c[x]+=y;
}
long long numV()
{
long long ans=0;
long long know[maxn];
memset(c,0,sizeof(c));
for(int i=1;i<=n;i++)
{
know[i]=ask(m-a[i]);
add(m-a[i]+1,1);
}
memset(c,0,sizeof(c));
for(int i=n;i;i--)
{
ans+=know[i]*ask(m-a[i]);
add(m-a[i]+1,1);
}
return ans;
}
long long numv()
{
long long ans=0;
long long know[maxn];
memset(c,0,sizeof(c));
for(int i=1;i<=n;i++)
{
know[i]=ask(a[i]-1);
add(a[i],1);
}
memset(c,0,sizeof(c));
for(int i=n;i;i--)
{
ans+=know[i]*ask(a[i]-1);
add(a[i],1);
}
return ans;
}
int main()
{
init();
lsh();
printf("%lld %lld",numV(),numv());
}
区间修改,单点查询
给定长度为N的数列A,然后输入M行操作指令。
第一类指令形如“C l r d”,表示把数列中第l~r个数都加d。
第二类指令形如“Q X”,表示询问数列中第x个数的值。
对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数N和M。
第二行包含N个整数A[i]。
接下来M行表示M条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤105,
|d|≤10000,
|A[i]|≤1000000000
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例:
4
1
2
5
树状数组维护增加或者减少的值
#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
int n,m;
long long num[105],b[maxn];
long long ask(int x)
{
long long ans=0;
for(;x;x-=x&-x) ans+=b[x];
return ans;
}
void add(int x,long long y)
{
for(;x<=n;x+=x&-x) b[x]+=y;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld",&num[i]);
while(m--)
{
char op[2];
int l;
scanf("%s %d",&op,&l);
if(op[0]=='Q') printf("%lld\n",num[l]+ask(l));
else
{
int r;
long long d;
scanf("%d %lld",&r,&d);
add(l,d);
add(r+1,-d);
}
}
return 0;
}
区间修改,区间查询
给定一个长度为N的数列A,以及M条指令,每条指令可能是以下两种之一:
1、“C l r d”,表示把 A[l],A[l+1],…,A[r] 都加上 d。
2、“Q l r”,表示询问 数列中第 l~r 个数的和。
对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数N,M。
第二行N个整数A[i]。
接下来M行表示M条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤105,
|d|≤10000,
|A[i]|≤1000000000
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例:
4
55
9
15
首先我们可以开一个数组B,然后对于每条C操作,我们直接利用前缀和的思想.
把b[l]+=d;
把b[r+1]-=d;
然后我们就成功达成成就,把维护序列的具体值,转化为维护指令的累计影响,每次操作的影响,在l处开始,然后在r+1处消除.然后就让单点修改可以维护区间修改.
现在b数组的前缀和就是∑xi=1b[i]∑i=1xb[i] 就是经过指令后a[x]增加的值,那么序列a的前缀和a[1~x]增加的值就是:
然后上式就可以转换为
然后通过上面这个式子,我们就把原来的数组,经过差分操作去维护两个树状数组,一个维护di,一个维护di×i这样的话,我们在区间修改的过程中,就可以在两个树状数组中去查询得到前缀和,然后同理,区间修改操作就是差分数组的修改,每次只需要修改两个点,完美的将区间再次转换为单调修改。
#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
int n,m;
long long a[maxn];
long long b[2][maxn];
inline int low_bit(int x)
{
return x&-x;
}
long long ask(int k,int x)
{
long long ans=0;
for(;x;x-=low_bit(x)) ans+=b[k][x];
return ans;
}
void add(int k,int x,int y)
{
for(;x<=n;x+=low_bit(x)) b[k][x]+=y;
}
int main()
{
char dd;
int l,r,d;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
a[i]+=a[i-1];
}
for(int i=1;i<=m;i++)
{
cin>>dd;
if(dd=='Q')
{
scanf("%d %d",&l,&r);
printf("%lld\n",a[r]+(r+1)*ask(0,r)-ask(1,r)-a[l-1]-l*ask(0,l-1)+ask(1,l-1));
}
else
{
scanf("%d %d %d",&l,&r,&d);
add(0,l,d);
add(0,r+1,-d);
add(1,l,l*d);
add(1,r+1,-(r+1)*d);
}
}
}
谜一样的牛(树状数组+二分查找)
有n头奶牛,已知它们的身高为 1~n 且各不相同,但不知道每头奶牛的具体身高。
现在这n头奶牛站成一列,已知第i头牛前面有Ai头牛比它低,求每头奶牛的身高。
输入格式
第1行:输入整数n。
第2..n行:每行输入一个整数Ai,第i行表示第i头牛前面有Ai头牛比它低。
(注意:因为第1头牛前面没有牛,所以并没有将它列出)
输出格式
输出包含n行,每行输出一个整数表示牛的身高。
第i行输出第i头牛的身高。
数据范围
1≤n≤105
输入样例:
5
1
2
1
0
输出样例:
2
4
5
3
1
等价于倒序找剩余的数中第k大的数。
满足条件的数可能有很多个,找最小的一个,利用bz数组表示该格子是否可取。
c数组初始化时每个位置都为1,循环查找时找到一个位置就把这个位置踢出队列,对应的c数组的位置变为0,即减去1
#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
int n;
int low[maxn],b[maxn],ans[maxn];
bool bz[maxn];
int ask(int x)
{
int ans=0;
for(;x;x-=x&-x) ans+=b[x];
return ans;
}
void add(int x,int y)
{
for(;x<=n;x+=x&-x) b[x]+=y;
}
int main()
{
scanf("%d",&n);
for(int i=2;i<=n;i++) scanf("%d",&low[i]);
for(int i=1;i<=n;i++)
{
bz[i]=1;
add(i,1);
}
//In reverse order,
//1.the height of the first cow will not affect 1-i-1,
//2.the height of the first cow is the C [i] of the remaining number
for(int i=n;i;i--)
{
int l=1,r=n+1,m,k=low[i]+1;
while(l<r)
{
m=(l+r)/2;
if(ask(m)<k) l=m+1;
else r=m;
}
while(!bz[l]) l++;
bz[l]=0;
add(l,-1);
ans[i]=l;
}
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
}
买票(树状数组+二分查找)
题目描述
【题目描述】
达达在买回家的火车票,因为正值春运,售票处排起了长队。
因为晚上室内光线很暗,所以很多人趁机插队。
现在给每个人赋予一个整数作为编号,告诉你每一个排队的人的编号,和他进入队列时的具体位置。
请你确定最终的队列顺序。
【输入格式】
输入可能包含多组测试用例。
对于每组测试用例,第一行包含整数N,表示排队的总人数。
接下来N行,每行两个整数Pi,Vi,第i行数据表示第i个人进入队列时的位置以及他的个人编号。
一个人的Pi值具体表示为当该人员进入队列时,他前面的人数。
例如,如果一个人插到了队首,则其Pi值为0,如果插到了第三个位置(第二个人后面),则其Pi值为2。
【输出格式】
每个测试用例,输出一行包含N个整数(表示每个人的编号)的结果,表示最终的人员队列顺序。
每个结果占一行,同行数据之间空格隔开。
【数据范围】
1≤N≤200000,
0≤Vi≤32767,
0≤Pi≤i−1
【输入样例】
4
0 77
1 51
1 33
2 69
4
0 20523
1 19243
1 3890
0 31492
【输出样例】
77 33 69 51
31492 20523 3890 19243
做法同谜一样的牛。
#include<bits/stdc++.h>
using namespace std;
#define N 200010
int n,q[N],a[N],c[N],ans[N];
bool bz[N];
void add(int x,int y)
{
for(;x<=n;x+=x&-x) c[x]+=y;
}
int ask(int x)
{
int res=0;
for(;x;x-=x&-x) res+=c[x];
return res;
}
int main()
{
while(~scanf("%d",&n))
{
for(int i=1;i<=n;i++)
{
bz[i]=1;
add(i,1);
}
for(int i=1;i<=n;++i)
scanf("%d %d",&q[i],&a[i]);
for(int i=n;i;--i)
{
int k=q[i]+1,l=1,r=n+1,m;
while(l<r)
{
m=(l+r)/2;
if(ask(m)<k) l=m+1;
else r=m;
}
while(!bz[l]) l++;
add(l,-1);
bz[l]=0;
ans[l]=a[i];
}
for(int i=1;i<=n;++i) printf("%d ",ans[i]);
printf("\n");
}
}
二维树状数组
在横行上进行树状储存,竖行上也进行树状储存。
每次询问返回\(∑1<=i<=n∑1<=j<=mA[i][j]\)
横行竖行必须分开循环。
修改
void add(int x,int y,long long val)
{
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=m;j+=j&-j)
c[i][j]+=val;
}
询问
long long ask(int x,int y)
{
long long res=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
res+=c[i][j];
return res;
}
二维树状数组模板
#include<bits/stdc++.h>
using namespace std;
#define N 5005
int n=5,m=5,r;
long long c[N][N];
void add(int x,int y,long long val)
{
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=m;j+=j&-j)
c[i][j]+=val;
}
long long ask(int x,int y)
{
long long res=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
res+=c[i][j];
return res;
}
int main()
{
cout<<"数组A为:\n";
for(int i=1;i<=5;++i)
{
for(int j=1;j<=5;++j)
{
add(i,j,1);
cout<<1<<' ';
}
cout<<"\n";
}
cout<<"\n\n";
cout<<"数组C为:\n";
for(int i=1;i<=5;++i)
{
for(int j=1;j<=5;++j)
{
cout<<c[i][j]<<' ';
}
cout<<"\n";
}
cout<<"\n\n";
cout<<"数组A求和为:\n" ;
for(int i=1;i<=5;++i)
{
for(int j=1;j<=5;++j)
{
long long val=ask(i,j);
cout<<val<<' ';
}
cout<<"\n";
}
}
输出为
数组A为:
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
数组C为:
1 2 1 4 1
2 4 2 8 2
1 2 1 4 1
4 8 4 16 4
1 2 1 4 1
数组A求和为:
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
5 10 15 20 25
二维单点增加、区间查询
题目描述
【题目描述】
对于数组d[1..n, 1..m], 初始值全为0,我们有两个操作0和1。对于0 a b c操作,表示把d[a,b]增加c;对于1 a1 b1 a2 b2操作,表示询问满足a1<=i<=a2,b1<=j<=b2的d[i,j]的和。
【数据输入】
第一行三个数n,m,r(1<=n,m<=5000,1<=r<=100000),n,m如题,r表示操作个数。接下来r行描述操作。对于0操作1<=a<=n,1<=b<=m,1<=c<=1000;对于1操作,1<=a1<=a2<=n,1<=b1<=b2<=m。所有数均为整数。
【数据输出】
对于每个1操作,输出一行一个整数,为所求答案。
【输入样例】
2 2 2
0 1 1 123
1 1 1 2 2
【输出样例】
123
容斥原理。
ans=ask(a2,b2);
ans-=ask(a1-1,b2);
ans-=ask(a2,b1-1);
ans+=ask(a1-1,b1-1);
#include<bits/stdc++.h>
using namespace std;
#define N 5001
int n,m,r,c[N][N];
void add(int x,int y,int val)
{
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=m;j+=j&-j)
c[i][j]+=val;
}
int ask(int x,int y)
{
int res=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
res+=c[i][j];
return res;
}
int main()
{
scanf("%d %d %d",&n,&m,&r);
while(r--)
{
int op;
scanf("%d",&op);
if(!op)
{
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
add(a,b,c);
}
else
{
int a1,b1,a2,b2;
int ans;
scanf("%d %d %d %d",&a1,&b1,&a2,&b2);
ans=ask(a2,b2);
ans-=ask(a1-1,b2);
ans-=ask(a2,b1-1);
ans+=ask(a1-1,b1-1);
printf("%d\n",ans);
}
}
}
二维区间增加、单点查询
【题目描述】
对于数组d[1..n,1..m],初始值全为0,我们有两个操作0和1。对于0 a1 b1 a2 b2 c操作,表示把满足a1<=i<=a2,b1<=j<=b2的d[i,j]增加c;对于1 a b操作,表示询问d[a,b]的值。
【数据输入】
第一行三个数n,m,r(1<=n,m<=5000,1<=r<=100000),n,m如题,r表示操作个数。接下来r行描述操作。对于0操作1<=a1<=a2<=n,1<=b1<=b2<=m,1<=c<=1000;对于1操作,1<=a<=b<=n。所有数均为整数。
【数据输出】
对于每个1操作,输出一行一个整数,为所求答案。
【输入样例】
3 3 2
0 1 1 2 2 3
1 1 2
【输出样例】
3
容斥原理。
add(a1,b1,c);
add(a2+1,b1,-c);
add(a1,b2+1,-c);
add(a2+1,b2+1,c);
#include<bits/stdc++.h>
using namespace std;
#define N 5050
int n,m,r,c[N][N];
void add(int x,int y,int val)
{
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=m;j+=j&-j)
c[i][j]+=val;
}
int ask(int x,int y)
{
int res=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
res+=c[i][j];
return res;
}
int main()
{
scanf("%d %d %d",&n,&m,&r);
while(r--)
{
int op;
scanf("%d",&op);
if(!op)
{
int a1,b1,a2,b2,c;
scanf("%d %d %d %d %d",&a1,&b1,&a2,&b2,&c);
add(a1,b1,c);
add(a2+1,b1,-c);
add(a1,b2+1,-c);
add(a2+1,b2+1,c);
}
else
{
int a,b;
scanf("%d %d",&a,&b);
printf("%d\n",ask(a,b));
}
}
}
二维区间增加、区间查询
【题目描述】
对于数组d[1..n,1..m],初始值全为0,我们有两个操作0和1。对于0 a1 b1() a2 b2 c操作,表示把满足a1<=i<=a2,b1<=j<=b2的d增加c;对于1 a1 b1 a2 b2操作,表示询问满足a1<=i<=a2,b1<=j<=b2的d的和。
【数据输入】
第一行三个数n,m,r(1<=n,m<=5000,1<=r<=100000),n,m如题,r表示操作个数。接下来r行描述操作。对于0操作1<=a1<=a2<=n,1<=b1<=b2<=m,1<=c<=10000;对于1操作,1<=a1<=a2<=n,1<=b1<=b2<=m。所有数均为整数。保证运算过程中所有数不超过2^63-1。
【数据输出】
对于每个1操作,输出一行一个整数,为所求答案。
【输入样例】
3 3 2
0 1 1 2 2 1
1 2 2 3 3
【输出样例】
1
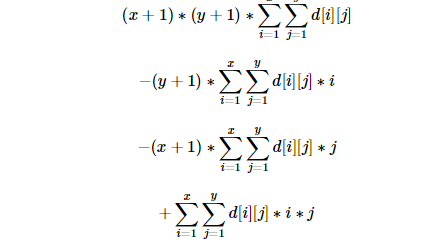
#include<bits/stdc++.h>
using namespace std;
#define N 5005
#define ll long long
int n,m,k;
ll c[4][N][N];
void add(int x,int y,ll val)
{
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=m;j+=j&-j)
{
c[0][i][j]+=val;
c[1][i][j]+=(ll)y*val;
c[2][i][j]+=(ll)x*val;
c[3][i][j]+=(ll)x*y*val;
}
}
ll ask(int k,int x,int y)
{
ll res=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
res+=c[k][i][j];
return res;
}
ll get(int x,int y)
{
return (ll)(x+1)*(y+1)*ask(0,x,y)-(ll)(x+1)*ask(1,x,y)-(ll)(y+1)*ask(2,x,y)+ask(3,x,y);
}
int main()
{
scanf("%d %d %d",&n,&m,&k);
int op,a1,a2,b1,b2;
ll c;
while(k--)
{
scanf("%d %d %d %d %d",&op,&a1,&b1,&a2,&b2);
if(!op)
{
scanf("%lld",&c);
add(a1,b1,c);
add(a1,b2+1,-c);
add(a2+1,b1,-c);
add(a2+1,b2+1,c);
}
else printf("%lld\n",get(a2,b2)-get(a1-1,b2)-get(a2,b1-1)+get(a1-1,b1-1));
}
}
先全部修改再计算
手动容斥!!!!
在200*200的坐标系里给定n个矩形,可以最多再添加两个互不重叠的矩形(题目中没有给出,由编者自己添加),求被m个矩形覆盖的面积有多大。
#include<bits/stdc++.h>
using namespace std;
const int N=205;
int n,m,ans,S,a[N][N],s[N][N];
int b[N],hL[N],hR[N],lL[N],lR[N];
void work_H()
{
for(int i=1;i<=200;++i)
{
int val=0;
memset(b,0,sizeof(b));
for(int j=i;j<=200;++j)
{
int sum=0,vl=0;
for(int k=1;k<=200;++k)
{
b[k]+=s[j][k];sum+=b[k];
if(sum<0) sum=0;
vl=max(vl,sum);
}
hL[i]=max(hL[i],vl);
val=max(val,vl);
}
hR[i]=max(hR[i],val);
}
}
void work_L()
{
for(int i=1;i<=200;++i)
{
int val=0;
memset(b,0,sizeof(b));
for(int j=i;j<=200;++j)
{
int sum=0,vl=0;
for(int k=l;k<=200;++k)
{
b[k]+=s[k][j];sum+=b[k];
if(sum<0) sum=0;
vl=max(vl,sum);
}
lL[i]=max(lL[i],vl);
val=max(val,vl);
}
lR[i]=max(lR[i],val);
}
}
void work()
{
for(int i=1;i<=200;++i) hL[i]=max(hL[i],hL[i-1]),lL[i]=max(lL[i],lL[i-1]);
for(int i=200;i;--i) hR[i]=max(hR[i],hR[i+1]),lR[i]=max(lR[i],lR[i+1]);
for(int i=1;i<=200;++i)
ans=max(ans,S+max(hL[i]+hR[i+1],lL[i]+lR[i+1]));
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,x,y,xx,yy;i<=n;++i)
{
scanf("%d %d %d %d",&x,&y,&xx,&yy);
a[x][y]++;
a[x][yy+1]--;
a[xx+1][y]--;
a[xx+1][yy+1]++;
}
for(int i=1;i<=200;++i)
for(int j=1;j<=200;++j)
{
a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
if(a[i][j]==m) s[i][j]=-1;
else if(a[i][j]==m-1) S++,s[i][j]=1;
}
//手动容斥
work_H();//枚举以行为界限的矩形
work_L();//枚举以列为界限的矩形
work();//更新最大的矩形!!!
printf("%d",ans);
}
伪二维实一维
问题 E: 【Ural 1028】数星星 Stars
【题目描述】
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。
例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。例图中有 1 个 0 级,2 个 1 级,1 个 2 级,1 个 3 级的星星。
给定星星的位置,输出各级星星的数目。
一句话题意:给定 n 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
【数据输入】第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
【数据输出】N 行,每行一个整数,分别是 0 级,1 级,2 级,……,N−1 级的星星的数目。
【输入样例】5
1 1
5 1
7 1
3 3
5 5
【输出样例】1
2
1
1
0
【数据范围】数据范围与提示:
对于全部数据,1≤N≤1.5×104, 0≤x,y≤3.2×104 。
将x或y任一先排序(本题已经排好),则可转为一维进行。
偷懒一开始没写离散化TLE了一个点,还是写上了。
#include<bits/stdc++.h>
using namespace std;
#define N 15005
int n,m,tot,c[N],cnt[N],s[N],t[N];
map<int,int>lsh;
void add(int x,int y)
{
for(;x<=tot;x+=x&-x) c[x]+=y;
}
int ask(int x)
{
int res=0;
for(;x;x-=x&-x) res+=c[x];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1,y;i<=n;++i)
scanf("%d %d",&t[i],&y),s[i]=t[i];
sort(s+1,s+n+1);
tot=unique(s+1,s+n+1)-s-1;
for(int i=1;i<=tot;++i) lsh[s[i]]=i;
for(int i=1;i<=n;++i)
{
cnt[ask(lsh[t[i]])]++;
add(lsh[t[i]],1);
}
for(int i=0;i<n;++i)
printf("%d\n",cnt[i]);
}
查询特定区间内不同的数的个数
将查询离线并按照右端点排序。
对于扫描到位置i时,由于此处查询操作都会查询到a[i]位置的数,则右端点为i左端点向前伸缩任意长度时,a[i]离右端点位置更近,a[i]能做出贡献时别的相同数值不同位置的数可能无法作出贡献,a[i]不能贡献时别的数一定不能贡献,故对于每个数值val,只在最后一个位置作出贡献1,其他位置贡献为0,再结合树状数组快速修改查询。
模板代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m,a[N],b[N],c[N],ans[N];
struct e_
{
int l,r,id;
friend bool operator<(e_ a,e_ b)
{
return a.r<b.r;
}
}e[N];
void add(int x,int y)
{
for(;x<=n;x+=x&-x) c[x]+=y;
}
int ask(int x)
{
int res=0;
for(;x;x-=x&-x) res+=c[x];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
scanf("%d",&m);
for(int i=1;i<=m;++i) scanf("%d %d",&e[i].l,&e[i].r),e[i].id=i;
sort(e+1,e+m+1);
for(int i=1,j=1;i<=n;++i)
{
if(b[a[i]]) add(b[a[i]],-1);
add(i,1);
b[a[i]]=i;
while(e[j].r==i) ans[e[j].id]=ask(i)-ask(e[j].l-1),j++;
}
for(int i=1;i<=m;++i) printf("%d\n",ans[i]);
}
变式例题1:
查询特定区间内出现了两次的数的个数。
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5;
int n,m,co,a[N],b[N][2],c[N],ans[N];
struct e_
{
int l,r,id;
friend bool operator<(e_ a,e_ b)
{
return a.r<b.r;
}
}e[N];
inline void add(int x,int y)
{
for(;x<=n;x+=x&-x) c[x]+=y;
}
inline int ask(int x)
{
int res=0;
for(;x;x-=x&-x) res+=c[x];
return res;
}
int main()
{
scanf("%d %d %d",&n,&co,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=m;++i) scanf("%d %d",&e[i].l,&e[i].r),e[i].id=i;
sort(e+1,e+m+1);
for(int i=1,j=1;i<=n;++i)
{
if(!b[a[i]][0]) b[a[i]][0]=i;
else if(!b[a[i]][1]) b[a[i]][1]=i,add(b[a[i]][0],1);
else add(b[a[i]][0],-1),add(b[a[i]][1],1),b[a[i]][0]=b[a[i]][1],b[a[i]][1]=i;
while(e[j].r==i) ans[e[j].id]=ask(i)-ask(e[j].l-1),j++;
}
for(int i=1;i<=m;++i) printf("%d\n",ans[i]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号