题解：CF1764C Doremy's City Construction

CF1764C Doremy's City Construction

题意

测试 \(T\) 次。

给定 \(n\) 个点，每个点有点权为 \(a_i\)，任意连边，使图中不存在有三点 \(u,v,w\) 同时存在边 \((u,v),(v,w)\) 和 \(a_u \leq a_v \leq a_w\)，输出最多连的边数。

数据范围：\(2 \leq n \leq 2 \times 10^5\)，\(\ 1 \leq a_i \leq 1 \times 10^6\)，保证每组测试样例中 \(n\) 的和不超过 \(2 \times 10^5\)。

思路

一个点不能同时与大于等于和小于等于他的点相连，因此，我们考虑二分图思想。

• 当点权不全部相等时：

将所有点分到两个集合 \(S_1,S_2\) 中去。令 \(S_1\) 中最大点权小于 \(S_2\) 中最小点权，之后使 \(S_1\) 中的每一个点与 \(S_2\) 中的每一个点相连，则边的个数为集合 \(S_1\) 中元素个数与集合 \(S_2\) 中元素个数之积，易得这是对于当下集合 \(S_1,S_2\) 的最优连边方案。

接下来枚举不同的 \(S_1,S_2\) 的分法，取整体最优解，如下图：

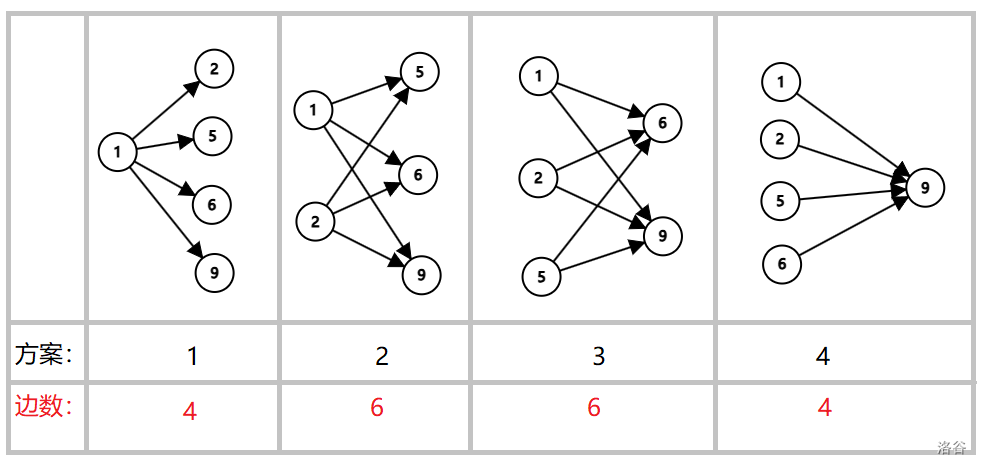
• 当点权全部相等时：

两两相连最优，答案为点数的一半，如图：

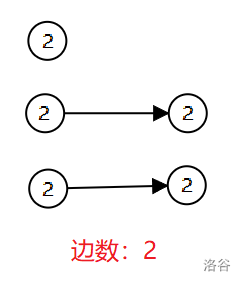
这是思路，更多详情请看代码。

代码

#include<bits/stdc++.h>
using namespace std;
long long n, a[200005], T;
int main() {
	scanf("%lld", &T);
	while (T--) {
		scanf("%lld", &n);
		long long max_ans = 0, S1_num = 1; //S1_num即表示S1中的数量也表示S1末尾元素下标
		for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
		sort(a + 1, a + n + 1); //排序方便分类
		if (a[1] == a[n]) { //判断点权是否全部相等
			cout << n / 2 << endl;
			continue;
		}
		while (S1_num < n) { //S1中点最多为n-1个
			while (S1_num < n && a[S1_num] == a[S1_num + 1]) S1_num++; //使与S1中最大点权一样的点加到S1中,如4,4两个点使捆绑的
			max_ans = max(max_ans, S1_num * (n - S1_num)); //乘法原理计算结果并打擂台
			S1_num++; //向S1中添加一个元素
		}
		cout << max_ans << endl;
	}
	return 0;
}

完结撒花！