题解：[ABC375C] Spiral Rotation

Spiral Rotation

题意：

有一个 \(n \times n\) 的矩阵，从最外层向内依次旋转 \(90 ^ \circ\)（旋转的是实心矩阵，也就是说包含其内部元素）。

图示如下：

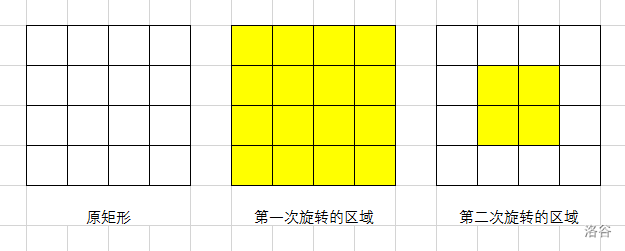
思路：

我们对每次旋转的矩阵的最外层进行讨论：从外向内数第 \(k\) 个外层会被它外面的 \(k-1\) 个外层连带旋转 \(k-1\) 次，那么它一共会旋转 \(k\) 次。这样我们就将旋转矩阵转换为了旋转一个外层。另外，最外层旋转 \(k\) 次等价于旋转 \(k \bmod 4\) 次，这样可以保证正确的时间复杂度。

旋转一个外层只需要复制一个辅助数组按顺序重新赋值即可。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
char c[3005][3005], cc[3005][3005];
ll n;
void solve(ll k) {
	memcpy(cc, c, sizeof(c)); //复制一份方便旋转 
	for(int i=k; i<=n-k+1; i++) c[i][n-k+1]=cc[k][i]; //上方->右方 
	for(int i=k; i<=n-k+1; i++) c[n-k+1][n-i+1]=cc[i][n-k+1]; //右方->下方 
	for(int i=k; i<=n-k+1; i++) c[i][k]=cc[n-k+1][i]; //下方->左方 
	for(int i=k; i<=n-k+1; i++) c[k][n-i+1]=cc[i][k]; //左方->上方 
}
int main() {
	cin >> n;
	for(int i=1; i<=n; i++) for(int j=1; j<=n; j++) cin >> c[i][j];
	for(int k=1; k<=n/2; k++) for(int j=1; j<=k%4; j++) solve(k);
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) cout << c[i][j];
		puts("");
	}
	return 0;
}