LeetCode系列之数学专题

1. 数学题目概述

https://leetcode-cn.com/tag/math/

2. 典型题目

2.1 最小好进制

https://leetcode-cn.com/problems/smallest-good-base/

2.2 罗马数字转整数

https://leetcode-cn.com/problems/roman-to-integer/

需要注意的规则：

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

    I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
    X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
    C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

所以，按照我的理解，IVX这种，属于非法的罗马数字。

int romanToInt(string s) {
    int res = romanDigits.at(s[0]);
    for (int i = 1; i < s.size(); i++) {
        int pre = romanDigits.at(s[i - 1]);
        int cur = romanDigits.at(s[i]);
        if (cur <= pre) {
            res += cur;
        } else {
            res += (cur - 2 * pre);
        }
    }
    return res;
}

const std::unordered_map<char, int> romanDigits = {
    {'I', 1},
    {'V', 5},
    {'X', 10},
    {'L', 50},
    {'C', 100},
    {'D', 500},
    {'M', 1000},
};

时间复杂度O(N)，空间复杂度O(1)。

2.3 整数翻转

https://leetcode-cn.com/problems/reverse-integer/

int reverse(int x) {
    int rev = 0;
    while (x != 0) {
        int pop = x % 10;
        x /= 10;
        if (rev > INT_MAX/10 || (rev == INT_MAX / 10 && pop > 7)) return 0;
        if (rev < INT_MIN/10 || (rev == INT_MIN / 10 && pop < -8)) return 0;
        rev = rev * 10 + pop;
    }
    return rev;
}

方法很巧妙，但是一定要注意防止溢出。

INT_MAX = 2³¹ - 1 = 2,147,483,647；INT_MIN = -2³¹ = -2,147,483,648

据此给出判断溢出的条件。

时间复杂度O(1)，空间复杂度O(1)。

个人认为官方解答里的时间复杂度分析的不对，位数不会超过32位，所以时间复杂度小于一个常数，应该是O(1)。

2.4 快乐数

https://leetcode-cn.com/problems/happy-number/

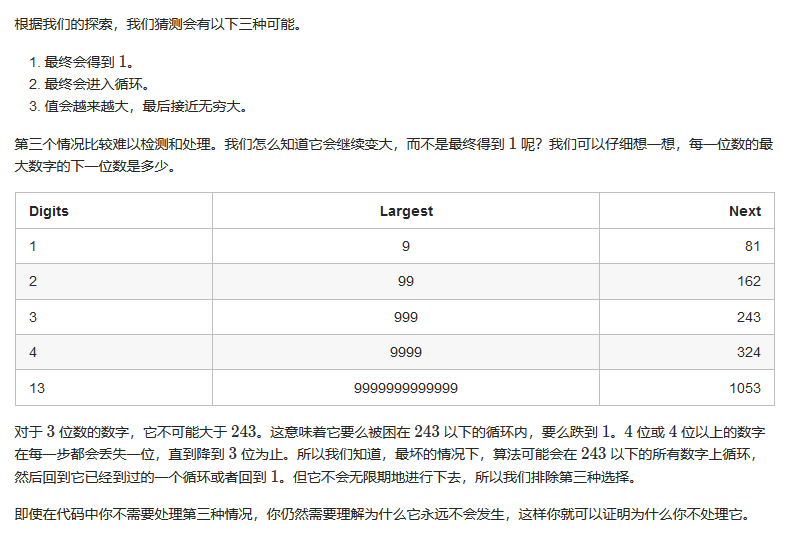
两种解法比较常见：hashset检测循环、快慢指针检测循环

还有一种更逆天的数学解法（其实看题目的时候，我就意识到会有这么一种解法的，只是没想出来）

bool isHappy(int n) {
    while (n != 1 && cycleMembers.find(n) == cycleMembers.end()) {
        n = getNextN(n);
    }
    return n == 1;
}

int getNextN(int n) {
    int sum = 0;
    while (n != 0) {
        int oneDigital = n % 10;
        n = n / 10;
        sum += oneDigital * oneDigital;
    }
    return sum;
}
const unordered_set<int> cycleMembers = {4, 16, 37, 58, 89, 145, 42, 20};

先用暴力法计算出所有可能的循环数，然后判断 Next N 是否出现在了这个循环里。

时间复杂度O(log n)，空间复杂度O(1)。

2.5 x的平方根

https://leetcode-cn.com/problems/sqrtx/

2.6 两数相加

https://leetcode-cn.com/problems/add-two-numbers/

2.7 阶乘后的零

https://leetcode-cn.com/problems/factorial-trailing-zeroes/

宗旨是计算阶乘中5的个数，因为2的个数远大于5的个数，所以5的个数决定了10的个数，也即末尾零的个数。

下面的方法，对找5的个数进行了相当大的改进。

int trailingZeroes(int n) {
    int c5 = 0;
    int64_t power5 = 5;
    while (n >= power5) {
        c5 += n / power5;
        power5 *= 5;
    }
    return c5;
}

时间复杂度O(log n)，空间复杂度O(1)。

2.8 excel表列序号

https://leetcode-cn.com/problems/excel-sheet-column-number/

2.9 二进制求和

https://leetcode-cn.com/problems/add-binary/

2.10 各位相加

https://leetcode-cn.com/problems/add-digits/

3. 总结