CF1494D Dogeforces

又是一个反问题。

而且是重建类的问题（Restoring Map，永远的神）。

给你一棵树，满足父节点的数值>子节点的数值。

现在给你叶子的数量和数值，以及它们两两配对的lca的数值。

总之，找到能够限制性非常强的必要条件，是构造题的入口。

因为总的数量没限制，所以我们对每个配对都直接构造一个lca加在这两个点上方？

不行哦。

既然数值具有单调性，那么我们从底层开始加lca的话，就是从lca的数值小的开始放置。

当一些点加了lca后连通了，我们可以考虑整个连通块，也就是子树，用它的根来表示。

以后，对于配对(x,y)，我们只要找u=x所在子树的root，v=y所在子树的root，然后在这两个u,v上面添加一个lca。

这样的添加方式，对于之前处理过的配对(x,y)，后面的添加不会影响前面的配对的lca。

而新的需求又被满足了，所以是做出来了？（脑中AC）

 

最终树高、树size的大小会是怎样？

如果每个配对都添加一个新点，那么最后点数最多O(N^2)

树高最多O(N)

总复杂度O(N^3)，可以接受，但是这难度也不至于上2000吧。

怀疑我哪儿没理解到位。

这样构造出来的非叶子节点也至少有两个子节点，没问题。

 

唯一可能出错的情况，就目前我想到的是，配对(x,y)已经处在一个连通块中了，但是其lca不是我们想要的。

这种情况可能出现吗、

 

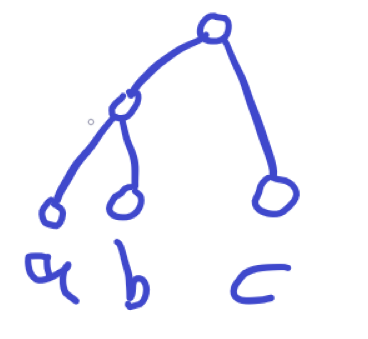
比如我们先处理(a,b)，然后处理(a,c)，得到上面的图，但是接下来处理(b,c)，发现已经连通了，而lca却不是我们想要的。

咋办？或者可以在现有的root上再加一个fa，但是这可能会破坏每个非叶子节点都至少有两个子节点的性质。

那这样感觉不是所有数据都有解啊。

那就理解为题目数据保证有解。