HCCF论文阅读笔记
Abstract
存在的挑战:
- 使用更深层次的基于图的CF架构有过平滑效应,会导致难以区分的用户表示和推荐结果的退化
- 监督信号在现实中是稀疏和偏态分布的,限制了CF范式的表达能力
提出了一种新的自监督框架超图对比协同过滤(HCCF),通过一个超图增强的交叉视图对比学习架构来联合捕获局部和全局协作的关系
优点:设计的超图结构提高了基于GNN的CF范式的识别能力,从而全面捕获用户之间复杂的高阶关系
Introduction
现有的模型有两个关键问题还没有被探索
- 过平滑协同影响:具有更深的嵌入传播层的图神经CF架构可能会导致难以区分的用户向量,这个限制了高阶协作关系的表示质量。连接用户/项目之间的信息在其交互子图上的过度混合可能涉及到对唯一用户偏好表示的噪声。所以从整体交互图中编码可区分的和信息丰富的用户/项目表示对于区分用户偏好至关重要
- 监督交互数据的稀缺性和噪声
于是提出了一种新的模型HCCF,开发了一个基于神经网络结构的协同关系建模的超图学习对比框架。利用超图学习架构,以基于低秩结构学习的全局协同效应来补充基于图的CF范式的编码
目前的使用超图来编码推荐中的高阶关系,但是大多数研究依赖于用户或项目之间的原始连接来生成他们的超图连接。但是这种观察到的连接是有噪声或者不完整的。为了缓解这个问题,在HCCF中,我们共同学习了参数化的超图引导的用户依赖结构和原始的交互图编码器,以获得更好的用户偏好表示
此外还设计了基于对偶图对比学习的关系学习增强模式,目前的数据增强会丢失一些基本信息,所以我们将显式交互图和学习到的隐式超图结构视为两个对比视图,而不考虑基于预定义算子的随机噪声扰动
本文的贡献:
- 引入了一个通用的自监督学习框架,通过增强图协同过滤范式的鲁棒性,通过在局部和全局协同效应建模之间提取自增强的对比视图
- 提出了将全局超图结构学习和局部协同关系编码器集成的HCCF,以相互协同监督。设计的超图对比学习模式增强了图神经CF范式,以有效的实例识别来捕捉用户和项目之间的内在的和内隐的依赖性
Method
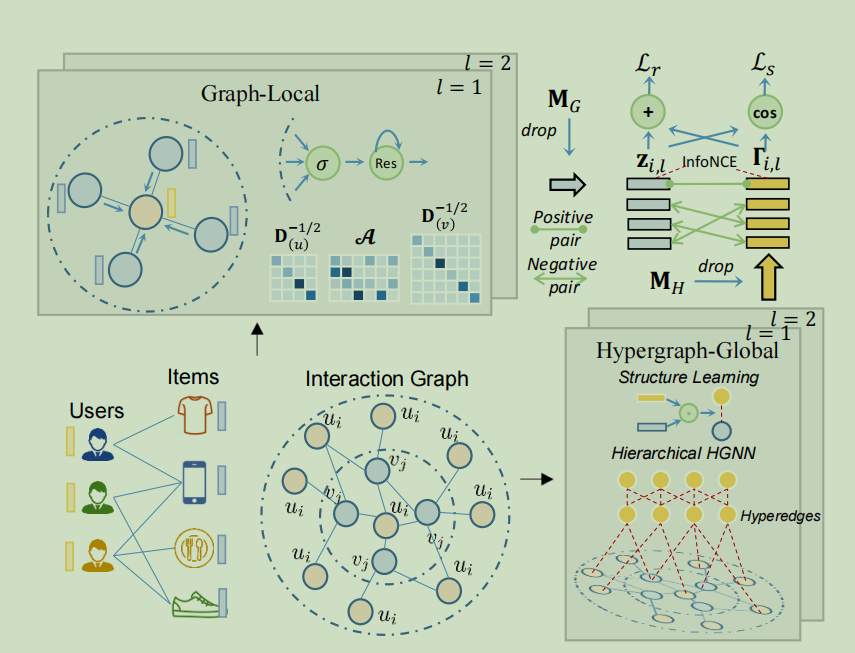
模型的整体流程如下:
首先利用图的消息传递模块作为编码器来捕获用户和项目之间的局部协作相似性
然后提出一种新的具有全局依赖的超图神经网络来全面捕获图神经CF范式的全局协同效应
最后引入一种新的具有互补的自蒸馏视图(局部和全局协作关系)的超图对比学习
下面是模型主要方法的具体细节
Local Collaborative Relation Encoding
设计局部嵌入传播层
\(\mathbf{z}_{i}^{(u)}=\sigma(\bar{\mathcal{A}}_{i,*}\cdot\mathbf{E}^{(v)}),\quad\mathbf{z}_{j}^{(v)}=\sigma(\bar{\mathcal{A}}_{*,j}\cdot\mathbf{E}^{(u)})\)
\(\bar{\mathcal{A}}\)就是标准化的用户-项目交互矩阵
消息传递的过程如下:
\(\mathbf e_{i,l}^{(u)}=\mathbf z_{i,l}^{(u)}+\mathbf e_{i,l-1}^{(u)},\quad\mathbf e_{j,l}^{(v)}=\mathbf z_{j,l}^{(v)}+\mathbf e_{j,l-1}^{(v)}\)
Hypergraph Global Dependency Learning
通过超图结构设计一个全局依赖编码器
Hypergraph Message Passing Paradigm
将用户和项目的超图依赖定义为\(\mathcal{H}^{(u)},\mathcal{H}^{(v)}\),超图消息传递的正式表示为:
\(\Gamma_l^{(u)}=\sigma(\mathcal{H}^{(u)}\Lambda^{(u)})=\sigma(\mathcal{H}^{(u)}\cdot\mathcal{H}^{(u)\top}\cdot{E}_{l-1}^{(u)})\)
其中,\(\Lambda^{(u)}\)表示用户的特定超边嵌入,\(\Gamma_l^{(u)}\)表示第l层的超图表示空间的用户超嵌入
超图消息提取阶段需要用户/项目嵌入和可学习的超图依赖矩阵计算输入知识,共同维持局部和全局的协作效果
Parameterized Hypergraph Structure Learning
为了自适应地学习跨用户和项目的基于超图的依赖结构,提出了对超图依赖矩阵\(\mathcal{H}^{(u)},\mathcal{H}^{(v)}\)进行参数化,它们与基于GNN的CF架构联合优化
但是学习密集超图邻接矩阵的计算成本很高,为了解决这个问题,提出了将超图结构矩阵以低秩的方式参数化为隐空间中,来实现模型的效率
\(\mathcal{H}^{(u)}=\mathbf{E}^{(u)}\cdot\mathbf{W}^{(u)},\quad\mathcal{H}^{(v)}=\mathbf{E}^{(v)}\cdot\mathbf{W}^{(v)}\)
W表示可学习的嵌入矩阵,E表示用户/项目的嵌入
此外还设计了基于H的矩阵分解的参数化依赖结构编码器,进一步正则化了隐结构学习以缓解过拟合
Hierarchical Hypergraph Mapping
为了进一步用高水平的超边特征交互来增强超图神经架构,所以通过叠加大小为H的不同超边层来增加多个超图神经层来增强HCCF
上述的超边集将作为第一个超图层,它将与深度超图层非线性地交互,在形式上,通过编码函数\(\psi(\cdot)\)来推导深层的超边嵌入
\(\bar{\boldsymbol{\Lambda}}=\psi^{\boldsymbol{c}}(\boldsymbol{\Lambda}),\psi(\boldsymbol{X})=\sigma(\mathbf{V}\mathbf{X})+\mathbf{X},\boldsymbol{\Lambda}=\mathcal{H}^{\top}\mathbf{E}\)
c表示超图嵌入层的数量,V是用于嵌入投影的可训练参数矩阵
在分层超图映射之后,我们对用户/项目表示进行细化
\(\Gamma_{l}=\sigma(\mathcal{H}\cdot\bar{\Lambda})=\sigma(\mathcal{H}\cdot\psi^{\mathsf{c}}(\mathcal{H}^{\top}\cdot\mathbf{E}))\)
Multi-Order Aggregation and Prediction
为了将局部依赖编码与全局协同关系建模相结合,我们迭代的执行图的局部嵌入传播和超图信息聚合
\(\mathbf{e}_{i,l}^{(u)}=\mathbf{z}_{i,l}^{(u)}+\Gamma_{i,l}^{(u)}+\mathbf{e}_{i,l-1}^{(u)},\mathbf{e}_{j,l}^{(v)}=\mathbf{z}_{j,l}^{(v)}+\Gamma_{j,l}^{(v)}+\mathbf{e}_{j,l-1}^{(v)}\)
然后进一步将残差操作应用于嵌入聚合,形式如下:
\(\Psi_{i}^{(u)}=\sum_{l=0}^{L}\mathbf{E}_{i,l}^{(u)},\Psi_{j}^{(v)}=\sum_{l=0}^{L}\mathbf{E}_{j,l}^{(v)},\mathrm{Pr}_{i,j}=\boldsymbol{\Psi}_{i}^{(u)\top}\boldsymbol{\Psi}_{j}^{(v)}\)
之后的Loss函数如下:
\(\begin{aligned}\mathcal{L}_r&=\sum_{i=0}^I\sum_{s=1}^S\max(0,1-\Pr_{i,p_s}+\Pr_{i,n_s})\end{aligned}\)
对于每个用户,我们分别从观察到的和没有交互的项目中抽取阳性和阴性实例
Hypergraph-enhanced Contrastive Learning
本节描述了如何在超图神经架构下使用交叉视图协同监督信号来实现HCCF
Hypergraph-guided Contrasting
通过最大化显式用户-项目交互关系和隐式基于超图依赖关系的一致性来进行对比学习的设计,也就是生成两个视图来进行对比学习,分别是用户-项目交互图上的局部协作关系编码以及用户/项目之间的全局超图结构学习
Cross-View Collaborative Supervision
这部分主要介绍损失函数,采用InfoNCE
\(\mathcal{L}_s^{(u)}=\sum_{i=0}^I\sum_{l=0}^L-\log\frac{\exp(s(\mathbf{z}_{i,l}^{(u)},\Gamma_{i,l}^{(u)})/\tau)}{\sum_{l^{\prime}=0}^I\exp(s(\mathbf{z}_{i,l}^{(u)},\Gamma_{i^{\prime},l}^{(u)})/\tau)}\)
Data Augmentation on Graph Structure
为了进一步缓解交叉视图对比学习过程中的过拟合问题,我们在用户-项目交互图和学习到的超图结构上设计了edge dropout 算子
\(\bar{\mathcal{A}}:=\mathbf{M}_{G}\circ\bar{\mathcal{A}};\quad\mathcal{H}:=\mathbf{M}_{H}\circ\mathcal{H}\)
其中M是带有dropout概率的的二进制掩码矩阵
最终整体模型的损失函数为:
\(\mathcal{L}=\mathcal{L}_{r}+\lambda_{1}\cdot(\mathcal{L}_{s}^{(u)}+\mathcal{L}_{s}^{(v)})+\lambda_{2}\cdot\|\Theta\|_{\mathrm{F}}^{2}\)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号