P3973 [TJOI2015]线性代数

【题意】

 

 

 

 

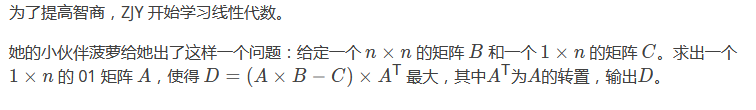
【分析】

这是一个很妙的题

考虑到A只能是0/1，所以又回归到了二者选其一的模型

 

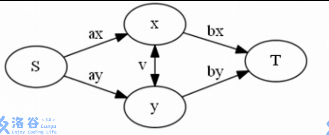
利用这种最小割的模型，去解一个方程组，算出合适的边权即可

 

 【代码】

#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define fi first
#define se second
#define lson now<<1
#define rson now<<1|1
typedef long long ll;
const int maxn=500*501+5;
const int maxm=1000005;
int n,m,a[maxn],b[maxn];
int S,T;
const ll inf=1e17;
int head[maxn],tot=1,cur[maxn];
struct edge
{
    int to,nxt;
    ll v;
}e[maxm<<1];
void add(int x,int y,ll z)
{
    e[++tot].to=y; e[tot].nxt=head[x]; e[tot].v=z; head[x]=tot;
    e[++tot].to=x; e[tot].nxt=head[y]; e[tot].v=0; head[y]=tot;
}
int dep[maxn];
bool bfs()
{
    for(int i=S;i<=T;i++)
        dep[i]=-1,cur[i]=head[i];
    // memset(dep,-1,sizeof(dep));
    // memcpy(cur,head,sizeof(cur));
    queue <int> q;
    dep[S]=0;
    q.push(S);
    while(!q.empty())
    {
        int u=q.front(); q.pop();
        for(int i=head[u];i;i=e[i].nxt)
        {
            int to=e[i].to;
            if(dep[to]!=-1 || !e[i].v) continue;
            q.push(to);
            dep[to]=dep[u]+1;
        }
    }
    return (dep[T]!=-1);
}
ll dfs(int u,ll flow)
{
    if(u==T) return flow;
    ll res=0;
    for(int &i=cur[u];i;i=e[i].nxt)
    {
        int to=e[i].to;
        if(dep[to]!=dep[u]+1 || e[i].v<=0) continue;
        ll tmp=dfs(to,min(e[i].v,flow));
        flow-=tmp; res+=tmp;
        e[i].v-=tmp; e[i^1].v+=tmp;
        if(!flow) break;
    }
    if(!res) dep[u]=-1;
    return res;
}
ll ans;
ll dinic()
{
    ll ans=0;
    while(bfs())
    {
        ans+=dfs(S,inf);
    }
    return ans;
}
int gcd(int x,int y)
{
    if(!y) return x;
    return gcd(y,x%y); 
}
int main()
{

    scanf("%d",&n);
    ll sum=0,x;
    S=0; T=n*n+n+1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            scanf("%lld",&x);
            sum+=x;
            add(S,(i-1)*n+j,x);
            add((i-1)*n+j,n*n+i,inf);
            add((i-1)*n+j,n*n+j,inf);
        }
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&x);
        add(n*n+i,T,x);
    }
    printf("%lld",sum-dinic());
    return 0;
}