数据结构 二叉树遍历

我们使用python 代码来生成一个二叉树遍历图例
在代码中依次输入的前序遍历

# input
Enter preorder traversal (space-separated, use 'None' for null nodes): 1 2 4 None None 5 None None 3 6 None None 7 None None

代码如下：

import matplotlib.pyplot as plt

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def build_tree_from_preorder(preorder):
    if not preorder:
        return None
    
    root_value = preorder.pop(0)
    if root_value is None:
        return None
    
    root = Node(root_value)
    root.left = build_tree_from_preorder(preorder)
    root.right = build_tree_from_preorder(preorder)
    return root

def plot_tree(node, x, y, dx, dy, ax):
    if node:
        ax.text(x, y, str(node.value), style='italic', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
        if node.left:
            ax.plot([x, x - dx], [y, y - dy], 'k-')
            plot_tree(node.left, x - dx, y - dy, dx / 2, dy, ax)
        if node.right:
            ax.plot([x, x + dx], [y, y - dy], 'k-')
            plot_tree(node.right, x + dx, y - dy, dx / 2, dy, ax)

def main():
    # 输入前序遍历数组
    preorder_input = input("Enter preorder traversal (space-separated, use 'None' for null nodes): ")
    preorder = []
    for value in preorder_input.split():
        if value.lower() == 'none':
            preorder.append(None)
        else:
            preorder.append(int(value))
    
    # 构建二叉树
    root = build_tree_from_preorder(preorder)
    
    # 输出前序遍历结果
    print("Preorder Traversal:", preorder)
    
    # 绘制树结构
    fig, ax = plt.subplots()
    plot_tree(root, 0, 0, 100, 100, ax)
    ax.set_aspect('equal')
    ax.axis('off')
    plt.show()

if __name__ == "__main__":
    main()

# output
Preorder Traversal: [1, 2, 4, None, None, 5, None, None, 3, 6, None, None, 7, None, None]

# input
Enter preorder traversal (space-separated, use 'None' for null nodes): 1 None 2 None 3 None 4
# output
Preorder Traversal: [1, None, 2, None, 3, None, 4]
  1
   \
    2
     \
      3
       \
        4

Enter preorder traversal (space-separated, use 'None' for null nodes): 1 2 None None 3 4 None None 5 None None
Preorder Traversal: [1, 2, None, None, 3, 4, None, None, 5, None, None]

      1
     / \
    2   3
       / \
      4   5

中序遍历

import matplotlib.pyplot as plt

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def build_balanced_tree_from_inorder(inorder):
    """根据中序遍历数组构建平衡二叉树"""
    if not inorder:
        return None
    
    mid = len(inorder) // 2
    root = Node(inorder[mid])
    
    root.left = build_balanced_tree_from_inorder(inorder[:mid])
    root.right = build_balanced_tree_from_inorder(inorder[mid+1:])
    
    return root

def plot_tree(node, x, y, dx, dy, ax):
    """递归绘制树结构"""
    if node:
        ax.text(x, y, str(node.value), style='italic', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
        if node.left:
            ax.plot([x, x - dx], [y, y - dy], 'k-')
            plot_tree(node.left, x - dx, y - dy, dx / 2, dy, ax)
        if node.right:
            ax.plot([x, x + dx], [y, y - dy], 'k-')
            plot_tree(node.right, x + dx, y - dy, dx / 2, dy, ax)

def main():
    # 输入中序遍历数组
    inorder_input = input("Enter inorder traversal (space-separated): ")
    inorder = list(map(int, inorder_input.split()))
    
    # 构建平衡二叉树
    root = build_balanced_tree_from_inorder(inorder)
    
    # 输出中序遍历结果（验证）
    print("Inorder Traversal (验证):", inorder_traversal(root))
    
    # 绘制树结构
    fig, ax = plt.subplots()
    plot_tree(root, 0, 0, 100, 100, ax)
    ax.set_aspect('equal')
    ax.axis('off')
    plt.show()

def inorder_traversal(root):
    """中序遍历（用于验证）"""
    if not root:
        return []
    return inorder_traversal(root.left) + [root.value] + inorder_traversal(root.right)

if __name__ == "__main__":
    main()

# output
Enter inorder traversal (space-separated): 4 2 5 1 6 3 7

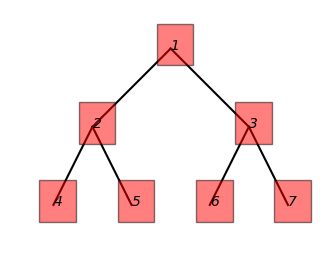
# 根据前序遍历和后序遍历输出中序遍历
# 注意：根据前序遍历和后序遍历无法唯一确定一棵二叉树，因此需要假设树是一棵满二叉树（每个节点都有 0 或 2 个子节点）。以下代码基于此假设实现
import matplotlib.pyplot as plt

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def build_tree_from_preorder_postorder(preorder, postorder):
    if not preorder or not postorder:
        return None
    
    root_value = preorder[0]
    root = Node(root_value)
    
    if len(preorder) == 1:
        return root
    
    left_root_value = preorder[1]
    left_root_idx = postorder.index(left_root_value)
    
    root.left = build_tree_from_preorder_postorder(preorder[1:left_root_idx+2], postorder[:left_root_idx+1])
    root.right = build_tree_from_preorder_postorder(preorder[left_root_idx+2:], postorder[left_root_idx+1:-1])
    
    return root

def inorder_traversal(root):
    if not root:
        return []
    return inorder_traversal(root.left) + [root.value] + inorder_traversal(root.right)

def plot_tree(node, x, y, dx, dy, ax):
    if node:
        ax.text(x, y, str(node.value), style='italic', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
        if node.left:
            ax.plot([x, x - dx], [y, y - dy], 'k-')
            plot_tree(node.left, x - dx, y - dy, dx / 2, dy, ax)
        if node.right:
            ax.plot([x, x + dx], [y, y - dy], 'k-')
            plot_tree(node.right, x + dx, y - dy, dx / 2, dy, ax)

def main_preorder_postorder():
    preorder_input = input("Enter preorder traversal (space-separated): ")
    postorder_input = input("Enter postorder traversal (space-separated): ")
    
    preorder = list(map(int, preorder_input.split()))
    postorder = list(map(int, postorder_input.split()))
    
    if len(preorder) == len(postorder) and len(preorder) > 0:
        root = build_tree_from_preorder_postorder(preorder, postorder)
        print("Inorder traversal:", inorder_traversal(root))

        fig, ax = plt.subplots()
        plot_tree(root, 0, 0, 100, 100, ax)
        ax.set_aspect('equal')
        ax.axis('off')
        plt.show()
    else:
        print("Invalid input: Preorder and postorder traversals must have the same length and not be empty.")

if __name__ == "__main__":
    main_preorder_postorder()

# input
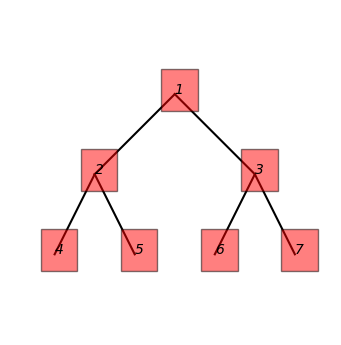
Enter preorder traversal (space-separated): 1 2 4 5 3 6 7
Enter postorder traversal (space-separated): 4 5 2 6 7 3 1
# output
Inorder traversal: [4, 2, 5, 1, 6, 3, 7]

# 根据中序遍历和后序遍历输出前序遍历
import matplotlib.pyplot as plt

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def build_tree_from_inorder_postorder(inorder, postorder):
    if not inorder or not postorder:
        return None
    
    root_value = postorder[-1]
    root = Node(root_value)
    
    mid_idx = inorder.index(root_value)
    
    root.left = build_tree_from_inorder_postorder(inorder[:mid_idx], postorder[:mid_idx])
    root.right = build_tree_from_inorder_postorder(inorder[mid_idx+1:], postorder[mid_idx:-1])
    
    return root

def preorder_traversal(root):
    if not root:
        return []
    return [root.value] + preorder_traversal(root.left) + preorder_traversal(root.right)

def plot_tree(node, x, y, dx, dy, ax):
    if node:
        ax.text(x, y, str(node.value), style='italic', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
        if node.left:
            ax.plot([x, x - dx], [y, y - dy], 'k-')
            plot_tree(node.left, x - dx, y - dy, dx / 2, dy, ax)
        if node.right:
            ax.plot([x, x + dx], [y, y - dy], 'k-')
            plot_tree(node.right, x + dx, y - dy, dx / 2, dy, ax)

def main_inorder_postorder():
    inorder_input = input("Enter inorder traversal (space-separated): ")
    postorder_input = input("Enter postorder traversal (space-separated): ")
    
    inorder = list(map(int, inorder_input.split()))
    postorder = list(map(int, postorder_input.split()))
    
    if len(inorder) == len(postorder) and len(inorder) > 0:
        root = build_tree_from_inorder_postorder(inorder, postorder)
        print("Preorder traversal:", preorder_traversal(root))
        
        fig, ax = plt.subplots()
        plot_tree(root, 0, 0, 100, 100, ax)
        ax.set_aspect('equal')
        ax.axis('off')
        plt.show()        
    else:
        print("Invalid input: Inorder and postorder traversals must have the same length and not be empty.")

if __name__ == "__main__":
    main_inorder_postorder()

Enter inorder traversal (space-separated): 4 2 5 1 6 3 7
Enter postorder traversal (space-separated): 4 5 2 6 7 3 1
Preorder traversal: [1, 2, 4, 5, 3, 6, 7]

# 根据中序遍历和前序遍历输出后序遍历
import matplotlib.pyplot as plt

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def build_tree(preorder, inorder):
    if not preorder or not inorder:
        return None
    
    root_value = preorder[0]
    root = Node(root_value)
    
    mid_idx = inorder.index(root_value)
    
    root.left = build_tree(preorder[1:mid_idx+1], inorder[:mid_idx])
    root.right = build_tree(preorder[mid_idx+1:], inorder[mid_idx+1:])
    
    return root

def postorder_traversal(root):
    if not root:
        return []
    return postorder_traversal(root.left) + postorder_traversal(root.right) + [root.value]

def plot_tree(node, x, y, dx, dy, ax):
    if node:
        ax.text(x, y, str(node.value), style='italic', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
        if node.left:
            ax.plot([x, x - dx], [y, y - dy], 'k-')
            plot_tree(node.left, x - dx, y - dy, dx / 2, dy, ax)
        if node.right:
            ax.plot([x, x + dx], [y, y - dy], 'k-')
            plot_tree(node.right, x + dx, y - dy, dx / 2, dy, ax)

def main():
    preorder_input = input("Enter preorder traversal (space-separated): ")
    inorder_input = input("Enter inorder traversal (space-separated): ")
    
    preorder = list(map(int, preorder_input.split()))
    inorder = list(map(int, inorder_input.split()))
    
    if len(preorder) == len(inorder) and len(preorder) > 0:
        root = build_tree(preorder, inorder)
        print("Postorder traversal:", postorder_traversal(root))
        
        fig, ax = plt.subplots()
        plot_tree(root, 0, 0, 100, 100, ax)
        ax.set_aspect('equal')
        ax.axis('off')
        plt.show()
    else:
        print("Invalid input: Preorder and inorder traversals must have the same length and not be empty.")

if __name__ == "__main__":
    main()

# input
Enter preorder traversal (space-separated): 1 2 4 5 3 6 7
Enter inorder traversal (space-separated): 4 2 5 1 6 3 7
# output
Postorder traversal: [4, 5, 2, 6, 7, 3, 1]