python的Numpy库操作矩阵

原文链接

一、标量、向量、矩阵、张量

import numpy as np
#向量、张量、标量、矩阵
s = 5;
v = np.array([1,2]);
m = np.array([[1,2],[3,4]]);
t = np.array([[[1,2,3],[4,5,6],[7,8,9]],[[11,12,13],[14,15,16],[17,18,19]],[[21,22,23],[24,25,26],[27,28,29]]]);
print("标量"+str(s));
print("向量"+str(v));
print("矩阵"+str(m));
print("张量"+str(t));

二、矩阵转置

#矩阵的转置
m_t = m.transpose();
print("矩阵的转置"+str(m_t));

三、矩阵加法

#矩阵的相加
m_sum = m + m_t;
3 print("矩阵的相加"+str(m_sum));

四、矩阵乘法

#矩阵的乘法
m_mutiply = np.dot(m_t,m);#矩阵的乘法
m_mutiply = m_t.dot(m);#矩阵乘法
m_muti = np.mutiply(m,m_t);#逐元素相乘
m_muti1 = m*m_t;#逐元素相乘
print("矩阵相乘"+str(m_mutiply));
print("逐元素相乘"+str(m_muti)+"第二种"+str(m_muti1));

五、单位矩阵

#单位矩阵
matrix_danwei = np.identity(3);
print("单位矩阵"+str(matrix_danwei));

六、矩阵的逆

#矩阵的逆
A = [[1,2],[3,4]];
A_inv = np.linalg.inv(A);
print("A的逆矩阵"+str(A_inv));

七、矩阵范数

#矩阵的范数，机器学习使用的是F范数
arr = np.array([1,3]);
arr_two_norm = np.linalg.norm(arr,ord=2);#向量2范数
arr_one_norm = np.linalg.norm(arr,ord=1);#向量1范数
arr_inf_norm = np.linalg.norm(arr,ord=np.inf);#向量无穷范数
arr_matrix = np.array([[1,2],[3,4]]);
arr_matrix__frobenius_norm = np.linalg.norm(arr_matrix,ord="fro");#矩阵的F范数

八、特征值分解

#特征值分解
A_matrix = np.array([[1,2,3],[4,5,6],[7,8,9]]);
A_matrix_Eigen = np.linalg.eigvals(A)#计算特征值
eigvals,eigvectors = np.linalg.eig(A_matrix); #特征值：eigvals 特征向量：eigvectors

九、奇异值分解

#奇异值分解
A1_matrix = np.array([[1,2,3],[4,5,6]]);
U,D,V = np.linalg.svd(A);#U是左奇异向量  V是右奇异向量  D是对角矩阵，对角元素是A的奇异值

十、PCA降维

　　1、关于PCA降维，请移步

 

 

　　根据步骤写出PCA，并且保存至pca_file.py文件中

import numpy as np 
class PCA():
    def __init__(self):#构造函数
        pass#只做占位符，不执行任何操作
    def fit(X,n_components):
        n_samples = np.shape(X)[0] #得到矩阵X的行数
        covariance_matrix = (1/(n_samples-1))*(X-X.mean(axis=0)).T.dot(X - X.mean(axis=0))
        #对协方差矩阵进行特征值分解
        eigenvalues,eigenvectors = np.linalg.eig(covariance_matrix)
        #对特征值（特征向量）从大到小排序
        idx = eigenvalues.argsort()[::-1]
        eigenvalues = eigenvalues[idx][:n_components]
        eigenvectors = np.atleast_1d(eigenvectors[:,idx])[:,:n_components]
        #得到低维表示
        X_transformed = X.dot(eigenvectors)
        return X_transformed

　　2、使用定义的类对鸢尾花（iris）进行PCA降维，关于鸢尾花详细信息，请移步

　　　　

import pandas as pd
import numpy as np 
from sklearn.datasets import load_iris 
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import pca_file
import xlwt

#载入iris数据，展示PCA的使用
iris = load_iris()

#将鸢尾花数据记录到本地excel中查看
f = xlwt.Workbook()  # 创建工作簿
sheet1 = f.add_sheet(u'sheet1', cell_overwrite_ok=True)  # 创建sheet
[h, l] = iris.data.shape  # h为行数，l为列数
for i in range(h):
    for j in range(l):
        sheet1.write(i, j, iris.data[i, j])
f.save("C:\\Users\\25626\\Desktop\\PCA\\data.xls")
print("花卉类型"+str(iris.target_names)+str(iris.target))

#将iris数据记录到DataFrame表格
df = pd.DataFrame(iris.data,columns = iris.feature_names)
print("数据名称"+str(iris.feature_names))
df['label'] = iris.target
df.columns = ['sepal length','sepal width','petal length','petal width','label']
df.label.value_counts()
#查看数据
df.tail()
#查看数据
X = df.iloc[:,0:4]
y = df.iloc[:,4]
print("查看第一个数据：\n",X.iloc[0,0:4])
print("查看第一个标签：\n",y.iloc[0])

#使用PCA降维
model = pca_file.PCA
Y = model.fit(X,2)
principalDf = pd.DataFrame(np.array(Y),columns = ['principal component1','principal component2'])
Df = pd.concat([principalDf,y],axis=1)

#画图显示
fig = plt.figure(figsize = (5,5,))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1',fontsize = 15)
ax.set_ylabel('Principal Component 2',fontsize = 15)
ax.set_title("2 component PCA",fontsize = 20)
targets = [0,1,2]
colors = ['r','g','b']
for target,color in zip(targets,colors):
    indicesToKeep = Df['label'] == target
    ax.scatter(Df.loc[indicesToKeep,'principal component1'],Df.loc[indicesToKeep,'principal component2'],c = color,s =50)
ax.legend(targets)
ax.grid()  
plt.show()  

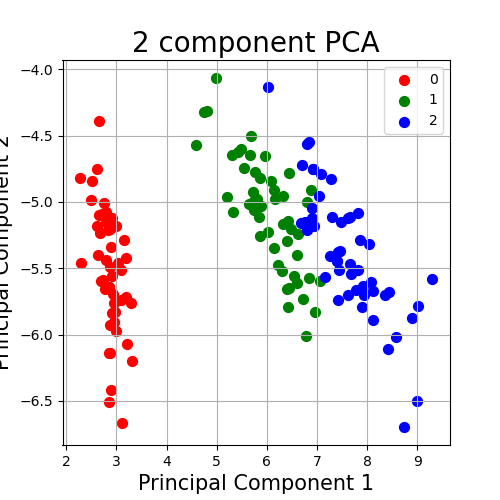
　　　　降维后数据如图所示