复杂度

大O记法

  我们需要一个不用具体的测试数据和测试环境，就可以粗略地估计算法执行效率的方法。这个方法我们称作复杂度，我们称作为大O记法。

时间复杂度

我们使用步数作为时间复杂度的计算，什么叫步数，可以简单理解数组的每次索引值的读取，就算做一步，也可以被称作为unit_time。

案例1：数组值获取（O（1））

获取数组第四个位置的值

  

 

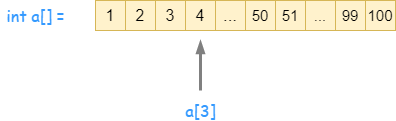
 如下代码：

int a[] = {0, 1, 2, 3, 4, 5, 6};
System.out.println(a[3]); // step1

  如上step1，获取a第三个位置的值，我们把这个时间称作为1步。实际上在计算机底层，计算机可以通过一步跳到任意一个索引的位置进行数据的读取，因此这个时间也被称为单位时间unit_time。

  如果用大O记法，我们称作为“常数时间--O（1）。用通俗的话解释也就是：无论数组的长度多少，获取数组中某个值的都只是1步。

  随着数组数量的增加，时间复杂度并不会提升。

如果用数学公式f(x)表示程序运行所需的时间（x表示数组的长度，后边坐标图都一样）

 

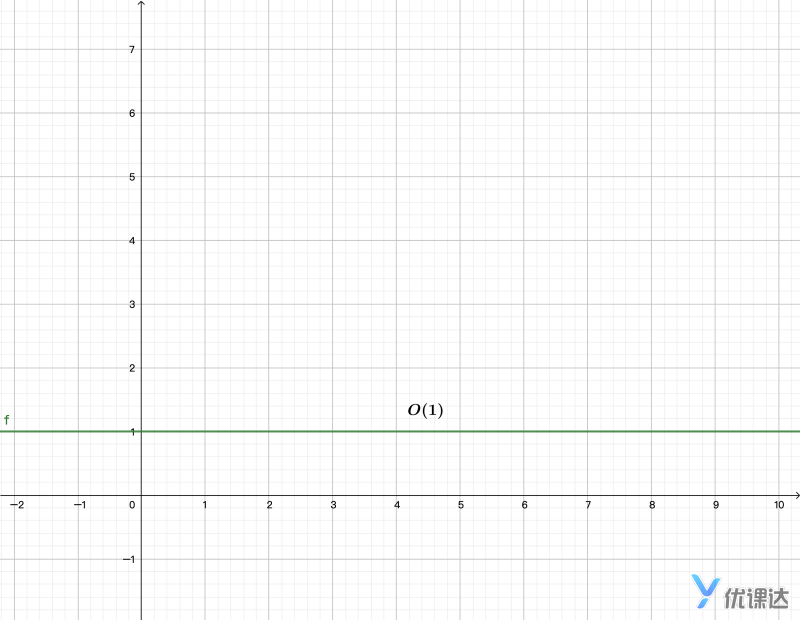
案例2：猜数字游戏（O（logN））

我们称为对数时间--O（logN)

用数学公式表示如下：

 

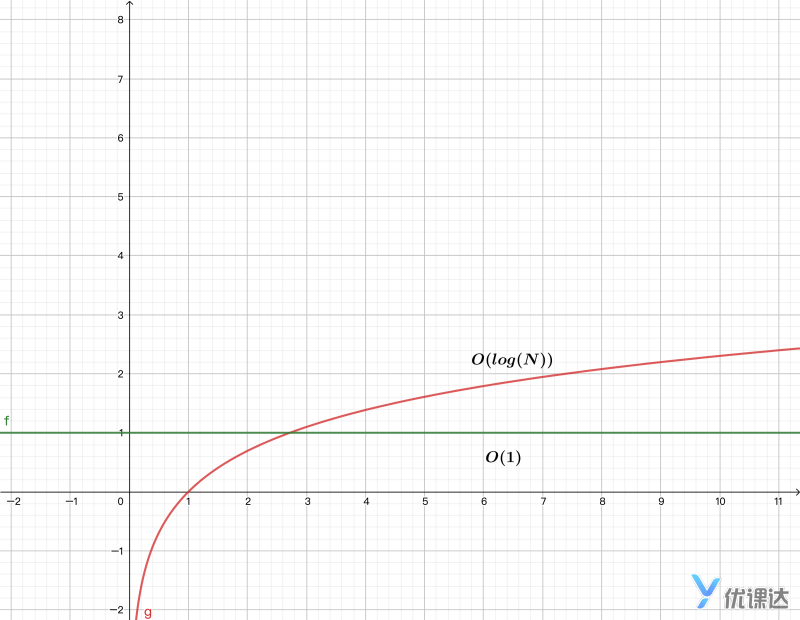
 可以看到O（logN)比O（1）增长的更快一些，性能更差一些。

 

案例3：计算N的阶乘O（N）

  

 

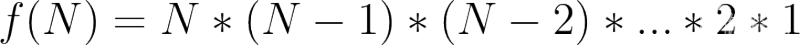
 代码如下：

public int factorial(int n) {
    int result = 1; //step1
    for (int i = 1; i <= n; i++) { //step2
        result *= i;  // step3
    }
    return result;
}

 

 在这种情况下，一共的时间复杂度为2N+2.

  如果用大O记法，我们称作为：线性时间O（2N+2）。

  忽略常量，常量，系数部分并不左右增长趋势，所以都可以忽略。所以上面O（2N+2），通常我们会表示为O（N）。

上面三个案例，用图示为：

 

 

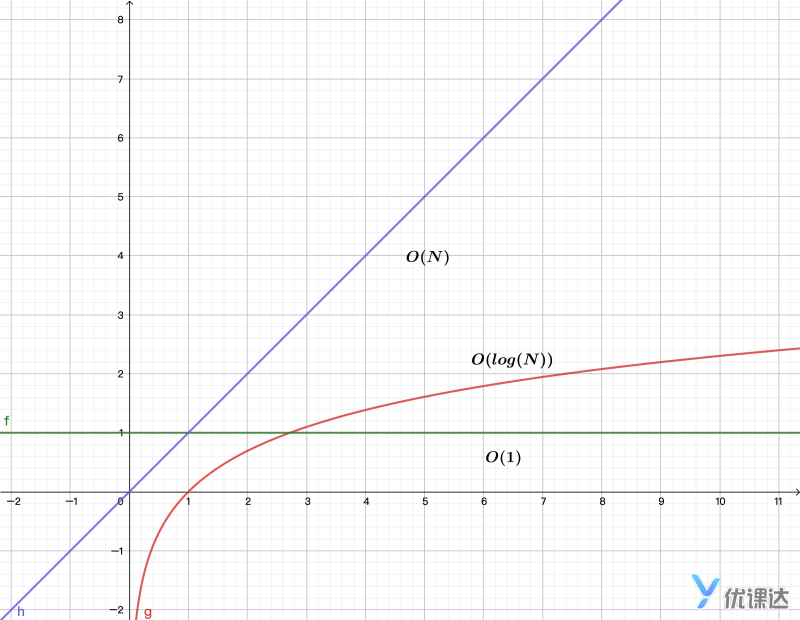
案例4：计算一个数组中的所有组合方式（O（N^2））

我们需要定义一个函数，能打印传入参数的两两组合情况。例如：我们传入一个数组{“hello","you","ke","da"},里面有4个英文词语，我们希望两两组合，那么一共有哪些组合情况呢？

 

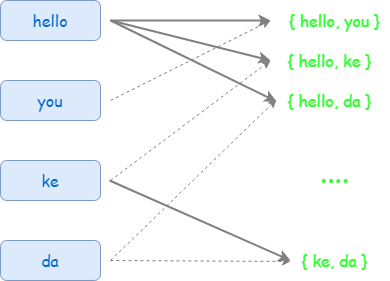
 代码如下：

public void combine(String args[]) {
    for (int i = 0; i < args.length; i++) { //step1
        for (int j = i + 1; j < args.length; j++) { //step2
            System.out.println(args[i] + args[j]); //step3
        }
    }
}

我们分析下下面的时间复杂度

 

 我们称作为指数时间--O（N^2).

把三个案例放在一起，我们看看时间复杂度的趋势

 

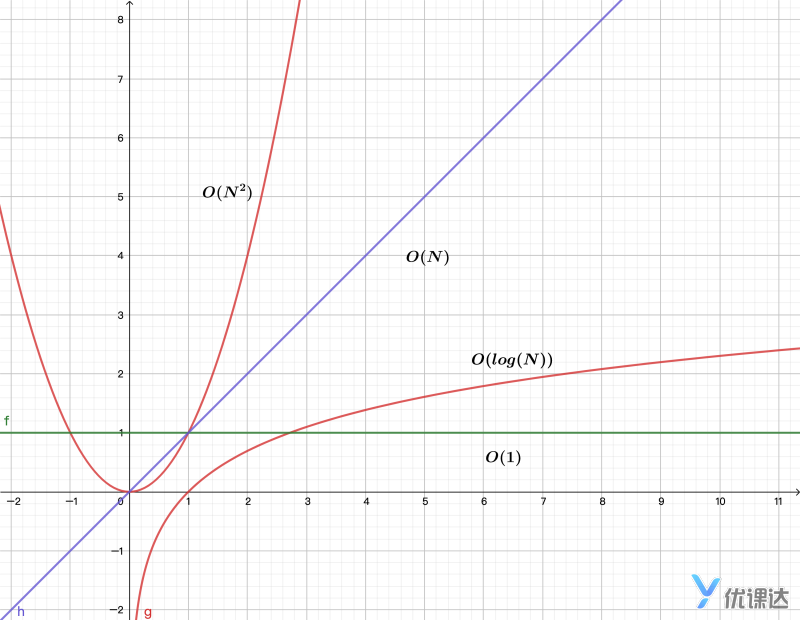
 大O记法，只保留最大趋势公式，指数>线性>对数>常数。

写代码时，如果能用线性复杂度的代码，替换指数复杂度的代码，那就是大大性能优化。

 

---

 

空间复杂度

空间复杂度是以一个基础数据类型值当做基础单位。

O（1）

int a = 0;
int j = 0;

O（N）

int a[] = new int[n]