快速模幂算法

快速模幂算法就是将指数变成二进制数来计算，每次按照底数的二进制次方进行计算，因为底数相乘指数相加，又模和乘可以相互变化，所以最后可以一边模一边乘，最后得出的结果还是正确的。

例如：$$10^4 mod 6可以转变为(10^2 * 10^2) mod 6,可以变化为(10^2 mod 6)* (10^2 mod 6),同样的操作最后就变为(10 mod 6)^4 mod 6(一边次方一边模)$$
人工计算思路如下：

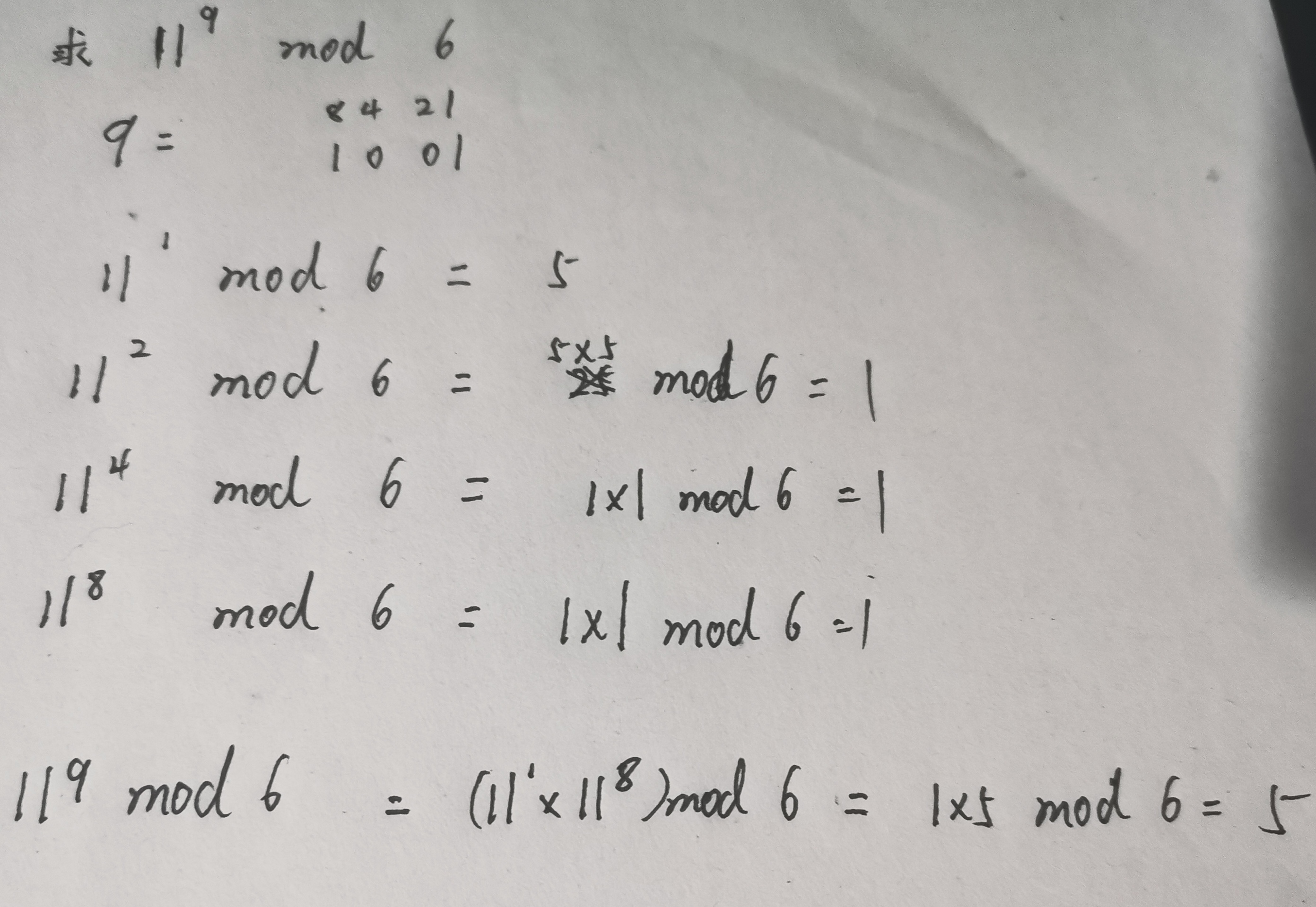
代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n, m, p;
int quick(LL a, LL b, LL c)
{
  if (b == 0) return 1;//0次方返回值为1
  LL A = 1;
  LL T = a % c;
  while (b != 0)
  {
    if (b & 1) A = (A * T) % c;
    b >>= 1;
    T = (T * T) % c;
  }
  return A;
}
int main()
{
  printf("请输入n的m次方模p，按顺序输入n, m, p:\n");
  cin >> n >> m >> p;
  cout << n << " ^ " << m << " mod " << p << " = " << quick(n, m, p);
}