Codeforces Round 450 D 隔板法+容斥

题意：

Count the number of distinct sequences a1, a2, ..., an (1 ≤ ai) consisting of positive integers such that gcd(a1, a2, ..., an) = xand 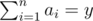. As this number could be large, print the answer modulo 109 + 7.

 

解法：

变成1+1+...+1=y/x ,用隔板法就知道有2^(y/x-1)个解

但是考虑到gcd不是1的情况。

 

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int mod=1e9+7;
ll quick_pow(ll a, ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
            ans=ans*a%mod;//ans*a%mod;
        a=a*a%mod;//a=a*a%mod;
        b>>=1;
    }
    return ans;
}

vector<int> v;
ll ans=0;
void dfs(int tot, int s, int len, int f){

    if(tot==v.size()){
        ans+=quick_pow(2, len/s-1)*f;
        ans=(ans+mod)%mod;
        return ;
    }

    dfs(tot+1, s*v[tot], len, -f);
    dfs(tot+1, s, len, f);
}

int main(){

    int x, y;
    scanf("%d%d", &x, &y);
    if(y%x==0){
        int len=y/x;
        for(int i=2 ;i*i<=len; i++){
            if(len%i==0){
                v.push_back(i);
                while(len%i==0){
                    len/=i;
                }
            }
        }
        if(len!=1){
            v.push_back(len);
        }
        //容斥
        dfs(0, 1, y/x, 1);
        printf("%lld\n", ans);
    }
    else{
        printf("0\n");
    }

    return 0;
}