AE（自动编码器）与VAE（变分自动编码器）简单理解

AE（Auto Encoder, 自动编码器）

AE的结构

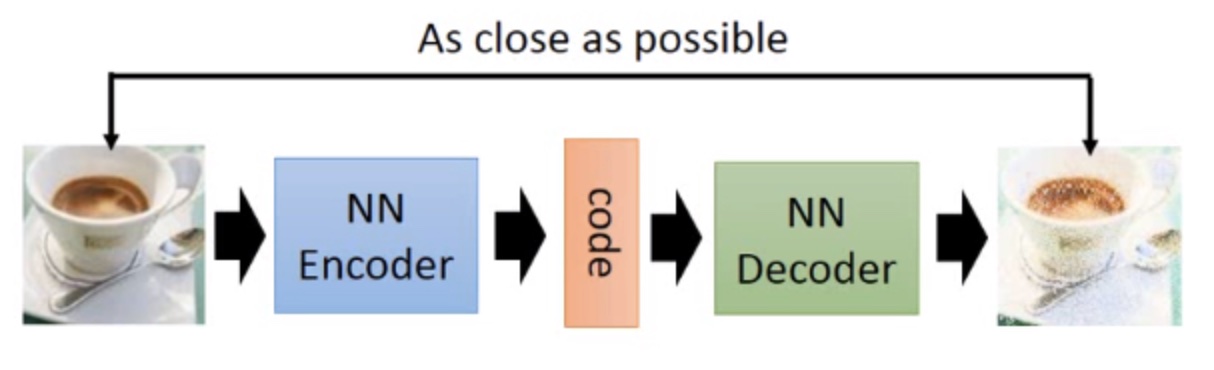
如上图所示，自动编码器主要由两部分组成：编码器（Encoder）和解码器（Decoder）。编码器和解码器可以看作是两个函数，一个用于将高维输入（如图片）映射为低维编码（code），另一个用于将低维编码（code）映射为高维输出（如生成的图片）。这两个函数可以是任意形式，但在深度学习中，我们用神经网络去学习这两个函数。

那如何去学呢？这里以图片为例，只需要输入一张图片（\(X\)），经过编码器（Encoder）网络，输出编码（code），再将编码（code）作为解码器网络（Decoder）的输入，输出一张新的图片（\(\hat X\)），最后最小化\(X\)与\(\hat X\)之间的差距（通常可用MSE误差）即可。

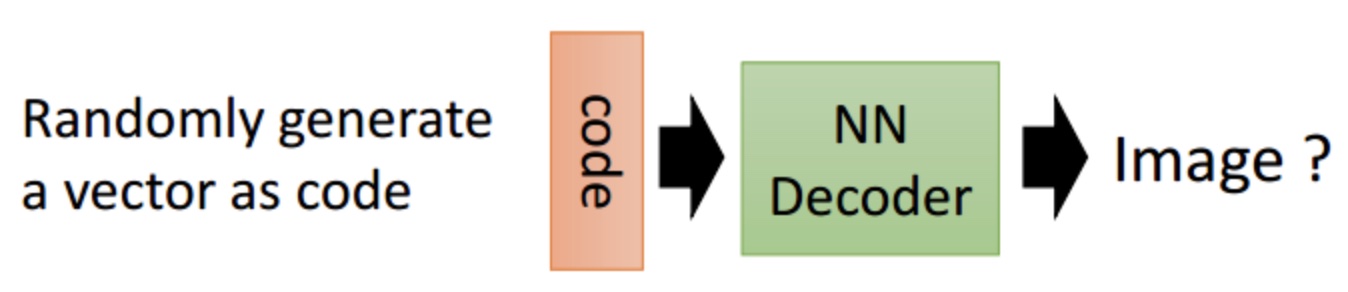
这时候我们直观想象只要拿出Decoder部分，随机生成一个code然后输入，就可以得到一张生成的图像。但实际上这样的生成效果并不好（下面解释原因），因此AE多用于数据压缩，而数据生成则使用下面所介绍的VAE更好。

AE的缺陷

由上面介绍可以看出，AE的Encoder是将图片映射成“数值编码”，Decoder是将“数值编码”映射成图片。这样存在的问题是，在训练过程中，随着不断降低输入图片与输出图片之间的误差，模型会过拟合，泛化性能不好。也就是说对于一个训练好的AE，输入某个图片，就只会将其编码为某个确定的code，输入某个确定的code就只会输出某个确定的图片，并且如果这个code来自于没见过的图片，那么生成的图片也不会好。下面举个例子来说明：

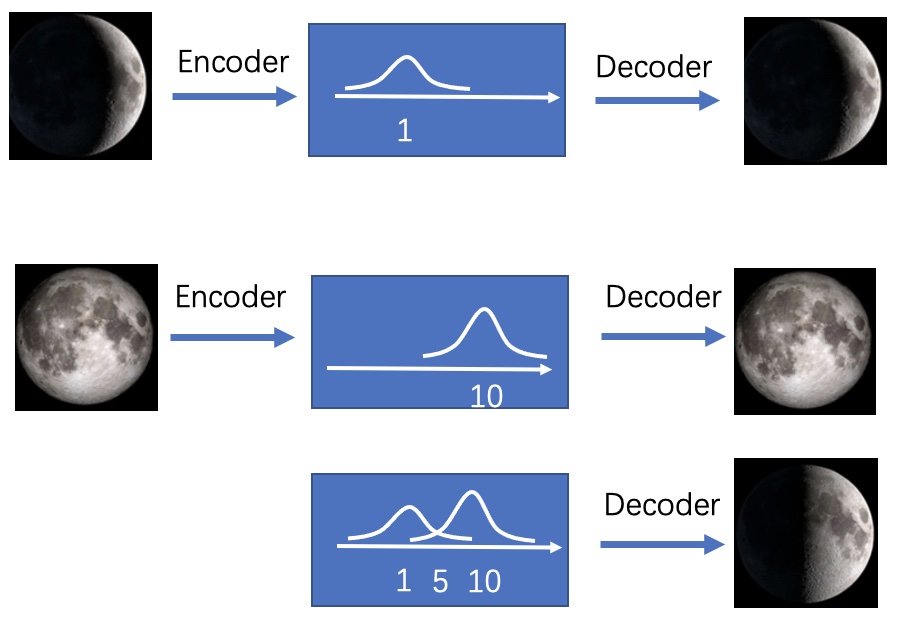
假设我们训练好的AE将“新月”图片encode成code=1（这里假设code只有1维），将其decode能得到“新月”的图片；将“满月”encode成code=10，同样将其decode能得到“满月”图片。这时候如果我们给AE一个code=5，我们希望是能得到“半月”的图片，但由于之前训练时并没有将“半月”的图片编码，或者将一张非月亮的图片编码为5，那么我们就不太可能得到“半月”的图片。因此AE多用于数据的压缩和恢复，用于数据生成时效果并不理想。

那如何解决以上问题呢？这时候我们转变思路，不将图片映射成“数值编码”，而将其映射成“分布”。还是刚刚的例子，我们将“新月”图片映射成\(\mu=1\)的正态分布，那么就相当于在1附近加了噪声，此时不仅1表示“新月”，1附近的数值也表示“新月”，只是1的时候最像“新月”。将"满月"映射成\(\mu=10\)的正态分布，10的附近也都表示“满月”。那么code=5时，就同时拥有了“新月”和“满月”的特点，那么这时候decode出来的大概率就是“半月”了。这就是VAE的思想。

VAE（Variational Auto-Encoder, 变分自动编码器）

VAE的结构

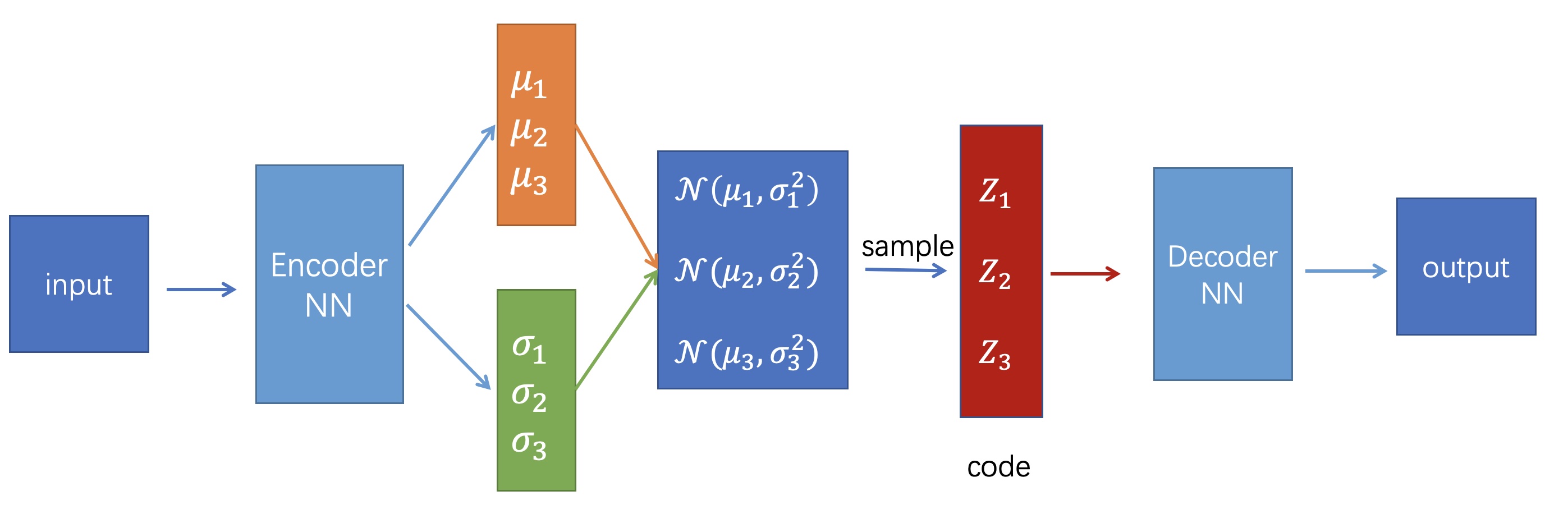
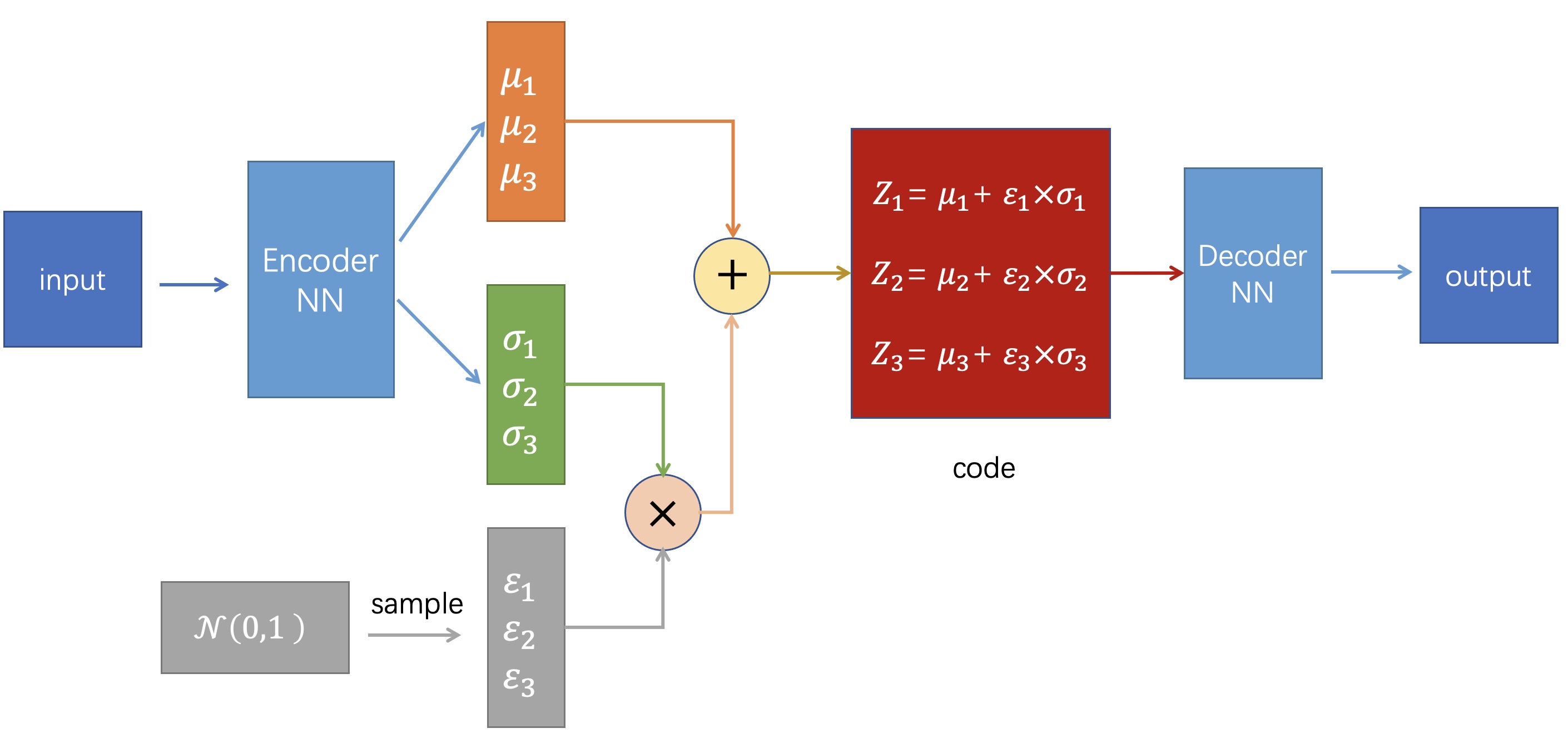
如上图所示，VAE与AE整体结构类似，不同的地方在于AE的Encoder直接输出code，而VAE的Encoder输出的是若干个正态分布的均值(\(\mu_1,\mu_2...\mu_n\))和标准差(\(\sigma_1,\sigma_2...\sigma_n\))，然后从每个正态分布\(\mathcal{N}\left(\mu_{1}, \sigma_{1}^2\right),\mathcal{N}\left(\mu_{2}, \sigma_{2}^2\right)...\mathcal{N}\left(\mu_{n}, \sigma_{n}^2\right)\)采样得到编码code\((Z_1,Z_2...Z_n)\)，再将code送入Decoder进行解码。

那如何进行训练呢？在训练过程中，VAE的Loss函数由两部分组成：

为了让输出和输入尽可能像，所以要让输出和输入的差距尽可能小，此部分用MSELoss来计算，即最小化MSELoss。
训练过程中，如果仅仅使输入和输出的误差尽可能小，那么随着不断训练，会使得\(\sigma\)趋近于0，这样就使得VAE越来越像AE，对数据产生了过拟合，编码的噪声也会消失，导致无法生成未见过的数据。因此为了解决这个问题，我们要对\(\mu\)和\(\sigma\)加以约束，使其构成的正态分布尽可能像标准正态分布，具体做法是计算\(\mathcal{N}\left(\mu_{}, \sigma_{}^2\right)\)与\(\mathcal{N}\left(0, 1\right)\)之间的KL散度，即最小化下式（具体推导过程下面介绍）：

\[\mathrm {KL}(\mathcal{N}\left(\mu_{}, \sigma_{}^2\right)||\mathcal{N}\left(0, 1\right))=\frac{1}{2}\left(-\log \sigma^{2}+\mu^{2}+\sigma^{2}-1\right) \]

但是我们注意到这里的code是通过从正态分布中采样得到的，这个采样的操作是不可导的，这会导致在反向传播时\(Z\)对\(\mu\)和\(\sigma\)无法直接求导，因此这里用到一个trick：重参数化技巧（reparametrize）。具体思想是：从\(\mathcal{N}\left(0, 1\right)\)中采样一个\(\varepsilon\)，然后让\(Z=\mu+\varepsilon\times\sigma\)，这就相当于直接从\(\mathcal{N}\left(\mu_{}, \sigma_{}^2\right)\)中采样\(Z\)。具体过程如下所示：

KL Loss推导

先导知识

连续随机变量下KL散度公式：

\[\mathrm{KL}(P \| Q)=\int P(x) \log \frac{P(x)}{Q(x)} d x \]

连续随机变量下期望公式：

设连续型随机变量\(X\)的概率密度函数为\(f(x)\)，且积分绝对收敛，则期望为：

\[E(X)=\int_{-\infty}^{\infty} x f(x) d x \]

若随机变量\(Y\)符合\(Y=g(X)\)，\(X\)的概率密度函数为\(f(x)\)，且\(g(x)f(x)\)的积分绝对收敛，则期望为：

\[E(Y)=E(g(X))=\int_{-\infty}^{\infty} g(x) f(x) d x \]

方差公式：

\[\mathrm D(\mathrm X) = \mathrm E\big([x-\mathrm E(\mathrm X)]^2\big)= \mathrm E(\mathrm X^2)-[\mathrm E(\mathrm X)]^2 \]

正态分布公式：

\(X \sim N\left(\mu, \sigma^{2}\right)\)的概率密度函数：

\[f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \]

KL Loss推导过程

\[\begin{aligned} \mathrm {KL}(\mathcal{N}\left(\mu_{}, \sigma_{}^2\right)||\mathcal{N}\left(0, 1\right)) &=\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\left(\log \frac{\exp\big({-(x-\mu)^{2} / 2 \sigma^{2}\big) \big/ \sqrt{2 \pi \sigma^{2}}}}{\exp\big({-x^{2} / 2\big) \big/ \sqrt{2 \pi}}}\right)\ dx\\ &=\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\log \bigg( \frac{1}{\sqrt{\sigma^2}}\cdot \exp\big(\frac 1 2(x^2-(x-\mu)^2/\sigma^2)\big) \bigg)\ d x\\ &=-\frac 1 2 \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\bigg(\log\sigma^2-x^2+(x-\mu)^2/\sigma^2\bigg)\ dx \end{aligned} \]

其中展开可以分为三项：

第一项：

\[\begin{aligned} &\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\cdot \log\sigma^2 \ dx\\ &=\log\sigma^2\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg) \ dx\\ &=\log\sigma^2 \end{aligned} \]

此处注意：概率密度函数的积分为1

第二项：

\[\begin{aligned} &\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\cdot x^2 \ dx\\ \end{aligned} \]

这里的化简技巧是：根据\(E(Y)=E(g(X))=\int_{-\infty}^{\infty} g(x) f(x) d x\)，将上式中\(\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\)看作\(f(x)\)，将\(x^2\)看作\(g(x)\)，则有：

\[\begin{aligned} \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\cdot x^2 \ dx &=\mathrm E(\mathrm X^2) \\ &=\mathrm D(\mathrm X)+[\mathrm E(\mathrm X)]^2\\ &=\sigma^2+\mu^2 \end{aligned} \]

其中\(X \sim N\left(\mu, \sigma^{2}\right)\)

第三项：

\[\begin{aligned} &\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\cdot (x-\mu)^2/\sigma^2 \ dx\\ &=\frac {1} {\sigma^2} \int \frac{(x-\mu)^2}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\ dx\\ \end{aligned} \]

这里的化简技巧同上面第二项的化简类似，将上式中\(\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\)看作\(f(x)\)，将\((x-\mu)^2=\big(x-\mathrm E(\mathrm X)\big)^2\)看作\(g(x)\)，则有：

\[\begin{aligned} \frac {1} {\sigma^2} \int \frac{(x-\mu)^2}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\ dx &=\frac {1} {\sigma^2} \cdot \mathrm E\big([x-\mathrm E(\mathrm X)]^2\big)\\ &=\frac {1} {\sigma^2} \cdot \mathrm D(\mathrm X) \\ &= \frac {1} {\sigma^2} \cdot \sigma^2\\ &=1 \end{aligned} \]

综上所述：

\[\begin{aligned} \mathrm {KL}(\mathcal{N}\left(\mu_{}, \sigma_{}^2\right)||\mathcal{N}\left(0, 1\right)) &=-\frac 1 2 \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\bigg({-(x-\mu)^{2} / 2 \sigma^{2}}\bigg)\bigg(\log\sigma^2-x^2+(x-\mu)^2/\sigma^2\bigg)\ dx\\ &=-\frac 1 2(\log\sigma^2-\sigma^2-\mu^2+1) \end{aligned} \]