64. 最小路径和

64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

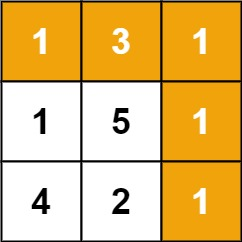
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

动态规划

• 本题的dp数组含义比较容易确定，即\(dp[i][j]\)表示从起点到\((i,j)\)终点的最短距离。
• 更新公式类似，因为只能向下或者向右走，因此\(dp[i][j]\)由\(dp[i-1][j]\)和\(dp[i][j-1]\)中的较小值决定；
• 边界条件是第一行与第一列，特殊处理。
• 最后需要根据更新方程，检查一下如何遍历数组，\(dp[i-1][j]\)和\(dp[i][j-1]\)需要在\(dp[i][j]\)更新之前遍历过，因此有，\(i\)从前向后遍历是外层循环，\(j\)从前往后遍历是内层循环。

 int minPathSum(vector<vector<int>>& grid) {
        // 向下或向右行走
        // 动态规划
        // dp[i][j]: 表示从起点到dp[i][j]的最短路径
        
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));

        // 边界条件
        dp[0][0] = grid[0][0];
        for(int i = 1; i < m; ++i){
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for(int j = 1; j < n; ++j){
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }

        // 更新方程
        for(int i = 1; i < m; ++i){
            for(int j = 1; j < n; ++j){
                dp[i][j] = min(dp[i-1][j]+grid[i][j], dp[i][j-1]+grid[i][j]);
            }
        }

        return dp[m-1][n-1];
    }

DFS

• 本题也可以使用深度优先搜索，寻找最短路径，因此需要存储一个指针地址，代表当前的最短路径，需要一个int输入，代表当前的路径和。
• 最短路径到终点\((m-1, n-1)\)才更新，终止条件写作寻常的越界即可。
• dfs递归调用，向右一格或向下一格，比较简单。
• 提前剪枝，如果当前的路径和sum大于最短路径ans，提前return，不需要再到终点了。
• 未通过最后一个测试例子

class Solution {
private:
    void dfs(int& ans, vector<vector<int>>& grid, int l, int r, int sum){
        int m = grid.size(), n = grid[0].size();
        if(l >= m || r >= n)
            return;
        // 更新路径和
        sum += grid[l][r];
        // 提前剪枝
        if(sum >= ans)
            return;
        // 更新最短路径
        if(l == m-1 && r == n-1)
            ans = min(sum, ans);
        // dfs
        dfs(ans, grid, l+1, r, sum);
        dfs(ans, grid, l, r+1, sum);
    }
public:
    int minPathSum(vector<vector<int>>& grid) {
        // dfs
        int m = grid.size(), n = grid[0].size();
        int ans = INT_MAX;
        dfs(ans, grid, 0, 0, 0);
        return ans;   
    }
};