最小乘积模型

P5540 [BalkanOI 2011] timeismoney

最小乘积模型的模板。

给定一个图，每条边有两种边权 \(a,b\)，要求最小化图的一棵生成树的：

\[(\sum a_i)\times (\sum b_i) \]

基础的想法是这个东西的限制是二维的。由于这个是乘积的形式，那么我们可以令 \(x=\sum a,y=\sum b\)，将其放到二维平面上去做。

这样当这个乘积固定的时候，那么可能的答案的点就在 \(k=\) 这个乘积的反比例函数上。由于反比例函数是下凸壳的形式，我们又要求这个东西的最小值，因此可能成为答案的点也形成一个下凸壳。

整个图可能形成的生成树个数可以达到 \(n!\) 级别。如果我们只考虑凸壳上的点显然可以提升效率。考虑如何找到凸壳上的点。
首先我们可以简单地划定这个凸壳的最左端的点与最右端的点，即只考虑 \(a\) 的最小生成树以及只考虑 \(b\) 的最小生成树。然后分别求出对应坐标。假设这两个点分别为 \(A,B\)。可以发现这个是简单的。

然后考虑凸壳剩下的部分只有可能在这两个点分别向 \(x\) 轴与 \(y\) 轴围成的三角形内。因此我们可以通过去找到离 \(A,B\) 两个点最远的点 \(C\)，然后分治 \(A,C\) 与 \(C,B\) 的部分。需要注意的是这个分治不代表任何东西。要找到“最远的 \(C\)”仅仅是为了保证 \(C\) 在这个凸壳上。这个东西实际上就是在枚举凸壳上的所有点。要分治的原因是我们可以通过 某种方法 在知道两个凸壳上的点的情况下找到某个凸壳上在它们之间的点而已。

现在我们就来介绍一下这个 某种方法。
可以发现，如果要找到一个点 \(C\) 最远，一个有效的方式是使得 \(A,B,C\) 三个点围成的三角形面积最大。这样找出来的点 \(C\) 就一定在凸壳上了。根据上面的分析，由于我们只需要保证这一个条件，不需要保证复杂度之类的，因此满足这个条件就够了。

考虑这个东西怎么求。先盗个图。@xgzc。

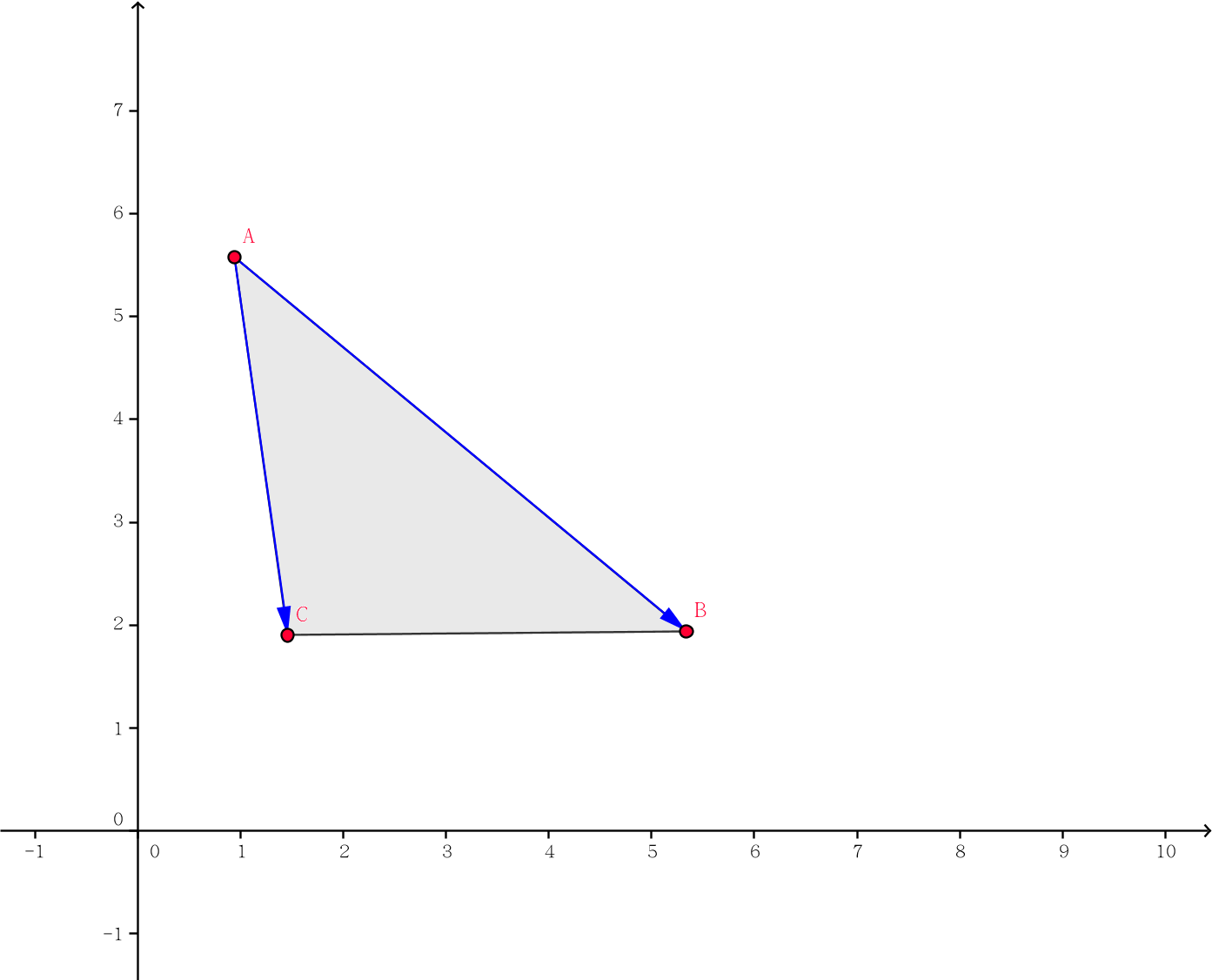
可以发现实际上就是最小化 $\overrightarrow{AB} \times \overrightarrow{AC} $。（因为这个意义下叉积一定是负数，实际上就是最大化面积）

然后可以将其拆开成式子。

\[\begin{aligned} \overrightarrow{AB} \times \overrightarrow{AC} &= (x_B - x_A)(y_C - y_A) - (y_B - y_A)(x_C - x_A) \\ &= (y_A - y_B)x_C + (x_B - x_A)y_C - x_B y_A + y_B x_A \end{aligned} \]

可以发现最后两项是定值。于是目标就是最小化前两项。由于前两项的系数也是常数，因此我们可以直接将图的边权设为 \((y_A - y_B)a_i + (x_B - x_A)b_i\)。
然后直接暴力跑最小生成树即可。可以发现这个时候跑 prim 更快。

复杂度分析是困难的。由于我们实际上枚举了凸壳上的所有点，因此复杂度阈值就是凸壳上的点数与最小生成树复杂度的乘积。
可以通过相对难以理解的东西证明凸包上的点数是 \(R^{\frac{2}{3}}\) 的，其中 \(R\) 是横坐标的值域。
或者也有一个证明凸包上的点的期望是 \(\sqrt {\ln n!}\) 的。看不懂，太困难了。（事实上这种所谓的期望证明只是期望，并不能代表真正的复杂度，因此复杂度阈值还是上面 \(R^{\frac{2}{3}}\) 比较严谨）

code

写的 prim。注意细节，比如编号从 0 开始（因为这个东西调了一个半小时）。（略有压行？）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pii pair <int,int>
#define mp make_pair
const int N=205,inf=6e4+7;
int n,m,a[N][N],b[N][N],vis[N];
ll dis[N],disa[N],disb[N];
pii ans;
ll get(int xa,int ya,int xb,int yb,int ai,int bi){return 1ll*(xb-xa)*bi+1ll*(ya-yb)*ai;} //求距离
pii prim(int xa,int ya,int xb,int yb){
    for(int i=1;i<=n;i++)dis[i]=min(1ll*inf*inf,get(xa,ya,xb,yb,a[1][i],b[1][i])),vis[i]=0,disa[i]=a[1][i],disb[i]=b[1][i];
    int u=1,ansa=0,ansb=0,num=0,tmpa=0,tmpb=0;dis[1]=0;ll val=inf*inf;
    while(num<n-1){
        num++;vis[u]=1;val=1ll*inf*inf;
        for(int i=1;i<=n;i++)if(!vis[i]&&dis[i]<val)u=i,val=dis[i],tmpa=disa[i],tmpb=disb[i];
        ansa+=tmpa,ansb+=tmpb;
        for(int i=1;i<=n;i++)if(!vis[i]&&dis[i]>get(xa,ya,xb,yb,a[u][i],b[u][i]))dis[i]=get(xa,ya,xb,yb,a[u][i],b[u][i]),disa[i]=a[u][i],disb[i]=b[u][i];
    }
    return mp(ansa,ansb);
}
void solve(int xa,int ya,int xb,int yb){
    if(xa*yb>=ans.first*ans.second||(xa==xb&&ya==yb))return;   //小优化，如果当前区间最小的可能答案已经不优了就跳
    pii tmp=prim(xa,ya,xb,yb);int xc=tmp.first,yc=tmp.second;
    if(1ll*xc*yc<1ll*ans.first*ans.second||((1ll*xc*yc==1ll*ans.first*ans.second)&&xc<ans.first))ans=tmp;
    if(1ll*(xb-xa)*(yc-ya)-1ll*(xc-xa)*(yb-ya)>=0)return;
    solve(xa,ya,xc,yc),solve(xc,yc,xb,yb);
}
signed main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)a[i][j]=b[i][j]=inf;
    for(int k=1,u,v,wa,wb;k<=m;k++)cin>>u>>v>>wa>>wb,u++,v++,a[u][v]=a[v][u]=wa,b[u][v]=b[v][u]=wb;
    pii tmp=prim(0,1,0,0);int xa=tmp.first,ya=tmp.second;
    tmp=prim(0,0,1,0);int xb=tmp.first,yb=tmp.second;
    ans=mp(inf,inf);if(xa*ya<xb*yb)ans=mp(xa,ya);else ans=mp(xb,yb);
    solve(xa,ya,xb,yb);
    cout<<ans.first<<' '<<ans.second;return 0;
}