数据结构之树（二叉运算树）

什么是二叉运算树

二叉运算树（Binary Expression Tree），也称为二叉表达式树，是一种数据结构，用于求解数学表达式或算术表达式。它是一种二叉树，其中每个节点表示一个操作符或操作数，并且具有以下特点：

1. 叶子节点（没有子节点）表示操作数，如整数或变量。
2. 内部节点表示操作符，如加法、减法、乘法、除法等。
3. 树的根节点表示整个表达式的最外层操作符。
4. 每个内部节点的左子节点和右子节点分别表示操作符的操作数或子表达式。

二叉运算树使我们能够以树状结构的方式组织和表示数学表达式，可以轻松进行表达式求值。通过遍历这棵树，可以按照正确的操作符优先级和结合性计算表达式的值。

例如，对于表达式 "3 + 4 * 2"，可以构建如下的二叉运算树：

 

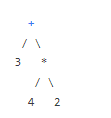
这个树的根节点是加法操作符，左子节点是操作数 3，右子节点是乘法操作符。乘法操作符的左子节点是操作数 4，右子节点是操作数 2。通过遍历这棵树，可以按照正确的顺序执行操作，计算表达式的值。

二叉运算树用于编译器、解释器和数学表达式求解中，它提供了一种有效的方式来表示和处理复杂的数学表达式。

 

Python代码示例

 

 

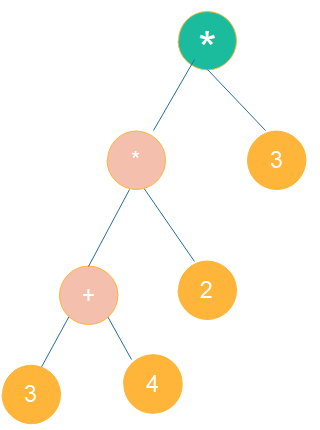
# 步骤1：定义操作数和操作符的优先级
operator_precedence = {
    '+': 1,
    '-': 1,
    '*': 2,
    '/': 2,
    '^': 3  # 假设有指数运算
}


# 步骤2: 创建节点类
class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None


# 步骤3: 解析表达式并构建二叉运算树
def build_expression_tree(expression):
    stack = []
    operator_stack = []
    tokens = expression.split()

    for token in tokens:
        if token == '(':
            operator_stack.append(token)
        elif token == ')':
            while operator_stack and operator_stack[-1] != '(':
                operator = operator_stack.pop()
                right = stack.pop()
                left = stack.pop()
                node = TreeNode(operator)
                node.left = left
                node.right = right
                stack.append(node)
            operator_stack.pop()  # 弹出左括号
        elif token.isnumeric():
            node = TreeNode(token)
            stack.append(node)
        elif token in operator_precedence:
            while (operator_stack and operator_stack[-1] != '(' and
                   operator_precedence[token] <= operator_precedence.get(operator_stack[-1], 0)):
                operator = operator_stack.pop()
                right = stack.pop()
                left = stack.pop()
                node = TreeNode(operator)
                node.left = left
                node.right = right
                stack.append(node)
            operator_stack.append(token)

    while operator_stack:
        operator = operator_stack.pop()
        right = stack.pop()
        left = stack.pop()
        node = TreeNode(operator)
        node.left = left
        node.right = right
        stack.append(node)

    return stack[0]


# expression = "( 3 + 4 ) * 2 ^ ( 2 - 1 )"     # 14
expression = "( 3 + 4 ) * 2 * 3"
root_tree = build_expression_tree(expression)


# 打印二叉运算树
def print_tree(node):
    if node:
        print(node.value)
        print_tree(node.left)
        print_tree(node.right)


print_tree(root_tree)


# 使用二叉运算树计算表达式
def evaluate_expression_tree(root):
    if root is None:
        return 0

    if root.left is None and root.right is None:
        return int(root.value)

    left_result = evaluate_expression_tree(root.left)
    right_result = evaluate_expression_tree(root.right)

    # AttributeError: 'int' object has no attribute 'isnumeric'
    # if root.value == '+' and left_result.isnumeric() and right_result.isnumeric():
    if root.value == '+' and isinstance(left_result, int) and isinstance(right_result, int):
        return left_result + right_result
    elif root.value == '-' and isinstance(left_result, int) and isinstance(right_result, int):
        return left_result - right_result
    elif root.value == '*' and isinstance(left_result, int) and isinstance(right_result, int):
        return left_result * right_result
    elif root.value == '/' and isinstance(left_result, int) and isinstance(right_result, int):
        return left_result / right_result
    elif root.value == '^' and isinstance(left_result, int) and isinstance(right_result, int):
        return left_result ** right_result


print(evaluate_expression_tree(root_tree))

输出：

*
*
+
3
4
2
3
42

　　

Java代码示例

1. 树节点

/**
 * 树节点
 */
public class TreeNode {
    /**
     * 该节点的值
     */
    String value;
    /**
     * 左子节点
     */
    TreeNode left;
    /**
     * 右子节点
     */
    TreeNode right;

    public TreeNode(String value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }

    @Override
    public String toString() {
        return "TreeNode{" +
                "value='" + value + '\'' +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
}

2. 二叉运算树

用于把表达式转换为二叉运算树，以后用于计算表达式。

import java.util.HashMap;
import java.util.Map;
import java.util.Stack;

/**
 * 二叉运算树
 */
public class ExpressionTree {

    public static final Map<String, Integer> WEIGHT_MAP = new HashMap<String, Integer>();

    static {
        WEIGHT_MAP.put("+", 1);
        WEIGHT_MAP.put("-", 1);
        WEIGHT_MAP.put("*", 2);
        WEIGHT_MAP.put("/", 2);
    }


    private Stack<String> operatorStack = new Stack<>();
    private Stack<TreeNode> stack = new Stack<>();

    /**
     * 根据表达式构造运算二叉树
     *
     * @param expression
     * @return
     */
    public TreeNode buildExpressionTree(String expression) {
        if (expression == null || expression.isEmpty()) {
            return null;
        }
        expression = addSpacesToExpression(expression);
        String[] tokens = expression.split(" ");
        // 不能使用for-each保证其顺序
        for (int i = 0; i < tokens.length; i++) {
            String token = tokens[i];
            if (token == "(") {
                operatorStack.add(token);
            } else if (token == ")") {
                while (!operatorStack.isEmpty() && !operatorStack.peek().equals("(")) {
                    String operator = operatorStack.pop();
                    TreeNode right = stack.pop();
                    TreeNode left = stack.pop();
                    TreeNode treeNode = new TreeNode(operator);
                    treeNode.left = left;
                    treeNode.right = right;
                    stack.add(treeNode);
                }
                operatorStack.pop(); // 弹出左括号
            } else if (isNumeric(token)) {
                TreeNode treeNode = new TreeNode(token);
                stack.add(treeNode);
            } else if (WEIGHT_MAP.containsKey(token)) {
                while (!operatorStack.isEmpty() && !operatorStack.peek().equals("(") && WEIGHT_MAP.get(token) <= WEIGHT_MAP.getOrDefault(operatorStack.peek(), 0)) {
                    String operator = operatorStack.pop();
                    TreeNode right = stack.pop();
                    TreeNode left = stack.pop();
                    TreeNode treeNode = new TreeNode(operator);
                    treeNode.right = right;
                    treeNode.left = left;
                    stack.add(treeNode);
                }
                operatorStack.add(token);
            }

        }
        while (!operatorStack.isEmpty()) {
            String operator = operatorStack.pop();
            TreeNode right = stack.pop();
            TreeNode left = stack.pop();
            TreeNode treeNode = new TreeNode(operator);
            treeNode.left = left;
            treeNode.right = right;
            stack.add(treeNode);

        }
        return stack.get(0);

    }

    /**
     * 判断是否是数字型字符串
     *
     * @param str
     * @return
     */
    public boolean isNumeric(String str) {
        return str.matches("-?\\d+(\\.\\d+)?");  // 匹配整数和浮点数，包括负数
    }

    /**
     * 数字、加减乘除前后添加空格
     *
     * @param expression
     * @return
     */
    public String addSpacesToExpression(String expression) {
        // 在数字、运算符前后加空格
        String result = expression.replaceAll("(\\d)([+\\-*/()])", "$1 $2").replaceAll("([+\\-*/()])(\\d)", "$1 $2");

        return result;
    }
}

3. 运算表达式

/**
 * 二叉运算树表达式计算
 */
public class ExpressionCalculator {
    /**
     * 计算二叉运算树表示的运算表达式的值，此方法只支持加减乘除
     *
     * @param root 树的根节点
     * @return 二叉运算树运算结果
     */
    public int evaluateExpression(TreeNode root) {
        if (root == null) {
            return 0;
        }


        if (isNumeric(root.value) && root.right == null && root.left == null) {
            return Integer.parseInt(root.value);
        }

        int leftValue = evaluateExpression(root.left);
        int rightValue = evaluateExpression(root.right);
//        System.out.println("leftValue:" + leftValue);
//        System.out.println("rightValue:" + rightValue);
        switch (root.value) {
            case "+":
                return leftValue + rightValue;
            case "-":
                return leftValue - rightValue;
            case "*":
                return leftValue * rightValue;
            case "/":
                return leftValue / rightValue;
            default:
                throw new IllegalArgumentException("Invalid operator: " + root.value);
        }
    }

    public boolean isNumeric(String str) {
        return str.matches("-?\\d+(\\.\\d+)?");  // 匹配整数和浮点数，包括负数
    }

}

4. 测试类

 

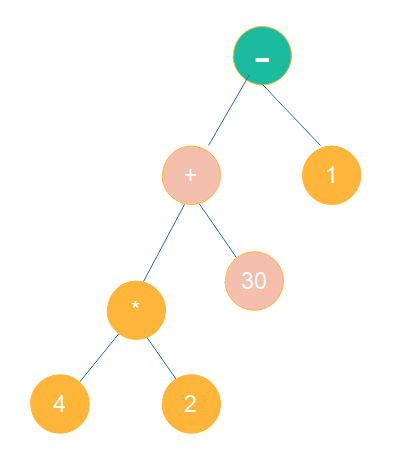
public class Main {
    public static void main(String[] args) {// 1. 表达式
        String expression = "(30 + (4 * 2)) - 1";
        // 2. 构造二叉运算树，并获取其根节点
        ExpressionTree expressionTree = new ExpressionTree();
        TreeNode root = expressionTree.buildExpressionTree(expression);
        printTree(root);
        // 3. 计算表达式的值
        ExpressionCalculator calculator = new ExpressionCalculator();
        int result = calculator.evaluateExpression(root);

        System.out.println("表达式 " + expression + " 的计算结果为 " + result);
    }

    public static void printTree(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.println(root.value);
        printTree(root.left);
        printTree(root.right);
    }
}

输出结果：

-
+
30
*
4
2
1
表达式 (30 + (4 * 2)) - 1 的计算结果为 37