数据结构之树（二叉树的存储方式之链表）

合集 - 数据结构与算法(24)
1.算法衡量优劣之时间复杂度2.数据结构与算法之概念3.算法衡量优劣之空间复杂度4.数据结构之数组5.数据结构之链表6.数据结构之栈7.N-皇后问题8.算术表达式的表示法（即求值法）9.算术表达式求值法（表达式求值）之前序表示法求值10.算术表达式求值法（表达式求值）之后序表示法求值11.数据结构之队列（一般队列）12.数据结构之队列（循环队列）13.数据结构之队列（双向队列）14.数据结构之树（基本概念）15.数据结构之树（二叉树）16.数据结构之树（Huffman tree(赫夫曼树 / 霍夫曼树 / 哈夫曼树 / 最优二叉树)）17.数据结构之树（二叉树的存储方式之数组）
18.数据结构之树（二叉树的存储方式之链表）
19.数据结构之树（遍历）20.数据结构之树（二叉运算树）21.数据结构之树（二叉搜索树）22.数据结构之树（线索树）23.数据结构之树（树转化为二叉树也叫二叉化）24.确定唯一二叉树
收起

Java

Java中可以使用链表来实现二叉树的存储。

1. 链表实现二叉树的原理：

   链表是由节点组成的数据结构，每个节点包含一个数据和指向下一个节点的指针。

   在链表中，可以将二叉树的每个节点都看作一个链表节点，同时维护一个指向左子节点的指针和一个指向右子节点的指针。通过这种方式，可以将二叉树的各个节点进行连接，从而实现二叉树的存储。

2. 最佳实践：

   在链表中实现二叉树时，可以定义一个二叉树节点类，该类包含一个数据字段和两个指针字段，分别用于连接左子节点和右子节点。同时，还需要定义一个链表类，该类包含一个指向根节点的指针字段，用于表示二叉树的起始位置。

示例

节点类：表示树的节点

复制代码
 1 public class TreeNode {
 2     // 数据
 3     int data;
 4     // 左子节点
 5     TreeNode left;
 6     // 右子节点
 7     TreeNode right;
 8     public TreeNode(int data) {
 9         this.data = data;
10         this.left = null;
11         this.right = null;
12     }
13 }
复制代码

二叉树类：表示树对象

复制代码
 1 import java.util.LinkedList;
 2 import java.util.Queue;
 3 
 4 /**
 5  * 树类即一个BinaryTree对象代表一个树
 6  */
 7 public class BinaryTree {
 8 
 9     TreeNode root;
10     public BinaryTree(int data) {
11         this.root = new TreeNode(data);
12     }
13     public void insert(int data) {
14         TreeNode newNode = new TreeNode(data);
15         if (root == null) {
16             root = newNode;
17             return;
18         }
19         // 每次都需要遍历，塑造树
20         // 0. 创建树对象
21         Queue<TreeNode> queue = new LinkedList<>();
22         // 1. 根入链
23         queue.offer(root);
24         // 2. 遍历 : 塑造树
25         while (!queue.isEmpty()) {
26             // 2.1 遍历所有节点，判断左右子节点是否为空，顺序先左后右
27             TreeNode current = queue.poll();
28             // 2.2 左子节点为空，当前插入节点作为其左节点
29             if (current.left == null) {
30                 current.left = newNode;
31                 return;
32             } else {
33                 // 2.2 左子节点不为空，入链塑造树
34                 queue.offer(current.left);
35             }
36             // 2.3 遍历所有节点，判断右子节点是否为空
37             //  为空，当前插入节点作为其右子节点
38             if (current.right == null) {
39                 current.right = newNode;
40                 return;
41             } else {
42                 // 不为空，入链，塑造树
43                 queue.offer(current.right);
44             }
45         }
46     }
47 }
复制代码

测试类

 

public class Main {
    public static void main(String[] args) {
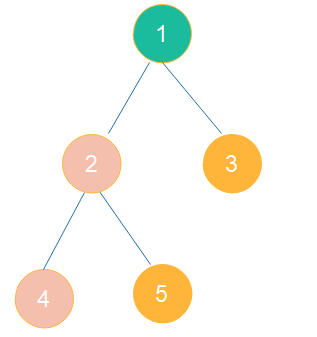
        BinaryTree binaryTree = new BinaryTree(1);
        binaryTree.insert(2);
        binaryTree.insert(3);
        binaryTree.insert(4);
        binaryTree.insert(5);
        System.out.println("Binary Tree traversal:");
        traversalBinaryTree(binaryTree.root);
    }
//    遍历树： 前序（链表的第1个节点是根，前序遍历方便）
    public static void traversalBinaryTree(TreeNode root) {
        if (root != null) {
            System.out.print(root.data + " ");
            traversalBinaryTree(root.left);
            traversalBinaryTree(root.right);
        }
    }
}

　　

输出：

?
1
2
Binary Tree traversal:
1 2 4 5 3

　　

Python

在 Python 中，可以使用链表来实现二叉树的存储。这种方式通常被称为链表表示法（Linked List Representation）或链表嵌套方式（Linked List Nested Method）。这种表示法相对于数组或列表更灵活，因为它不需要预分配存储空间，并且可以轻松处理不规则的二叉树结构。

1. 二叉树节点的定义

首先，我们需要定义二叉树的节点结构。每个节点需要包括值和两个指向其左子树和右子树的指针。通常，我们使用类来表示节点，如下所示：

?
1
2
3
4
5
class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

　　

创建二叉树

要创建一个二叉树，您可以手动创建节点并连接它们，或者使用一个函数来构建整棵树。下面是一个简单的示例，演示如何创建一个二叉树：

# 创建节点
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

在上面的示例中，我们创建了一个包含五个节点的二叉树。

遍历二叉树

一旦创建了二叉树，您可以使用递归或其他遍历算法来访问二叉树的节点。下面是几种常见的二叉树遍历方式：

先序遍历（Preorder Traversal）

先序遍历是一种深度优先遍历方式，它首先访问根节点，然后依次遍历左子树和右子树。下面是先序遍历的示例代码：

?
1
2
3
4
5
6
7
def preorder_traversal(node):
    if node:
        print(node.value)
        preorder_traversal(node.left)
        preorder_traversal(node.right)
 
preorder_traversal(root)

　　

中序遍历（Inorder Traversal）

中序遍历也是深度优先遍历方式，它首先遍历左子树，然后访问根节点，最后遍历右子树。下面是中序遍历的示例代码：

?
1
2
3
4
5
6
7
def inorder_traversal(node):
    if node:
        inorder_traversal(node.left)
        print(node.value) 
        inorder_traversal(node.right)
 
inorder_traversal(root)

　　

后序遍历（Postorder Traversal）

后序遍历是深度优先遍历方式，它首先遍历左子树，然后遍历右子树，最后访问根节点。下面是后序遍历的示例代码：

?
1
2
3
4
5
6
7
def postorder_traversal(node):
    if node:
        postorder_traversal(node.left)
        postorder_traversal(node.right)
        print(node.value)
 
postorder_traversal(root)

　　

示例

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None
 
 
class BinaryTree:
 
    def __init__(self, value):
        self.root = TreeNode(value)
 
    def insert(self, data):
        # 创建节点
        insertNode = TreeNode(data)
        if self.root is None:
            self.root = insertNode
        # 存储节点，用于遍历
        arr = [self.root]
        while len(arr) > 0:
            tmp = arr.pop(0)  # pop不指定索引，默认删除最后1个元素
            if tmp.left is None:
                tmp.left = insertNode
                return
            else:
                arr.append(tmp.left)
            if tmp.right is None:
                tmp.right = insertNode
                return
            else:
                arr.append(tmp.right)
 
 
'''
前序遍历
'''
def preorder_traversal(node):
    if node:
        print(node.value, end=" ")
        preorder_traversal(node.left)
        preorder_traversal(node.right)
 
 
'''
中序遍历
'''
def inorder_traversal(node):
    if node:
        inorder_traversal(node.left)
        print(node.value, end=" ")
        inorder_traversal(node.right)
 
 
'''
后序遍历
'''
def postorder_traversal(node):
    if node:
        postorder_traversal(node.left)
        postorder_traversal(node.right)
        print(node.value,end=" ")
 
 
tree = BinaryTree(1)
tree.insert(2)
tree.insert(3)
tree.insert(4)
tree.insert(5)
preorder_traversal(tree.root)
print()
inorder_traversal(tree.root)
print()
postorder_traversal(tree.root)

　　

输出：

?
1
2
3
1 2 4 5 3
4 2 5 1 3
4 5 2 3 1

　　

最佳实践

在使用链表表示法来实现二叉树时，一些最佳实践包括：

  1. 使用节点类来表示二叉树节点，这可以使代码更加清晰和模块化。

  2. 使用递归算法来遍历二叉树，因为它们通常更简洁和易于理解。

  3. 添加适当的错误处理和条件检查，以避免在访问空节点时出现错误。

  4. 使用合适的数据结构，如栈，来实现非递归遍历算法。

  5. 考虑添加其他属性或方法来处理特定的二叉树操作，如查找、插入和删除节点。

希望这些示例和最佳实践可以帮助您开始使用链表表示法来实现和操作二叉树。链表表示法在处理不规则或动态变化的二叉树结构时非常有用，因为它允许您轻松地连接和重组节点

 

posted @   Allen_Hao  阅读(151)  评论(0)  编辑  收藏  举报
相关博文：
· 数据结构之树（二叉树的存储方式之数组）
· 数据结构之树（遍历）
· 数据结构-树
· 十-2, Java实现顺序存储二叉树的遍历
· Java 数据结构 - 树（Tree）
阅读排行：
· 无需6万激活码！GitHub神秘组织3小时极速复刻Manus，手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火，是硬核还是营销？
· 终于写完轮子一部分：tcp代理 了，记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛（1）
点击右上角即可分享
微信分享提示