集成模型之Adaboost算法

AdaBoost 的全称为Adaptive Boosting。之所以称为 Adaptive 是由于下一轮分类器的训练样本权重会随上一轮分类器的分类效果做相应的调整。基于之前学过的 Boosting 算法，整个 Adaboost 迭代算法可以简化为以下三步：

1.初始化训练样本的权值 \(D_{0}\) 。则每一个训练样本的权重被初始化为 \(\frac{1}{m}\) ，其中 m 为样本的数量。
2.迭代训练弱分类器。在迭代过程中，需要对样本权重 \(D_{i}\) 进行更新。如果某个样本点已经被准确地分类，那么在训练下一个弱分类器时，就会降低它的权值；相反，如果该个样本点没有被准确地分类，就会提高它的权值。
3.将各个弱分类器加权平均得到强分类器。误差率 e 低的弱分类器权重 \(\alpha\) 较大，误差率 e 高的弱分类器权重 \(\alpha\) 较小。

相信大家看完以上算法，会有以下三个疑问：

1. 如何定义弱分类器的误差率 e ?
2. 如何定义弱学习器的权重 \(\alpha\) ?
3. 如何定义样本的权重 D ?
   下面我们来回答以上三个疑问。

1. Adaboost 的三个问题
假设我们的训练集样本是
\(T=(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m})\)
训练集的在第 k 个弱学习器的输入样本权重为：
\(D(k) = (w_{k1},w_{k2},...,w_{km})\)
其中基分类器的输入样本权重初始化为：
\(D(1) = (w_{11},w_{12},...,w_{1m}) = (\frac{1}{m},\frac{1}{m},...,\frac{1}{m})\)
对于第一个问题，第 k 个弱分类器 \(G_{K}(X)\) 误差率为
\(e_{k} = P(G_{k}(x_{i} \neq y_{i}) = \sum_{i=1}^m w_{ki} I(G_{k}(x_{i} \neq y_{i})\)
其中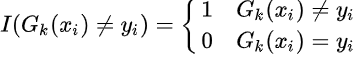

https://zhuanlan.zhihu.com/p/38507561 （集成模型之Adaboost算法）
https://zhuanlan.zhihu.com/p/29765582 （GBDT的原理）