Teacc
Object-Oriented unit 1 表达式求导

Object-Oriented unit 1
表达式求导

一、第一次作业

1.需求分析

设定的形式化表述

  • 表达式 \(\rightarrow\) 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
  • 项 \(\rightarrow\) [加减 空白项] 因子 | 项 空白项 * 空白项 因子
  • 因子 \(\rightarrow\) 变量因子 | 常数因子
  • 变量因子 \(\rightarrow\) 幂函数
  • 常数因子 \(\rightarrow\) 带符号的整数
  • 幂函数 \(\rightarrow\) x [空白项 指数]
  • 指数 \(\rightarrow\) ** 空白项 带符号的整数
  • 带符号的整数 \(\rightarrow\) [加减] 允许前导零的整数
  • 允许前导零的整数 \(\rightarrow\) (0|1|2|…|9)
  • 空白项 \(\rightarrow\)
  • 空白字符 \(\rightarrow\) （空格） | \t
  • 加减 \(\rightarrow\) + | -

其中{}表示0个、1个或多个，[]表示0个或1个，|表示多个之中选择。

式子的具体含义参照其数学含义。

若输入字符串能够由“表达式”推导得出，则输入字符串合法。

注意点

  • 无需检测format正确性

2. 实现方案

本次作业我基本使用正则表达式处理。
处理输入步骤如下：

  • 首先根据形式化表述确定所有的基本类
    • 表达式Expr，项Term，因子Factor
    • Factor类设计子类Constant和PowerFunc
    • 在每一个类中设计一个容器Arrylist用来保存更下层的类
  • 根据文法确定基本类对应正则表达式
  • 预处理字符串
    • 将各项之间[+-]项尽量压缩成一个[+-]
    • 删除空白项
    • 将**替换为^，以达到处理时和*有明显区分界限
    • 将幂上的指数进行基本化简，去掉+
  • 利用split函数，根据+分开Expr中的每一个Term
  • 利用split函数，根据*分开Term中的每一个Factor
  • 使用正则表达式匹配Factor，然后匹配到具体的Factor类中

处理求导方法：

  • 利用求导规则解得相同类的结果，并转化为字符串即可
    • 此处重写toString函数
  • 根据处理输入的逆过程拼接各个Factor和Term
//以下为正则表达式的写法
    private static final String isBlank = "[\\t ]*";
    private static final String isConstant = "[+-]?[0-9]+";
    private static final String isPowerfunc = "x(" + isBlank + "\\*\\*" + isBlank + "(" + isConstant + "))?";
    private static final String isFactor = "(" + isPowerfunc + ")|(" + isConstant + ")";
    private static final String isTerm = "([+-]" + isBlank + ")?(" + isFactor + ")" +
            "((" + isBlank + "\\*" + isBlank + ")(" + isFactor + "))*";
    private static final String isExpr = isBlank + "([+-]" + isBlank + ")?(" + isTerm + ")" + isBlank +
            "([+-]" + isBlank + "(" + isTerm + ")" + isBlank +")*";

3. 具体实现困难

实际上在我本人的操作过程中，第一次作业并未完成。
原因在于，我一直在尝试根据正则表达式Matcher.find()匹配答案，而实际上无论是贪心或者非贪心的匹配，库函数均只能匹配到某一项(Term)紧邻的一项或者最后一项，而无法通过递归方法Matcher.group()函数匹配所有项。
在和往届学长讨论之后，我使用字符串预处理，在第一次作业关闭之后才完成任务，并且没有充分的测试。
这次作业整体对我来说是失败的。

二、第二次作业

1.需求分析

设定的形式化表述

  • 表达式 \(\rightarrow\) 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
  • 项 \(\rightarrow\) [加减 空白项] 因子 | 项 空白项 * 空白项 因子
  • 因子 \(\rightarrow\) 变量因子 | 常数因子 | 表达式因子
  • 变量因子 \(\rightarrow\) 幂函数 | 三角函数
  • 常数因子 \(\rightarrow\) 带符号的整数
  • 表达式因子 \(\rightarrow\) '(' 表达式 ')'
  • 幂函数 \(\rightarrow\) x [空白项 指数]
  • 三角函数 \(\rightarrow\) sin 空白项 '(' 空白项 x 空白项 ')' [空白项 指数] | cos 空白项 '(' 空白项 x 空白项 ')' [空白项 指数]
  • 指数 \(\rightarrow\) ** 空白项 带符号的整数
  • 带符号的整数 \(\rightarrow\) [加减] 允许前导零的整数
  • 允许前导零的整数 \(\rightarrow\) (0|1|2|…|9)
  • 空白字符 \(\rightarrow\) （空格） | \t
  • 空白项 \(\rightarrow\)
  • 加减 \(\rightarrow\) + | -

注意点：

  • 在第一次作业的基础上引入了三角函数求导
  • 允许表达式嵌套(较前几届作业的难点)
  • 仍然无需检测format

2. 实现方案

  • 由于我难以在前一次的作业基础上改进，所以完全重构，虽然看起来是一个退化的重构。

具体实现方案如下：(一言以蔽之，一律通过括号识别)

  • 建立一个统一的表达式类Expr，其成员变量为如下图

  • 对输入字符串进行预处理，根据运算优先级自优先向落后添加括号。

  • 遍历字符串

  • 对每一个识别出来的左括号，找到对应的右括号

  • 右括号后面应该紧跟一个运算符

  • 将括号内的部分作为Expression的左子树，将运算符后面的部分作为右子树，将运算符和对应字符串存储。

  • 对求导方法，我使用大量的switch进行特判并运算

3. 完成后感想

i)困难

我基本使用面向过程的方法，致使出现的bug必须一个个修复，过程纷繁复杂。

ii)强测和互测阶段的问题

我的求导过程十分简单，并且只进行了极少量的优化。最终出现了2个bug：

  • 化简表达式时将所有的0*某一项后面全部删除，导致会出现丢失。例如50*某一项，5会变成结尾。
  • 当嵌套表达式因子的时候，如果出现*，会产生莫名中断。在删掉一些优化之后程序正确。

关于优化

由于本人能力太差，所以没有进行任何优化，也没有考虑过重构，毕竟这种单类方法也能够解决求导方法。但是由于大量的判断，致使方法长度超标，代码风格分太低。

三、第三次作业

1. 需求分析

  • 表达式 \(\rightarrow\) 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
  • 项 \(\rightarrow\) [加减 空白项] 因子 | 项 空白项 * 空白项 因子
  • 因子 \(\rightarrow\) 变量因子 | 常数因子 | 表达式因子
  • 变量因子 \(\rightarrow\) 幂函数 | 三角函数
  • 常数因子 \(\rightarrow\) 带符号的整数
  • 表达式因子 \(\rightarrow\) '(' 表达式 ')'
  • 三角函数 \(\rightarrow\) sin 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数] | cos 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数]
  • 幂函数 \(\rightarrow\) x [空白项 指数]
  • 指数 \(\rightarrow\) ** 空白项 带符号的整数
  • 带符号的整数 \(\rightarrow\) [加减] 允许前导零的整数
  • 允许前导零的整数 \(\rightarrow\) (0|1|2|…|9)
  • 空白字符 \(\rightarrow\) （空格） | \t（水平制表符）
  • 空白项 \(\rightarrow\)
  • 加减 \(\rightarrow\) + | -

值得注意的是，本次作业加入了表达式的嵌套，并且严格规定了格式，需要进行格式筛查。

2. 实现方案

本次作业在第二次基础上改进完成，没有进行重构，只是加入了有关三角函数复合的求导。对于格式筛查问题，我对于指导书给出的样例进行了少数特判，对于格式筛查不够严厉，但是也通过了中测。在互测阶段，由于输入长度不大于40和不允许格式错误输入的限制，我在互测没有出现任何问题(当然也是有可能自己所在的组的检测能力不够)。

代码长度分析

全部类分析

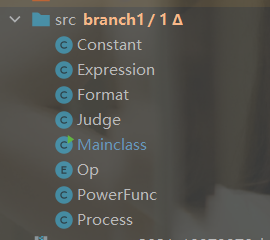
  • Constant:用来提取幂函数的指数
  • Expression:用来存储表达式
  • Format:存储少量的正则表达式用来匹配
  • Judge:用来判断格式问题
  • Op:运算符枚举变量
  • PowerFunc:针对幂函数进行求导
  • Process:处理输入输出格式问题

出现的问题：在强测阶段，没有进行特判的格式问题全部出错。

四、互测

我没有花时间构建评测机和构造数据，对于自己的bug也是对症下药单步调试，没有什么经验或者教训。

五、本单元的总结与体会

这是初次接触OOp语言，我对于面向对面的理解不够深刻，也没有很多机会去学习了解，而作业难度太大，导致我第一次作业就未完成。当时发现只剩20分钟就截止而我还有很多没有完成时内心很沮丧，并且充满了恐惧。

但是这之后我并没有放弃，而是和一个关系好的学长一起学习，向他请教怎么完成作业，星期一一直交流到十一点。在走出正则表达式匹配的误区之后，我果断选择了重构，并且在周三完成了第一次作业。

实际上，我个人认为这次作业并不难，但是我身边所有人都告诉我要去使用正则表达式，包括指导书也有这种误导，让我陷入了原地转圈的误导。私以为指导书不如去掉这种指导，这是完全的误导。

而在后面的作业，我由于自己没有编程经验，采取了预处理+遍历+结果处理字符串的方法来解决这一问题，导致的结果也看得见：我写了400多行的Process类。并且由于第一次给我的打击，我已经不愿意做任何优化。其实我相信我是有一定能力做少量优化的，只是课程组不合适的安排消耗了我的学习动力。

写在最后的是，我认为OO课程组的教学安排并不是十分合理的，这一点在与班会上班主任熊桂喜教授也有所交流。我本人很愿意为努力学好一门课程做出努力，但是不愿意做出无谓的付出。我认为学习一定是从模仿开始，而后才能更新出自己的创新。而课程组所谓“学术不端”检测虽然能一定程度上克服抄袭问题，但是对真正能收获好的代码架构、风格的学习方法也索性禁绝了，替代的是大部分学生无意义的学习。
我尤其想说的是，并不是所有的学生都有超强的独立自学能力，助教本身是课程的佼佼者，只能代表前10%或者20%的学生。如果课程组一味只在意助教的思维而忽略的大量平凡而普通的初学者，这只能得出越来越不好的学生评价。
本学期c++课程刘禹老师认为以学生抬头率作为评价课程讲的怎么样的标准，那么OO这门课的抬头率究竟如何呢？

posted on 2021-03-27 10:49  Teacc  阅读(108)  评论(0)    收藏  举报

博客园  ©  2004-2026
浙公网安备 33010602011771号 浙ICP备2021040463号-3 Powered By博客园