【趣题】水题-勾选格子（状态压缩+模拟）
写在前面
感谢朋友圈神秘大佬的纠正！勾选的格子上的条件必须满足，不勾选的格子上的条件必须不满足！修改了代码。
恕我愚笨，昨天我以为这类题根本没法推理，但事实上各位大佬很快就推出来了。如果你希望自己推理或尝试，请先不要用暴力解法……
题目
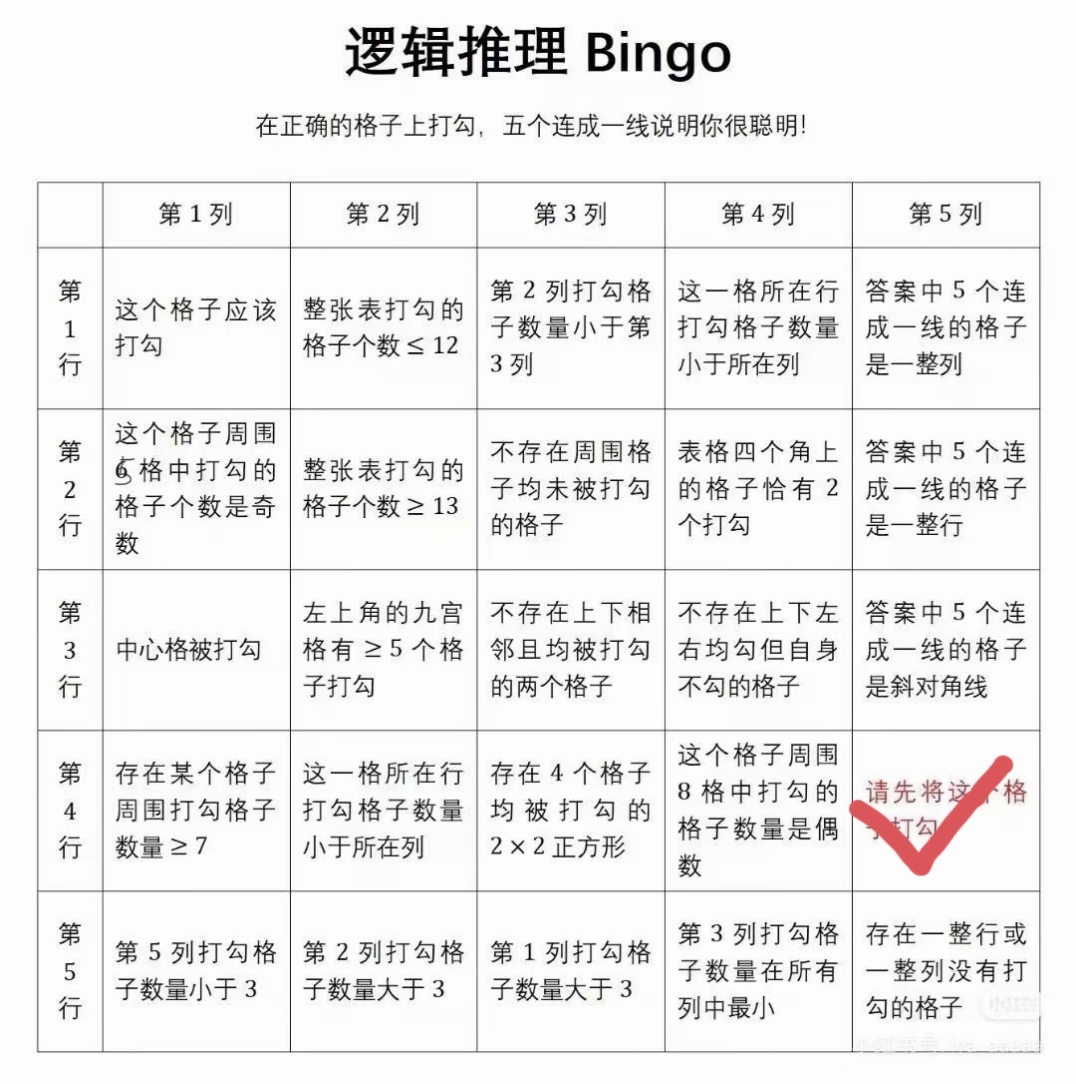
今日闲来无事，这是我在朋友圈看到的一个智力小游戏。
你可以试着推理，也可以猜一下：哪一行或哪一列或哪条对角线，是需要被连成一线的？答案在文末揭晓。
当我试着推理，我发现这个答案非常难找，因为每个格子是否勾选影响着很多格子的正确性，从第\(4\)行第\(5\)列开始也无法进行什么推理，几乎只能靠感觉？（如果有神能靠推理做出来，你将是我的偶像）。但是，作为计算机学生，也可以写个程序来解决这个问题。
思路
状态压缩
一共有\(25\)个格子，每个格子有“选”和“不选”两种情况，所以这就是典型的“二进制状态压缩”。设选的符号为\(1\)，不选为\(0\)，则可以画出一个包含\(0\)和\(1\)的地图：
\[\begin{aligned}
01010 \\
10101 \\
00001 \\
00101 \\
10100
\end{aligned}
\]
对于这个地图，我们可以将其写成一串：
\[0101010101000010010110100
\]
将上面这个状态压缩成一个二进制数，再转为十进制，我们便得到了状态压缩后的值：
\[(0101010101000010010110100)_2 = (11175092)_{10}
\]
每一个十进制数只对应着一个二进制数，则压缩前与压缩后的状态形成双射，唯一对应，所以我们只需要枚举\(0\)到\(2^{25}-1\)内的所有十进制数对应的状态即可遍历所有情况。
设置\(check(sta)\)函数，用于检测状态\(sta\)是否合格。输出所有可行解。在只考虑检查被勾选的格子的条件时，得到了\(2\)个解。
时间复杂度分析
每个格子只有“选”和“不选”两种情况，共\(25\)个格子，所以程序时间复杂度为\(O(2^n)\)即\(2^{25}\)，但常数较大，实测程序运行时间约\(3.4\)秒。
当然，第四行第五列是必选的，第一行第一列是可选可不选的，所以你可以只枚举剩下的格子，状态数将降为\(2^{23}\)，节省\(\frac{3}{4}\)的时间。
还有，如果你很聪明，发现题目要求，正解中总有某一行或某一列或某对角线需要全被选，那么你可以枚举这\(12\)条直线，在每次枚举时又减少了\(4\)或\(5\)个格子，则状态数又降为原来的\(\frac{1}{2^{4}}\)，会节省很多时间！（但代码又变复杂了，我就不写了）
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using ld = long double;
using dd = double;
i64 mp[5][5];
i64 dx[] = {0, 1, 0, -1};
i64 dy[] = {1, 0, -1, 0};
i64 ddx[] = {-1, -1, -1, 0, 1, 1, 1, 0};
i64 ddy[] = {-1, 0, 1, 1, 1, 0, -1, -1};
i64 cases = 0;
bool il(i64 x, i64 y) {
return 0 <= x && x < 5 && 0 <= y && y < 5;
}
void print() {
cout << "Case" << ++cases << " : \n";
for (i64 i = 0; i < 5; i++) {
for (i64 j = 0; j < 5; j++)
if (mp[i][j])
cout << " 1 ";
else
cout << " 0 ";
cout << "\n";
}
}
void check(i64 sta) {
for (i64 i = 0; i < 5; i++)
for (i64 j = 0; j < 5; j++)
mp[i][j] = ((sta & (1 << (i * 5 + j))) != 0);
//4 - 5：请先将这个格子打勾
if (!mp[3][4])
return;
//1 - 2：整张表打勾的各自个数 <= 12
i64 cnt = 0;
for (i64 i = 0; i < 25; i++)
cnt += mp[i / 5][i % 5];
if ((mp[0][1] && cnt > 12) || (!mp[0][1] && cnt <= 12))
return;
//1 - 3:第 2 列打勾格子数量小于第 3 列
i64 cnt_col_2 = 0, cnt_col_3 = 0;
for (i64 i = 0; i < 5; i++) {
cnt_col_2 += mp[i][1];
cnt_col_3 += mp[i][2];
}
if ((mp[0][2] && cnt_col_2 >= cnt_col_3) || (!mp[0][2] && cnt_col_2 < cnt_col_3))
return;
//1 - 4：这一格所在行打勾格子数量小于所在列
i64 cnt_col_4 = 0, cnt_row_1 = 0;
for (i64 i = 0; i < 5; i++) {
cnt_col_4 += mp[i][3];
cnt_row_1 += mp[0][i];
}
if ((mp[0][3] && cnt_row_1 >= cnt_col_4) || (!mp[0][3] && cnt_row_1 < cnt_col_4))
return;
//1 - 5：答案中 5 个连成一线的格子是一整列
bool yes = 0;
for (i64 i = 0; i < 5; i++) {
if (mp[0][i] && mp[1][i] && mp[2][i] && mp[3][i] && mp[4][i])
yes = 1;
}
if (mp[0][4] ^ yes)
return;
//2 - 1：这个格子周围 5 格中打勾的格子个数是奇数
i64 cnt_2_1 = mp[0][0] + mp[0][1] + mp[1][1] + mp[2][1] + mp[2][0];
if ((mp[1][0] && !(cnt_2_1 & 1)) || (!mp[1][0] && (cnt_2_1 & 1)))
return;
//2 - 2：整张表打勾的格子个数 >= 13
if ((mp[1][1] && cnt < 13) || (!mp[1][1] && cnt >= 13))
return;
//2 - 3：不存在周围格子均未被打勾的格子
yes = 1;
for (i64 i = 0; i < 5; i++)
for (i64 j = 0; j < 5; j++) {
i64 cnt = 0;
for (i64 idx = 0; idx < 4; idx++) {
i64 nx = i + dx[idx], ny = j + dy[idx];
if (il(nx, ny))
cnt += mp[nx][ny];
}
if (!cnt) {
yes = 0;
break;
}
}
if (mp[1][2] == yes)
return;
//2 - 4：表格四个角上的格子恰有 2 个打勾
i64 cnt_corner = mp[0][0] + mp[0][4] + mp[4][0] + mp[4][4];
if ((mp[1][3] && cnt_corner != 2) || (!mp[1][3] && cnt_corner == 2))
return;
//2 - 5：答案中 5 个连成一线的格子是一整行
yes = 0;
for (i64 i = 0; i < 5; i++) {
if (mp[i][0] && mp[i][1] && mp[i][2] && mp[i][3] && mp[i][4])
yes = 1;
}
if (mp[1][4] ^ yes)
return;
//3 - 1：中心格被打勾
if (mp[2][0] != mp[2][2])
return;
//3 - 2：左上角的九宫格有 >= 5个格子打勾
i64 cnt_gong = 0;
for (i64 i = 0; i < 3; i++)
for (i64 j = 0; j < 3; j++)
cnt_gong += mp[i][j];
if ((mp[2][1] && cnt_gong < 5) || (!mp[2][1] && cnt_gong >= 5))
return;
//3 - 3：不存在上下相邻且均被打勾的两个格子
yes = 0;
for (i64 i = 0; i < 4; i++)
for (i64 j = 0; j < 5; j++) {
if (mp[i][j] && mp[i + 1][j]) {
yes = 1;
break;
}
}
if ((mp[2][2] && yes) || (!mp[2][2] && !yes))
return;
//3 - 4：不存在上下左右均勾但自身不勾的格子
yes = 1;
for (i64 i = 1; i < 4; i++)
for (i64 j = 1; j < 4; j++) {
bool jun = 1;
for (i64 idx = 0; idx < 4; idx++) {
i64 nx = i + dx[idx], ny = j + dy[idx];
if (!mp[nx][ny]) {
jun = 0;
break;
}
}
if (jun && !mp[i][j]) {
yes = 0;
break;
}
}
if (mp[2][3] ^ yes)
return;
//3 - 5：答案中 5 个连成一线的格子是斜对角线
bool l_r = 1, r_l = 1;
for (i64 i = 0; i < 25; i += 6)
l_r = l_r & mp[i / 5][i % 5];
for (i64 i = 4; i < 25; i += 4)
r_l = r_l & mp[i / 5][i % 5];
yes = (l_r || r_l);
if (mp[2][4] ^ yes)
return;
//4 - 1：存在某个格子周围打勾格子数量 >= 7
yes = 0;
for (i64 i = 1; i < 4; i++)
for (i64 j = 1; j < 4; j++) {
i64 cnt = 0;
for (i64 idx = 0; idx < 8; idx++) {
i64 nx = i + ddx[idx], ny = j + ddy[idx];
cnt += mp[nx][ny];
}
if (cnt >= 7) {
yes = 1;
break;
}
}
if (mp[3][0] ^ yes)
return;
//4 - 2：这一格所在行打勾格子数量小于所在列
i64 cnt_row_4 = 0;
for (i64 i = 0; i < 5; i++)
cnt_row_4 += mp[3][i];
if ((mp[3][1] && cnt_row_4 >= cnt_col_2) || (!mp[3][1] && cnt_row_4 < cnt_col_2))
return;
//4 - 3：存在 4 个格子均被打勾的 2 * 2 正方形
yes = 0;
for (i64 i = 0; i < 4; i++)
for (i64 j = 0; j < 4; j++)
if (mp[i][j] && mp[i + 1][j] && mp[i][j + 1] && mp[i + 1][j + 1]) {
yes = 1;
break;
}
if (mp[3][2] ^ yes)
return;
//4 - 4：这个格子周围 8 格中打勾的格子数量是偶数
i64 cnt_4_4 = 0;
for (i64 idx = 0; idx < 8; idx++) {
i64 nx = 3 + ddx[idx], ny = 3 + ddy[idx];
cnt_4_4 += mp[nx][ny];
}
if ((mp[3][3] && (cnt_4_4 % 2)) || (!mp[3][3] && (cnt_4_4 % 2 == 0)))
return;
//5 - 1：第 5 列打勾格子数量小于 3
i64 cnt_col_5 = 0;
for (i64 i = 0; i < 5; i++)
cnt_col_5 += mp[i][4];
if ((mp[4][0] && cnt_col_5 >= 3) || (!mp[4][0] && cnt_col_5 < 3))
return;
//5 - 2：第 2 列打勾格子数量大于 3
if ((mp[4][1] && cnt_col_2 <= 3) || (!mp[4][1] && cnt_col_2 > 3))
return;
//5 - 3：第 1 列打勾格子数量大于 3
i64 cnt_col_1 = 0;
for (i64 i = 0; i < 5; i++)
cnt_col_1 += mp[i][0];
if ((mp[4][2] && cnt_col_1 <= 3) || (!mp[4][2] && cnt_col_1 > 3))
return;
//5 - 4：第 3 列打勾格子数量在所有列中最小
yes = (cnt_col_3 <= cnt_col_1 && cnt_col_3 <= cnt_col_2 && cnt_col_3 <= cnt_col_4 && cnt_col_3 <= cnt_col_5);
if (mp[4][3] ^ yes)
return;
//5 - 5：存在一整行或一整列没有打勾的格子
yes = 0;
for (i64 i = 0; i < 5; i++) {
if (!mp[i][0] && !mp[i][1] && !mp[i][2] && !mp[i][3] && !mp[i][4]) {
yes = 1;
break;
}
if (!mp[0][i] && !mp[1][i] && !mp[2][i] && !mp[3][i] && !mp[4][i]) {
yes = 1;
break;
}
}
if (mp[4][4] != yes)
return;
//题目要求：五个练成一线
yes = 0;
for (i64 i = 0; i < 5; i++) {
if (mp[i][0] && mp[i][1] && mp[i][2] && mp[i][3] && mp[i][4]) {
yes = 1;
break;
}
if (mp[0][i] && mp[1][i] && mp[2][i] && mp[3][i] && mp[4][i]) {
yes = 1;
break;
}
}
if (mp[0][0] && mp[1][1] && mp[2][2] && mp[3][3] && mp[4][4])
yes = 1;
if (mp[0][4] && mp[1][3] && mp[2][2] && mp[3][1] && mp[4][0])
yes = 1;
if (!yes)
return;
//找到可行解
print();
return;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
for (i64 sta = 0; sta < (1LL << 25); sta++)
check(sta);
return 0;
}
答案
以下是上面程序跑出来的所有答案，如有错误，欢迎纠正！
观察所有答案，第二行是正确答案！你猜对了吗？
点击查看所有答案
Case1 :
1 0 0 1 0
1 1 1 1 1
0 1 0 1 0
0 1 0 0 1
1 0 0 1 0
Case2 :
1 0 0 1 0
1 1 1 1 1
0 1 0 1 0
0 1 0 0 1
1 1 0 1 0
浙公网安备 33010602011771号