期末复习 | CUMT数据结构理论
数据结构复习
本文作者于2023年2月22号考试数据结构,为转专业班,单独出卷,难度不太具备参考性。
基础知识
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)
线性表
- 掌握顺序表的存储结构以及基本操作操作的代码实现以及它的优缺点——代码级
- 掌握顺序表的存储方式和基本操作的代码实现——代码级
- 掌握单链表的存储方式和基本操作的代码实现——代码级
链表头是整个链表的第一个节点,它不存放任何数据信息,不过它可以告诉我们第一个数据是从哪一个开始
单链表所需函数:
//正常插入
void insert(int k,int x){
e[idx] = x,ne[idx] = ne[k],ne[k] = idx,idx++;
}
//头插
void insert_head(int x){
e[idx] = x,ne[idx] = head,head = idx,idx++;
}
//删除
void del(int k){
ne[k] = ne[ne[k]];
}
- 单链表初始创建等的区别——由于头节点存在
- 循环链表和双向循环链表,掌握插入与删除(23年考题)
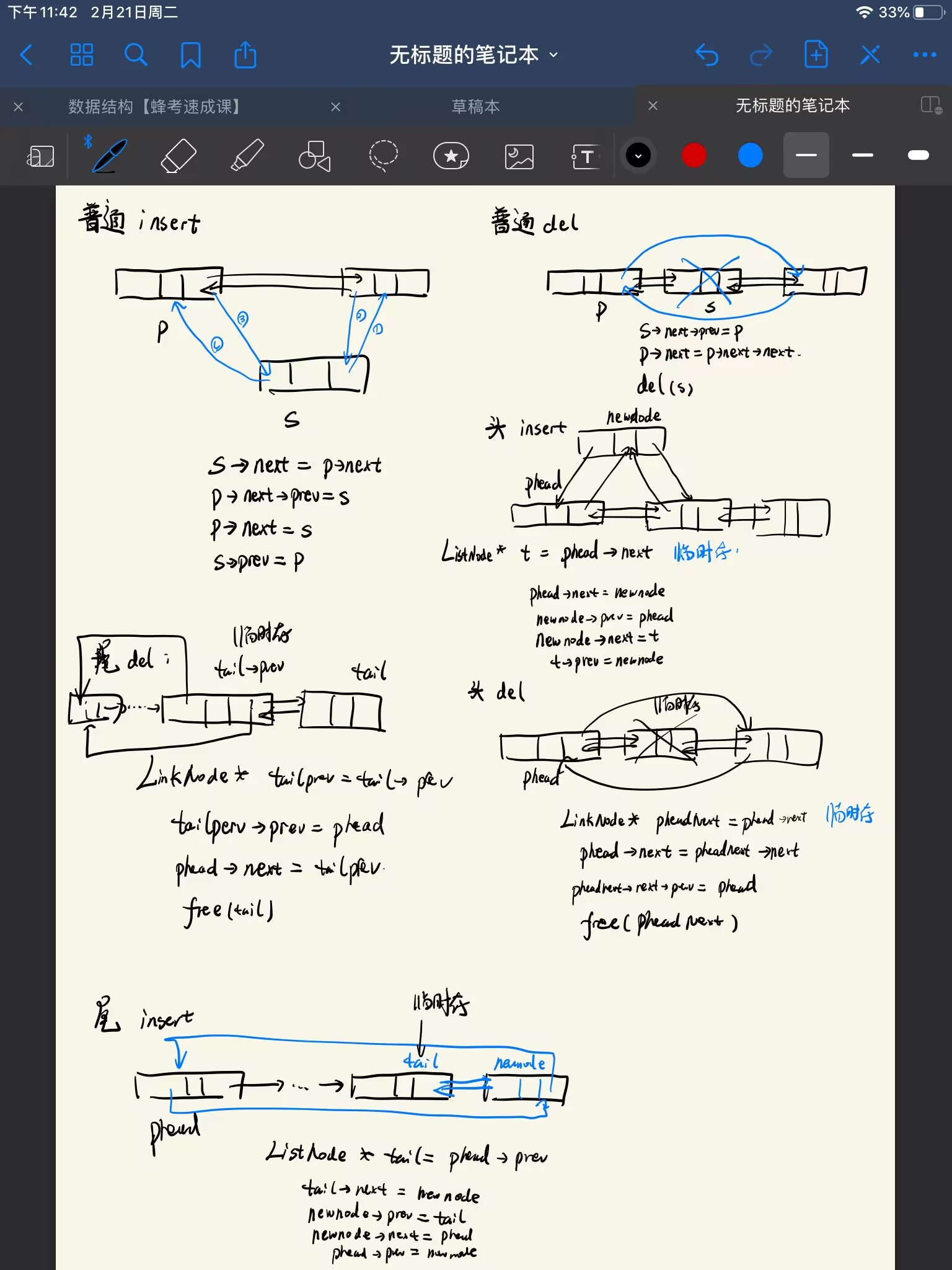
- 约瑟夫问题——循环链表
- 顺序栈和链式栈的实现——代码级
void init(){
ss = -1;
int stk[N];
}
void push(int x){
ss++;
stk[ss] = x;
}
void pop(){
ss--;
}
- 双向栈不需要看
- 给一个序列要知道可能的出战序列和不可能的情况以及出栈序列的个数
出栈序列的个数= (23年考题,要求求不可能的出栈序列)
$$ \frac{1}{n+1}C_{2n}^{n} $$
- 括号匹配:(23年考题)
for(int i=0;i<length;i++)
{
if(str[i]=='('||str[i]=='{'||str[i]=='[')
{
Push(S,str[i]);
}
else{
if((str[i]==')'||str[i]=='}'||str[i]==']')&&StackEmpty(S))return false;
char topElem;
Pop(S,topElem);
if(str[i]==')'&&topElem!='(')return false;
if(str[i]=='}'&&topElem!='{')return false;
if(str[i]==']'&&topElem!='[')return false;
}
}
return StackEmpty(S);
- 后缀表达式的求值
int main() {
string s;
cin>>s;
stack<int>st;
for(int i=0;i<s.size();i++){
if(s[i]=='+'||s[i]=='-'||s[i]=='*'||s[i]=='/'){
int num1=st.top();
st.pop();
int num2=st.top();
st.pop();
if(s[i]=='+')st.push(num2+num1);
if(s[i]=='-')st.push(num2-num1);
if(s[i]=='*')st.push(num2*num1);
if(s[i]=='/')st.push(num2/num1);
}else{
char ch=s[i];
string s2;
char s1[2]={ch,0};
s2=s1;
st.push(stoi(s2));
}
}
- 已知中缀表达式求后缀和前缀
先从右向左遍历中缀表达式,找到从右到左的第一个优先级最低的运算符来做二叉树的根,确定根之后那么它的左右子树基本确定,然后第二次遍历中缀表达式找第二优先级最低的运算符,然后根据刚刚的大致位置确定第二最低优先级运算符的位置
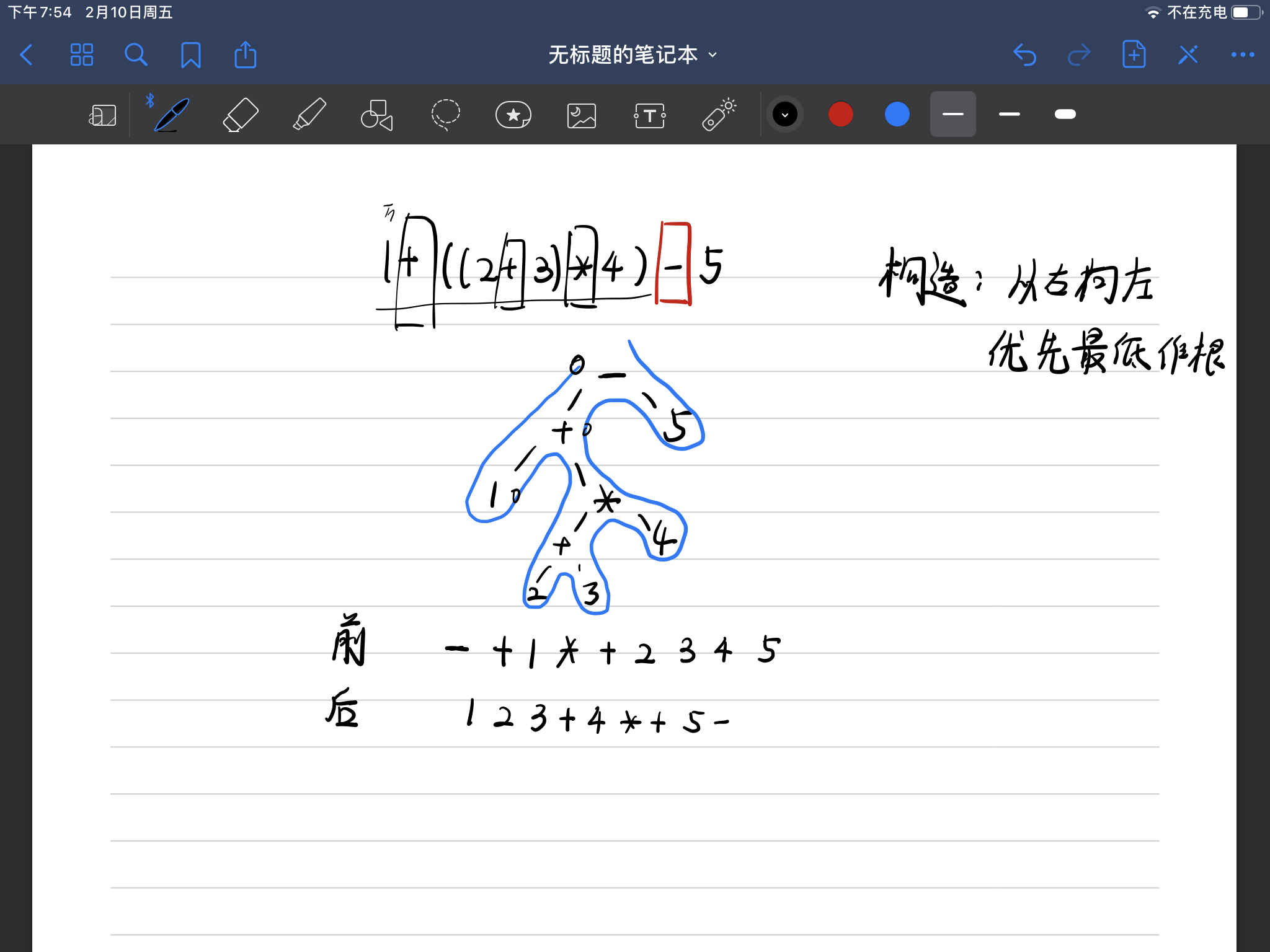
- 循环队列的顺序结构和链式结构--代码级
队头指针进1: front = (front + 1) % maxSize;
队尾指针进1: rear = (rear + 1) % maxSize;
队列初始化:front = rear = 0;
队空条件:front == rear;
队满条件:(rear + 1) % maxSize == front
-
了解对称矩阵的压缩存储过程
-
稀疏矩阵的存储结构
-
理解字符串的存储表示和提取子串简单模式匹配算法

树
- 基本术语要知道
- 树的逻辑结构
每个节点就只有唯一的前驱有零个或多个后继
- 二叉树———代码级
- 带空节点的先序建二叉树的方法
int BinTreeCreate(BitTree &BT)
{
char ch;
scanf("%c", &ch);
if(ch == '#') BT = NULL;
else{
BT = new BT;
BT->data = ch;
BinTreeCreate(BT->lchild);
BinTreeCreate(BT->rchild);
}
return 0;
}
- 给你一个先序列给你一个中序,要能够把这个二叉树画出来(不涉及到代码)(23年考题)

或者慢慢推(中左右,左中右)也行 - 二叉树遍历
void BinTraverse(BitTree BT)
{
if(BT == NULL) return;
printf("%c",BT->data);
if(BT->lchild != NULL)
BinTraverse(BT->lchild);
if(BT->rchild != NULL);
BinTraverse(BT->rchild);
}
//更换printf的位置即可得到中/后序遍历
- 一颗完全二叉树也要会非常熟练地算出度为零。度为一或度为二的节点个数以及他的深度,甚至于他的非叶子节点的个数都能算出来、
$$ n_{0} = n_{2} + 1 $$
- 树的子女兄弟存储方法,不需要代码理解
左指孩子,右指兄弟
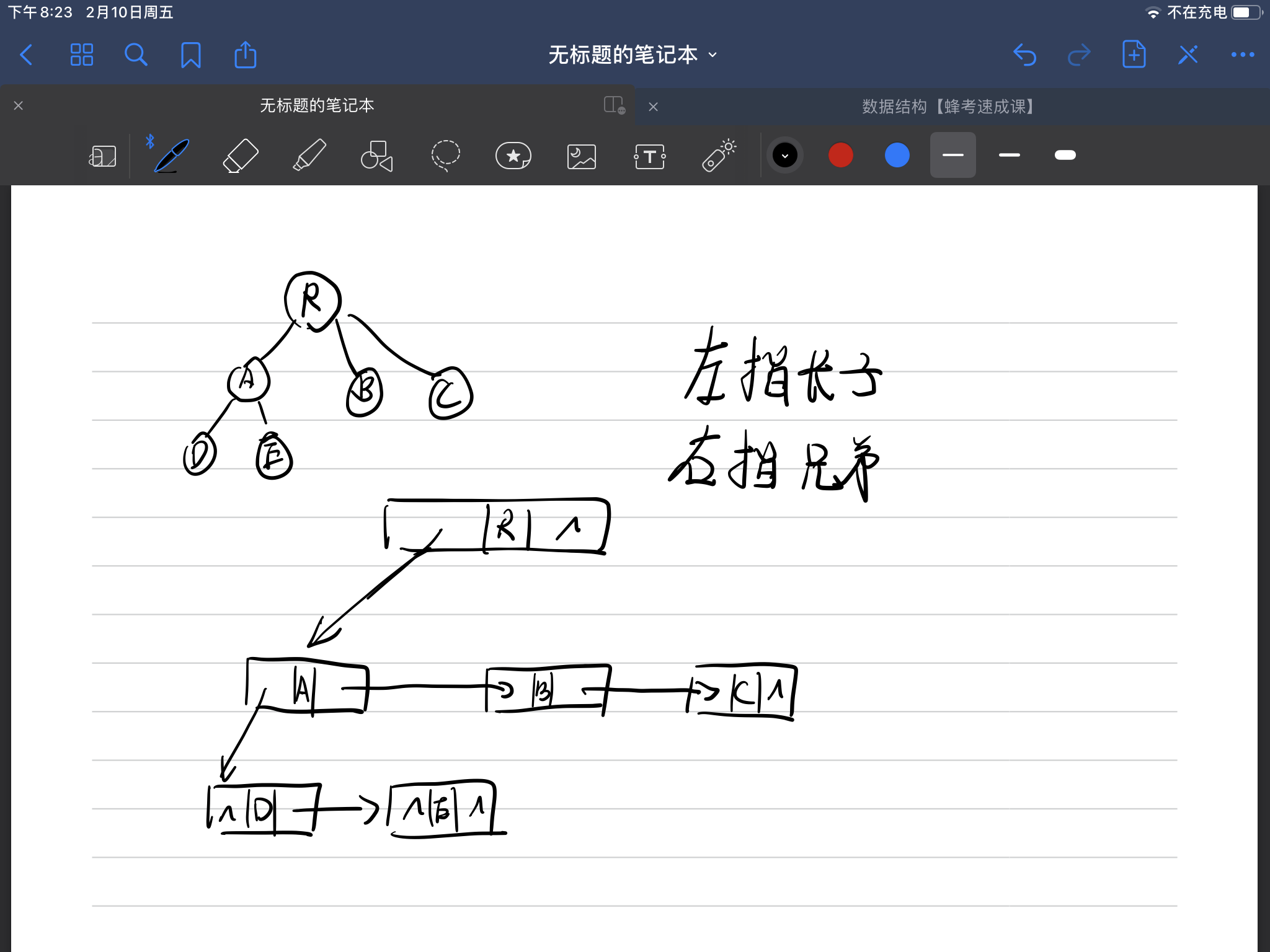
-
树和二叉树和森林的相互转换,不需要代码(23年考题)
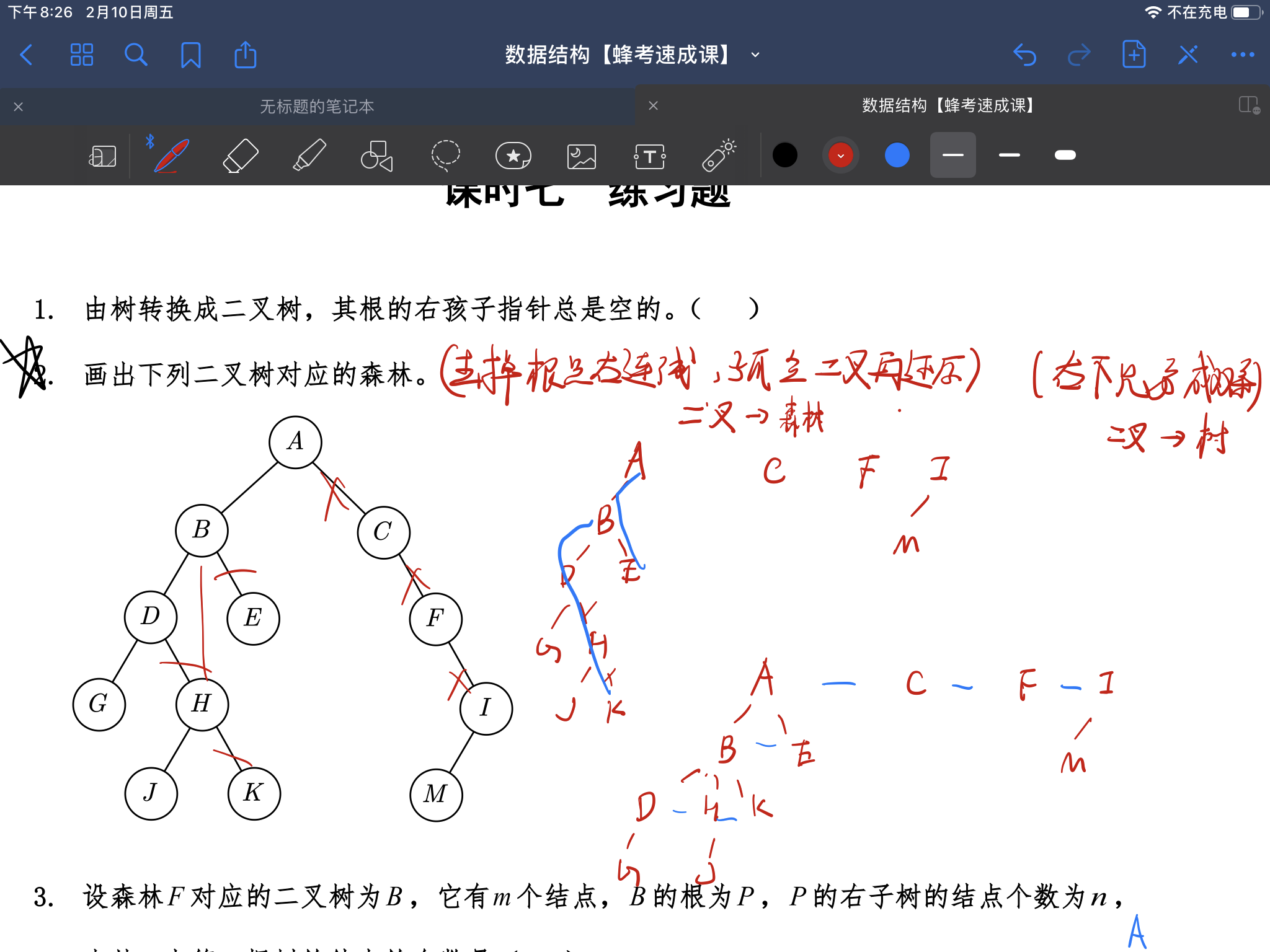
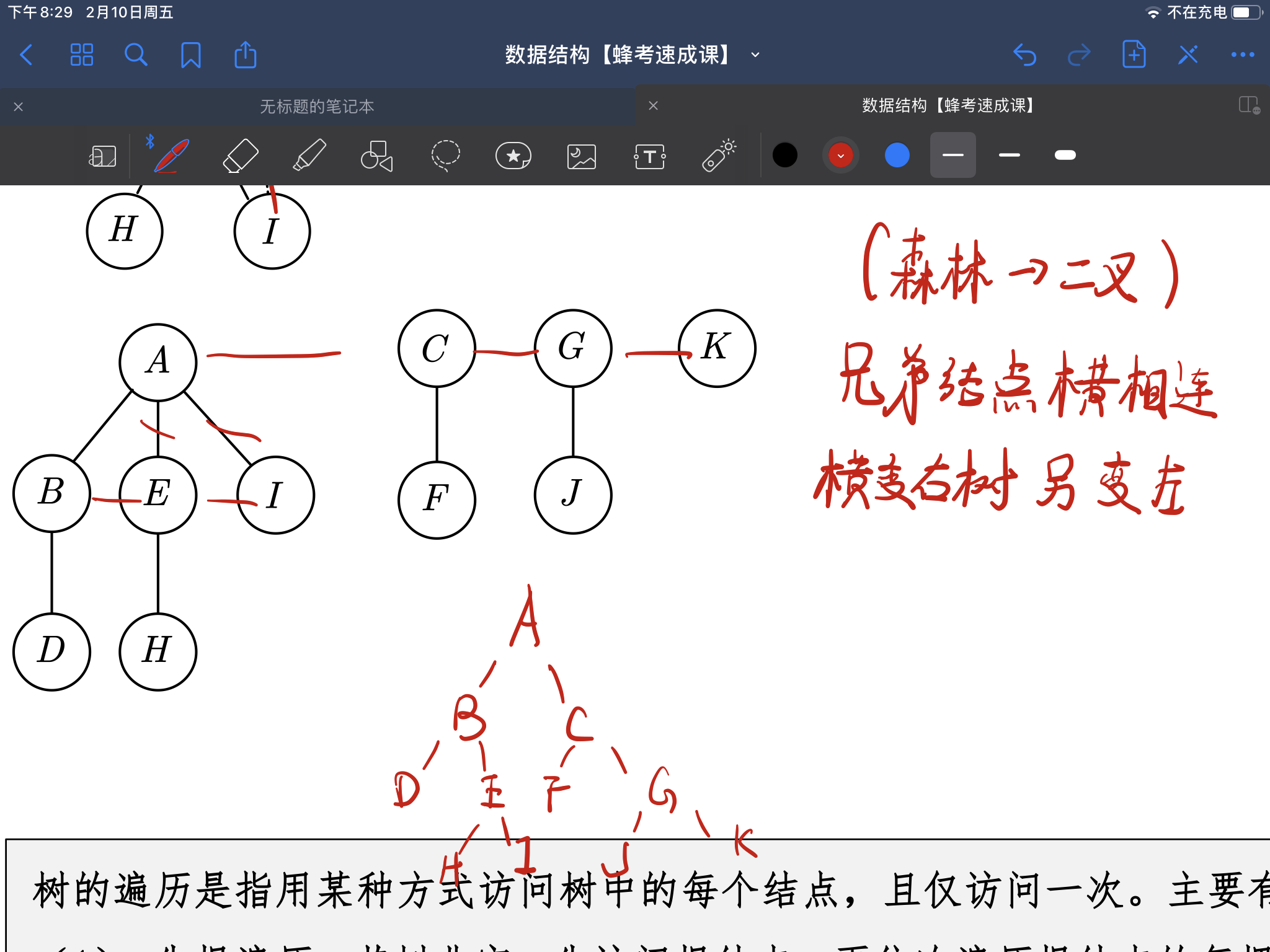
-
树/森林的深度优先

-
哈夫曼数和哈夫曼编码的过程(图有误,左0右1)(23年考题)
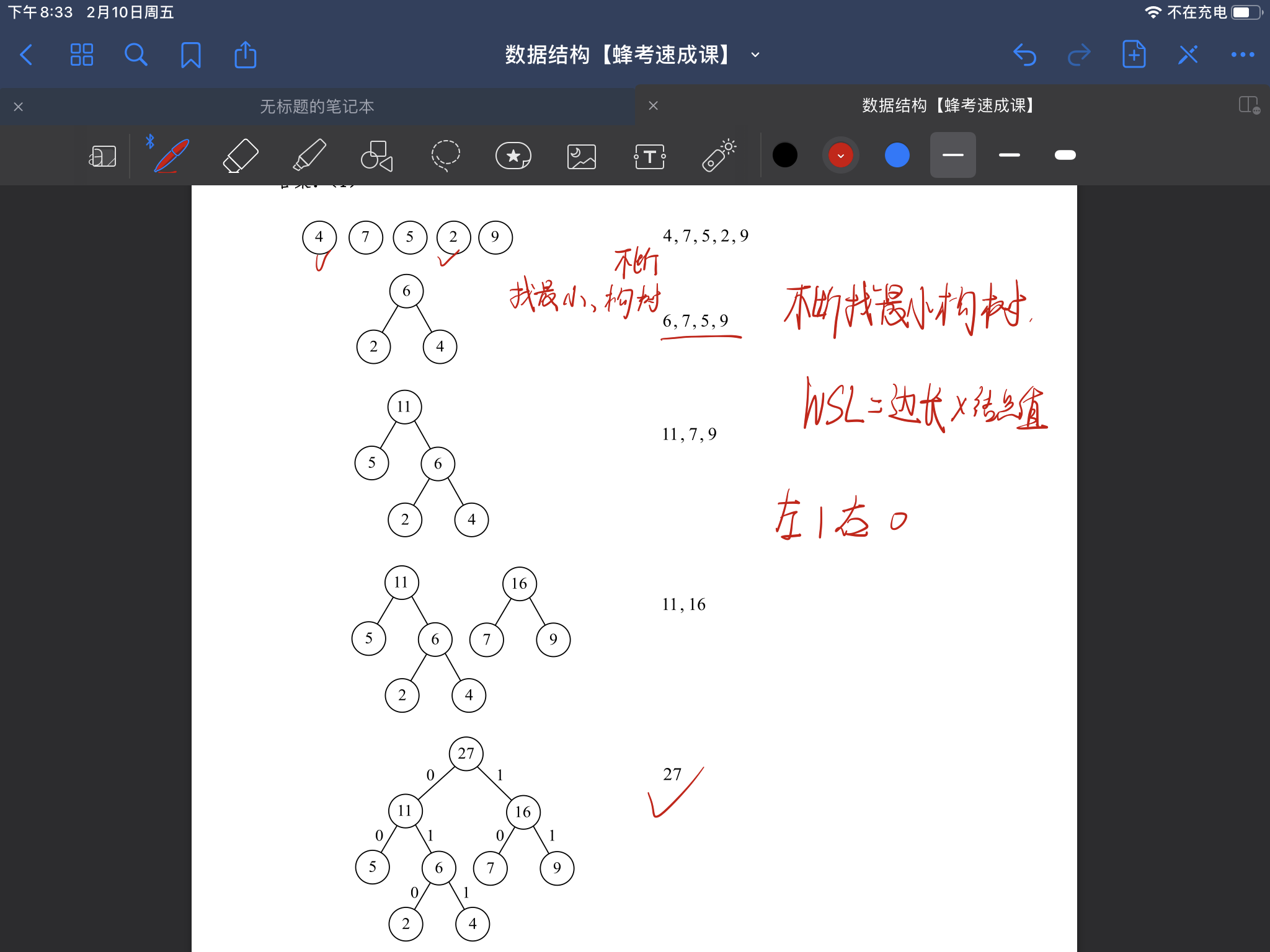
求解WPL:哈夫曼树代码实现
思路:维护一个小根堆,每次删除第一个和第二个元素,然后插入第一个和第二个元素的和
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
int main()
{
int n;
scanf("%d", &n);
priority_queue<int, vector<int>, greater<int>> heap;
while (n -- )
{
int x;
scanf("%d", &x);
heap.push(x);
}
int res = 0;
while (heap.size() > 1)
{
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
res += a + b;
heap.push(a + b);
}
printf("%d\n", res);
return 0;
}
- 判断是否是满二叉树
struct node {
int val;
node *left, *right;
};
int height(node *root) {
if (!root) return 0;
int left = height(root->left);
int right = height(root->right);
return max(left, right) + 1;
}
void count(node *root, int &sum) {
if (root) {
sum += 1;
count(root->left);
count(root->right);
}
}
bool isFBT(node *root) {
if (!root) return 1;
int sum = 0;
int h = height(root);
count(root, sum);
return sum == pow(2, h) - 1;
}
索引和散列
所有内容不需要代码级
- 散列查找技术的原理
散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f (key)
- 哈希函数的构建方法,重点掌握除留余数
线性探测。要会算查找成功(23年考题)和查找不成功,二次探测和双反,也只要会算查找成功就可以了
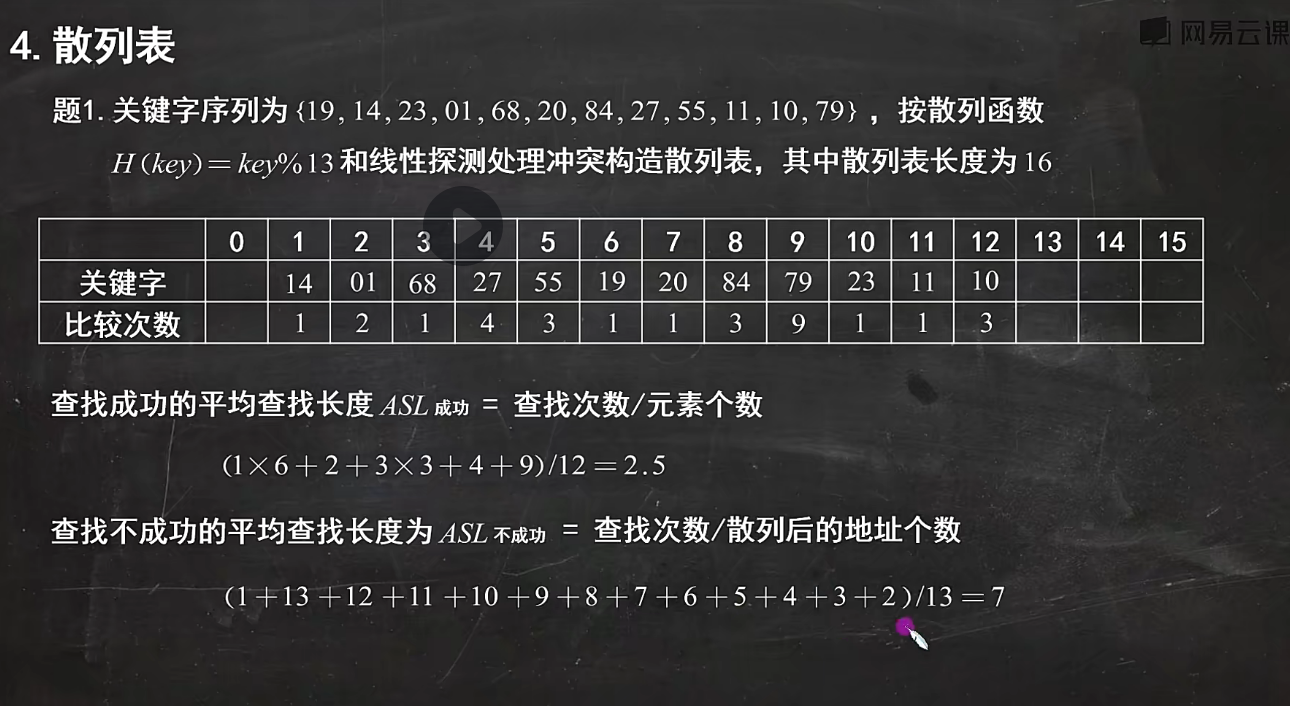
- 理解处理冲突开放定制法
当关键字key的哈希地址p=H(key)出现冲突时,以p为基础,产生另一个哈希地址p1,如果p1仍然冲突,再以p为基础,产生另一个哈希地址p2,…,直到找出一个不冲突的哈希地址pi ,将相应元素存入其中。
Hi=(H(key)+di)% m i=1,2,…,n
-
了解列地址法处理冲突的过程
-
理解决定哈希表查找ASL就是平均查找长度的因素:饱和因子Alpha
查找
- 顺序查找时间复杂度分析以及代码O(n),注意将i=0位置设成key
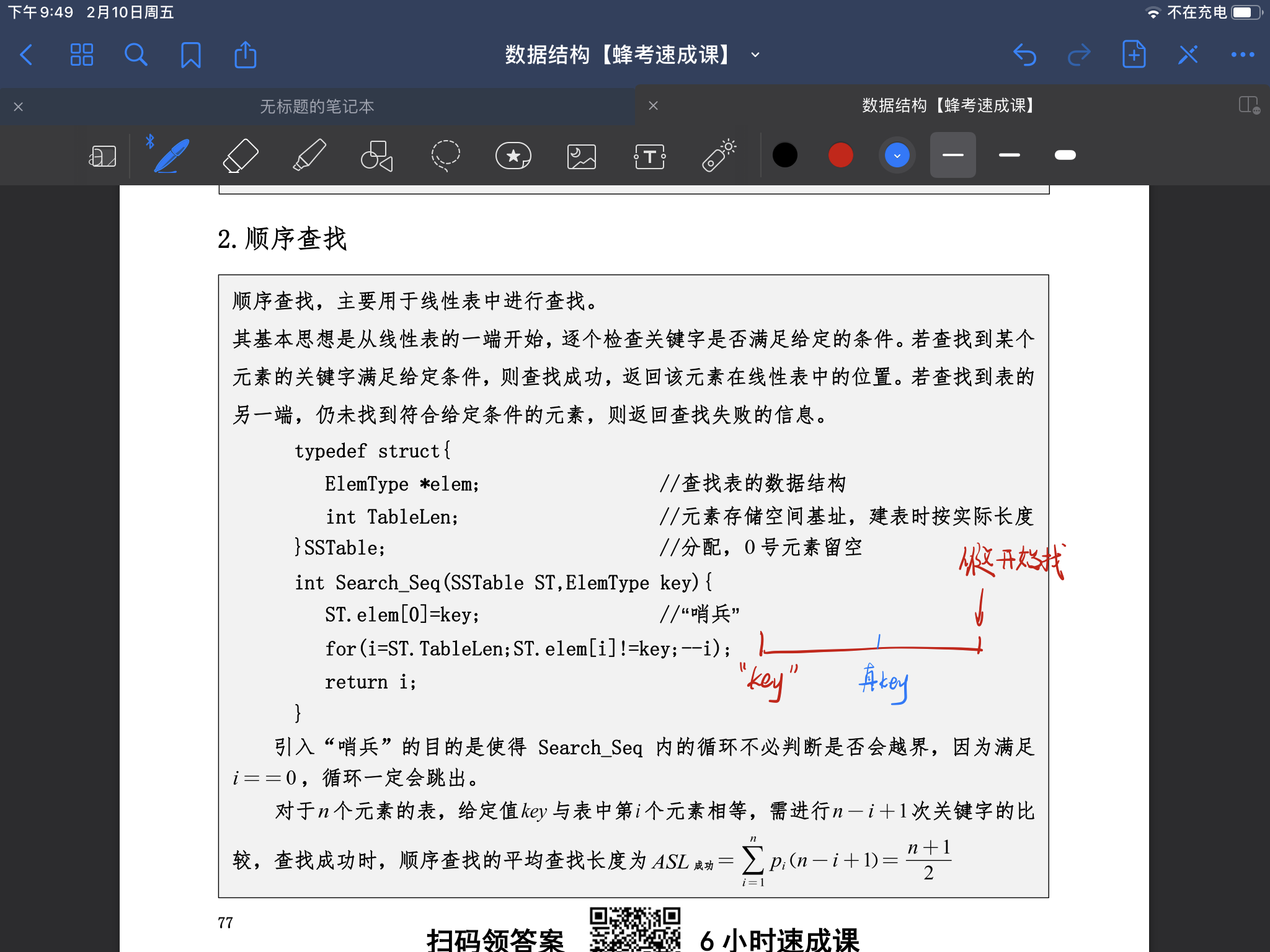
- 折半查找的代码以及时间复杂度分析(二分査找就是 折半查找 )
int a[N];
int bisect(int left,int right,int key){
left = 0;
right = a.size();
mid = (left + right) >> 1;
while(left < right){
if(a[mid] == key){
return mid;
}else if(a[mid] < key){
left = mid + 1;
}else if(a[mid] > key){
right = mid - 1;
}
}
return left;
}
- 二叉搜素判定树(23年考题,要计算ASL搜索成功)
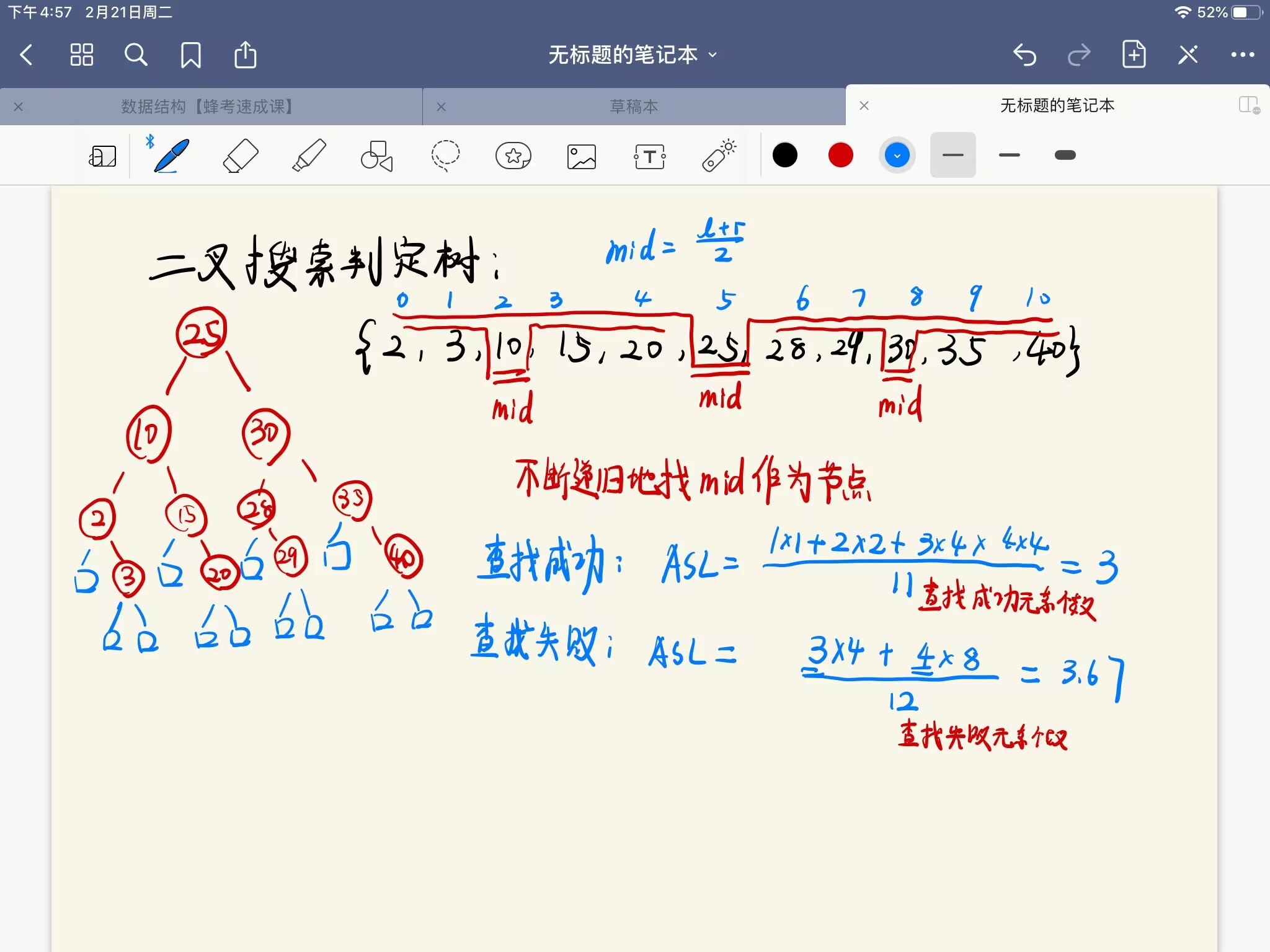
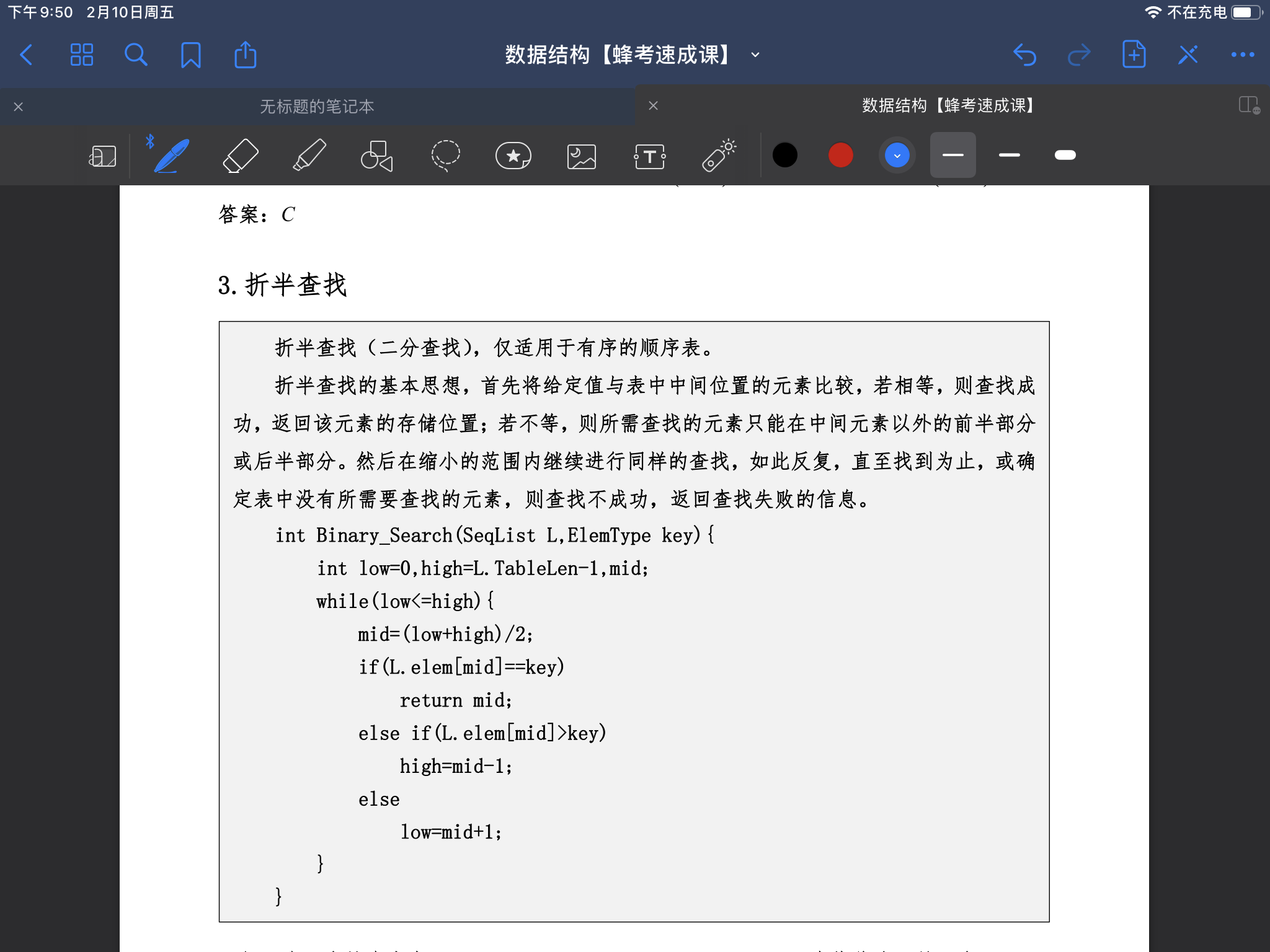
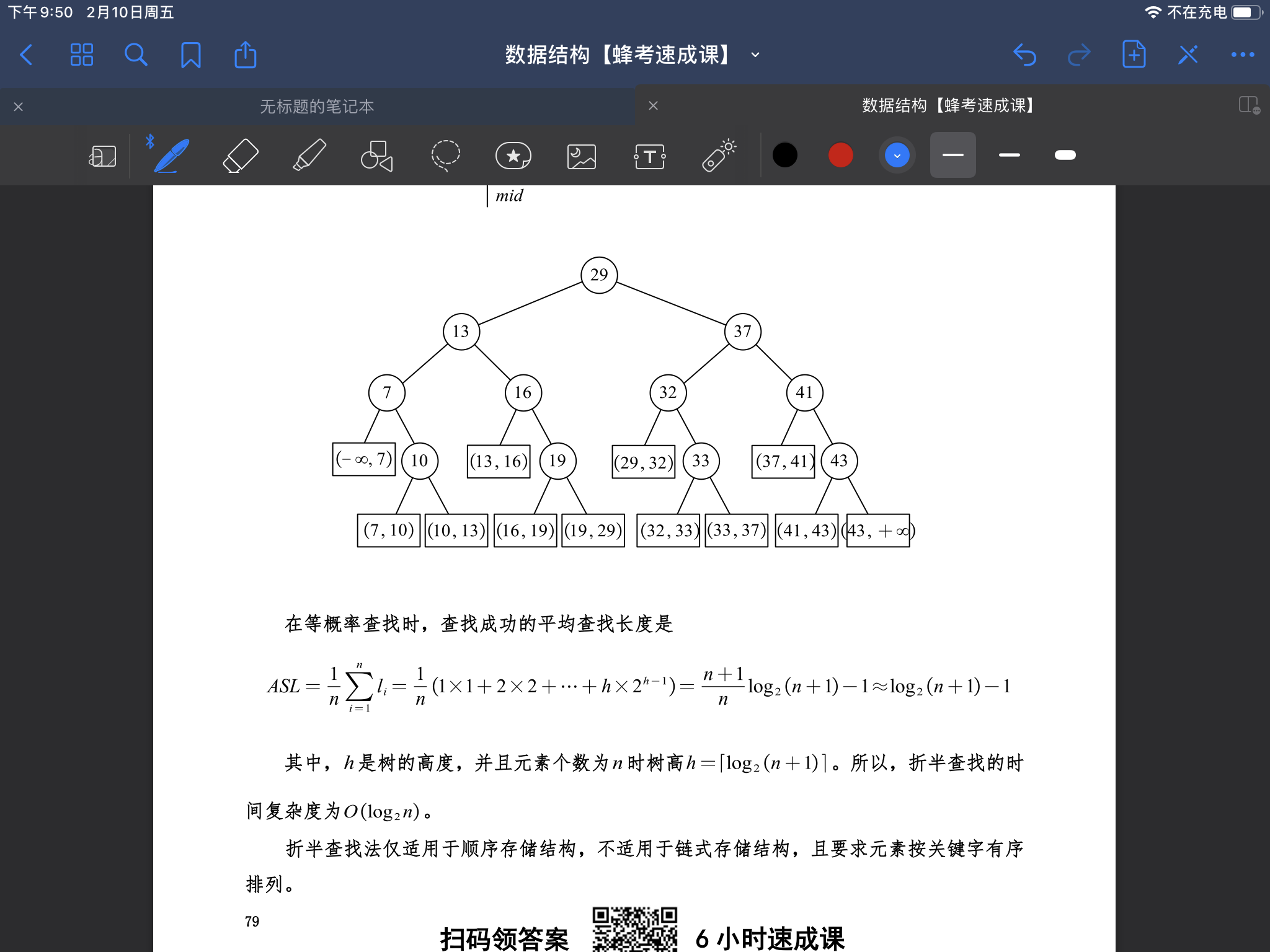
- 二叉排序树的定义
任何节点的键值一定大于其左子树中的每一个节点的键值,并小于其右子树中的每一个节点的键值。
- 掌握二叉排序树的搜索插入删除代码
搜索与插入代码:
BST_P SearchMin(BST_P root)
{
if (root == NULL)
return NULL;
if (root->lchild == NULL)
return root;
else //一直往左孩子找,直到没有左孩子的结点
return SearchMin(root->lchild);
}
BST_P SearchMax(BST_P root)
{
if (root == NULL)
return NULL;
if (root->rchild == NULL)
return root;
else //一直往右孩子找,直到没有右孩子的结点
return SearchMax(root->rchild);
}
BST_P Search_BST(BST_P root, DataType key)
{
if (root == NULL)
return NULL;
if (key > root->data) //查找右子树
return Search_BST(root->rchild, key);
else if (key < root->data) //查找左子树
return Search_BST(root->lchild, key);
else
return root;
}
void Insert_BST(BST_P *root, DataType data)
{
//初始化插入节点
BST_P p = (BST_P)malloc(sizeof(struct BST_Node));
if (!p) return;
p->data = data;
p->lchild = p->rchild = NULL;
//空树时,直接作为根节点
if (*root == NULL)
{
*root = p;
return;
}
//是否存在,已存在则返回,不插入
if (Search_BST(root, data) != NULL) return;
//进行插入,首先找到要插入的位置的父节点
BST_P tnode = NULL, troot = *root;
while (troot)
{
tnode = troot;
troot = (data < troot->data) ? troot->lchild : troot->rchild;
}
if (data < tnode->data)
tnode->lchild = p;
else
tnode->rchild = p;
}
值得一提的二叉排序树删除操作:(直接前驱/后继的意思是中序排序中的前面一个数字或者后面一个数字)
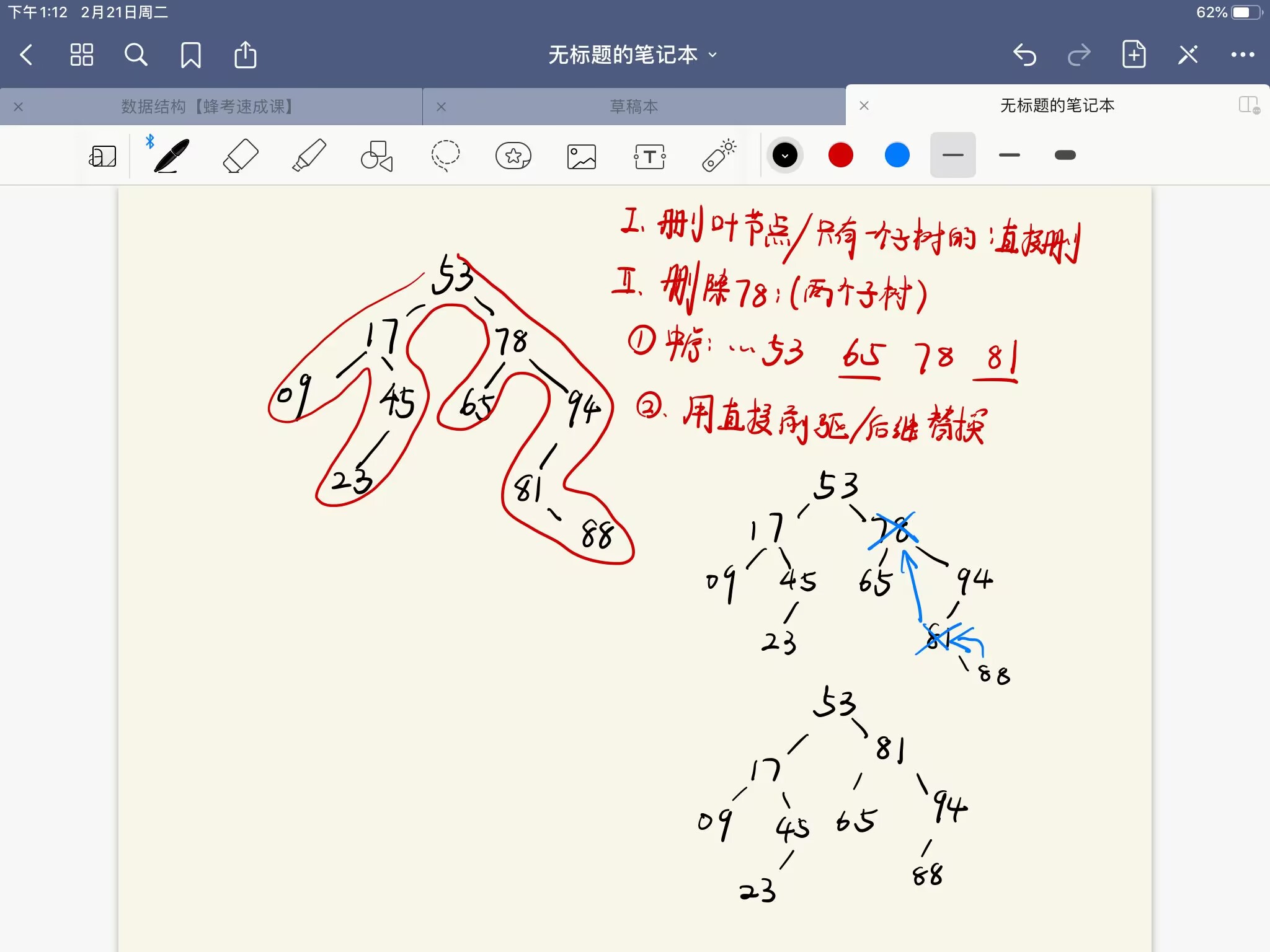
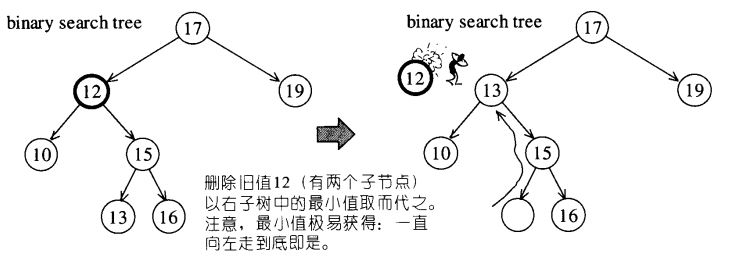
void DeleteBSTNode(BST_P *root, DataType data)
{
BST_P p = *root, parent = NULL, s = NULL;
if (!p) return;
if (p->data == data) //找到要删除的节点了
{
/* It's a leaf node */
if (!p->rchild && !p->lchild)
*root = NULL;
// 只有一个左节点
else if (!p->rchild&&p->lchild)
*root = p->lchild;
// 只有一个右节点
else if (!p->lchild&&p->rchild)
*root = p->rchild;
//左右节点都不空
else
{
s = p->rchild;
/* the s without left child */
if (!s->lchild)
s->lchild = p->lchild;
/* the s have left child */
else
{
/* find the smallest node in the left subtree of s */
while (s->lchild)
{
/* record the parent node of s */
parent = s;
s = s->lchild;
}
parent->lchild = s->rchild;
s->lchild = p->lchild;
s->rchild = p->rchild;
}
*root = s;
}
free(p);
}
else if (data > p->data) //向右找
DeleteBSTNode(&(p->rchild), data);
else if (data < p->data) //向左找
DeleteBSTNode(&(p->lchild), data);
}
- 堆up和down
void up(int x){
while(x/2 > 0 && h[x/2] > h[x]){
swap(x/2,x);
x/=2;
}
}
void down(int x){
int p = x;
//此处用临时变量:若两个子节点都小,那么用更小的替换回去
if(2*x <= idx && h[p] > h[2*x]) p = 2*x;
if(2*x + 1 <= idx && h[p] > h[2*x + 1]) p = 2*x + 1;
if(p != x){
swap(x,p);
down(p);
}
}
图论
图这一块的东西呢都代码记得很少
- 第一个理解什么是图理解什么是图以及它的逻辑结构
- 理解图的基本术语
什么是路径,什么是联通图了什么是非连通图的连通分量(连通的一部分),还有这个叫强连通图(每两点都存在路径)以及强连通分量还有生成树(顶点不变,边变少)
- 掌握图的两种存储结构邻接矩阵和邻接表
邻接表
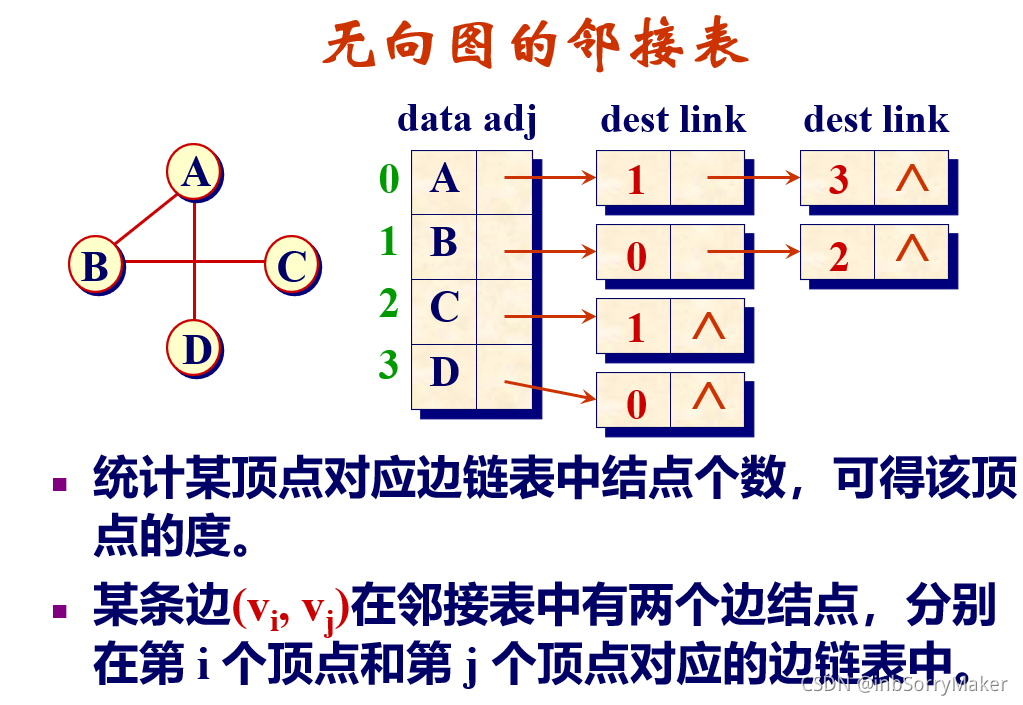
邻接矩阵
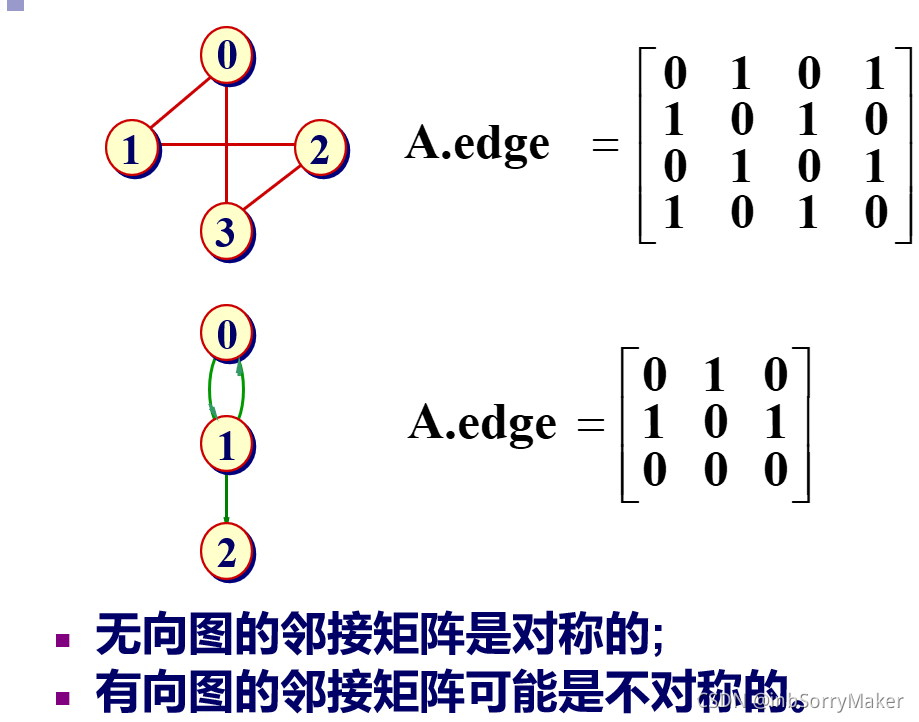
public int getFirstneighbor(int i){
for (int j=0;j<vertexNum;j++){
//顶点未访问 且 存在边
if (isVisited[j]==false && edgeMatrix[i][j]!=0){
return j;
}
}
return -1;
}
//得到结点i的下一个邻接点 j为i的上一个邻接点
public int getNextNeighbor(int i,int j){
for(int k=j+1; k<vertexNum; k++){
if (isVisited[k]==false && edgeMatrix[i][k]!=0){
return k;
}
}
return -1;
}
- 重点掌握树的深度优先遍历和广度优先遍历——非代码级
深度优先:利用栈

广度优先:利用队列
- 最小生成树算法:Prim和Kruskal,一个是顶点归并成集合,一个是边排序后归并(23年考题,考画图)
Prim算法:(On^2)
- 从源点出发,将所有与源点连接的点加入一个待处理的集合中
- 从集合中找出与源点的边中权重最小的点,从待处理的集合中移除标记为确定的点
- 将找到的点按照步骤1的方式处理
- 重复2,3步直到所有的点都被标记
Kruskal算法:O(nlogn)
- 将边按照权重从小到大排列
- 枚举第一个边,加入MST里,判断是否成环
- 如果成环则跳过,否则确定这条边为MST里的
- 继续枚举下一条边,直到所有的边都枚举完
- AOE网不看
排序
只考二分插入排序,希尔排序,冒泡排序,快速排序以及堆排序
一方面是代码,第二个是时间复杂度分析以及稳定性分析
-
排序算法复杂度大全
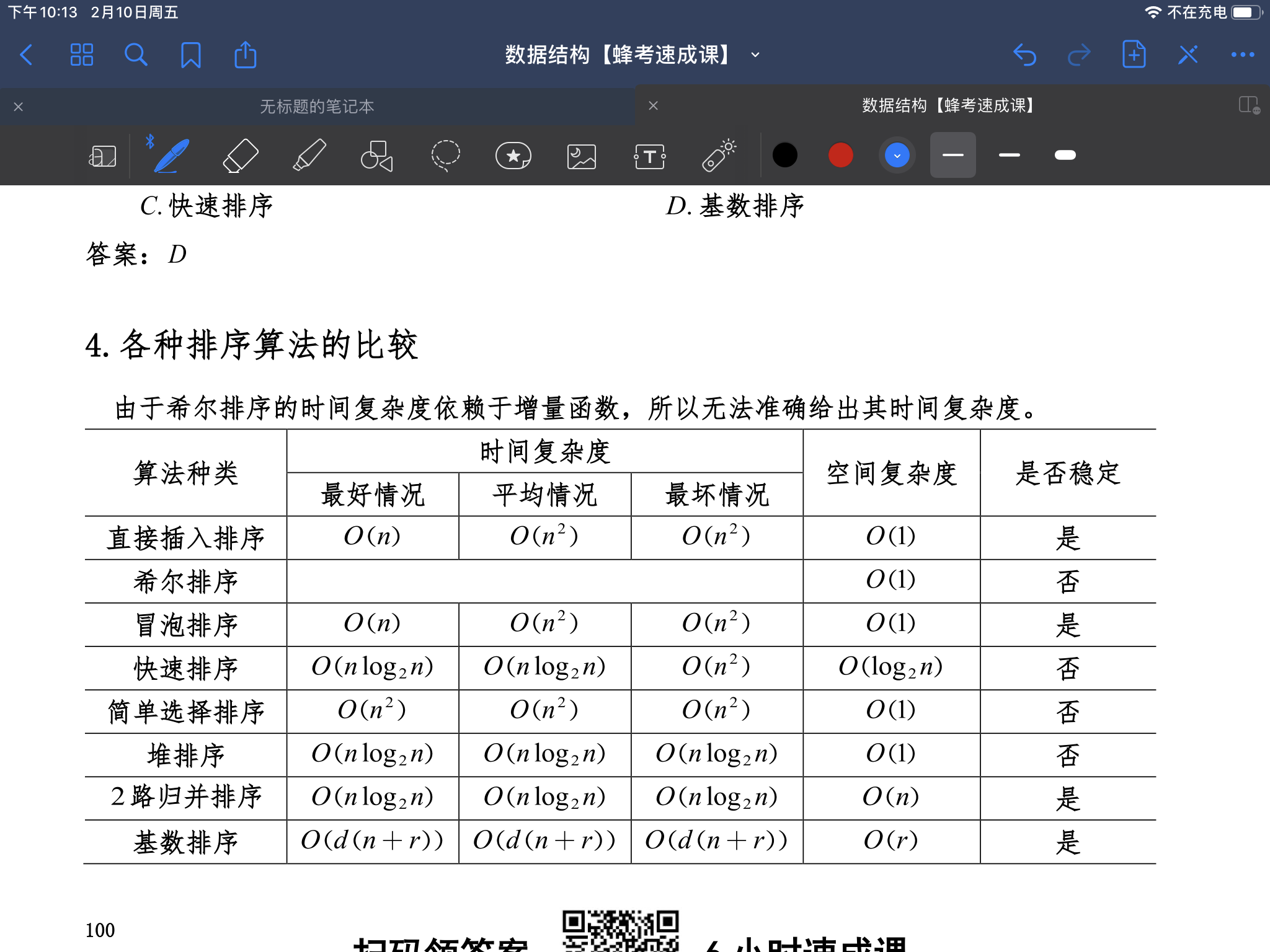
-
二分插入排序
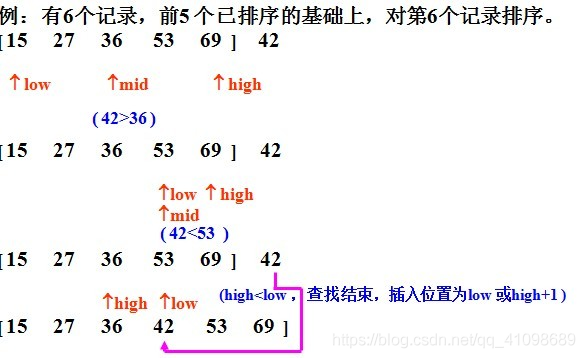
int a[]={2,45,34,324,2,3,7,555,46,34};
public void testTwoBinary(){
for(int i=0;i<a.length;i++){
int temp=a[i];
int left=0;
int right=i-1;
int mid;
//STEP1:找到插入位置
while(left<=right){
mid=(left+right)/2;
if(temp<a[mid]){
//低位
right=mid-1;
}else{
//高位
left=mid+1;
}
}
//STEP2:大于插入元素元素后移
for(int j=i-1;j>=left;j--){
a[j+1] = a[j];
}
//STEP3:插入元素 left or high + 1
a[left] = temp;
}
}
- 希尔排序
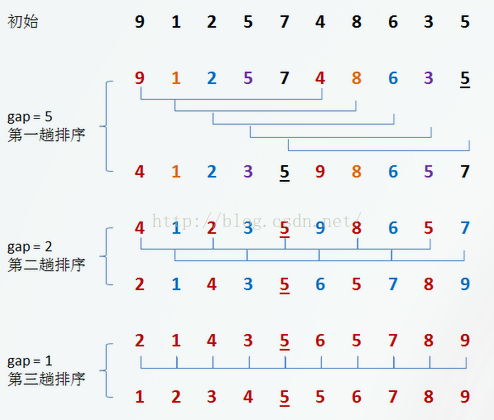
- 快速排序
https://www.bilibili.com/video/BV1XR4y1q7hT/?spm_id_from=333.337.search-card.all.click
#include <bits/stdc++.h>
using namespace std;
void bisect(int q[],int l,int r){
if(l>=r) return;
int i = l-1;
int j = r+1;
int x = q[l+r>>1];
while(i<j){
do i++; while(q[i]<x);
do j--; while(q[j]>x);
if(i < j) swap(q[i],q[j]);
}
bisect(q,l,j);
bisect(q,j+1,r);
}
int main(){
int n;
cin>>n;
int q[n];
for(int i = 0;i < n; i++){
scanf("%d",&q[i]);
}
bisect(q,0,n-1);
for(int i = 0;i < n; i++){
printf("%d ",q[i]);
}
return 0;
}
- 堆排序
思路:维护一个小根堆
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int m,n;
int a[N];
int s;
void down(int u){
int t = u;
//Watch out u and t
if(2*u <= s && a[2*u] < a[t]) t = 2*u;
if(2*u + 1 <= s && a[2*u+1] < a[t]) t = 2*u + 1;
if(u!=t){
swap(a[u],a[t]);
down(t);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
s = n;
for(int i = n/2; i ; i--) down(i);
while(m--){
cout<<a[1]<<' ';
a[1] = a[s],s--,down(1);
}
return 0;
}
23年程序题:写一个函数,判断两个节点是否是表兄弟节点:
函数模板:bool isCousin(TreeNode * root,int x,int y)
int depth(TreeNode * root){//输出给定节点的深度
if(!root) return 0;
int left = depth(root->left);
int right = depth(root->right);
return max(left,right) + 1;
}
TreeNode* GetNode(TreeNode* root,int x){//根据节点标号给出节点指针
queue<TreeNode*> q;
q.push(root);
int idx = 1;
while(!q.empty()){
q.push(root->left);
idx++;
if(q.front() == x) return q.front();
q.push(root->right);
idx++;
if(q.front() == x) return q.front();
}
}
TreeNode* parent(TreeNode* root,TreeNode*x){//找到节点x的父节点
if(root->left == x) return root;
if(root->right == x) return root;
parent(root->left,x);
parent(root->right,x);
}
bool isCousin(TreeNode * root,int x,int y){//要求构造的函数
TreeNode* tx = GetNode(root,x);
TreeNode* ty = GetNode(root,y);
if(depth(tx) != depth(ty)) return false;
if(parent(root,x) == parent(root,y)) return false;
return true;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号