基础数学拾遗

目录

• 余弦定理
• 常用泰勒展开
• 双曲线方程

---

余弦定理

对于任意一个三角形：

\[a^2 = b^2 + c^2 - 2bc * cosA \]

任意一边的平方，等于另外两边的平方和，减去2倍这两边与它们夹角余弦值的乘积。

---

常用泰勒展开

\[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... \]

\[sinx = x - \frac{x^3}{3!} + \frac{x^5}{5!} + ... \]

\[cosx = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} + ... \]

\[tanx = x + \frac{1}{3}x^3 + ... \]

\[ln(1 + x) = x - \frac{x^2}{2} + \frac{x^3}{3} + ... \]

\[\frac{1}{1 - x} = 1 + x + x^2 + x^3 + ... \]

\[\frac{1}{1 + x} = 1 - x + x^2 - x^3 + ... \]

\[(1 + x)^{\frac{1}{2}} = 1 + \frac{1}{2}x + ... \]

\[(1 + x)^α = 1 + αx + \frac{α(α - 1)}{2}x^2 + ... \]

\[arctanx = x - \frac{1}{3} x ^ 3 + \frac{1}{5}x^5 + ... \]

\[arcsinx = x + \frac{x^3}{6} + ... \]

---

双曲线方程

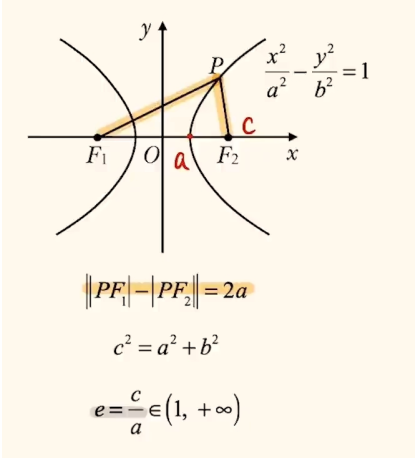
被减数是哪个，哪个就是纵轴。

点\((x_0, y_0)\)在双曲线上切线方程：

\[\frac{x_0x}{a^2}-\frac{y_0y}{b^2} = 1 \]