对公众号算法题的补充和思考

（其实就是因为公众号不能修改文章内容，现在也没有留言功能，所以才专门写篇文章来进行补充，我会利用好标题的索引功能，方便大家快速查找到想要看的题目；至于为什么用公众号发算法题题解，主要是个人感觉公众号的排版会好看点）

【AcWing】2.01背包

原文链接：https://mp.weixin.qq.com/s/ijWXxAAH-mC_hOP_iGPreg

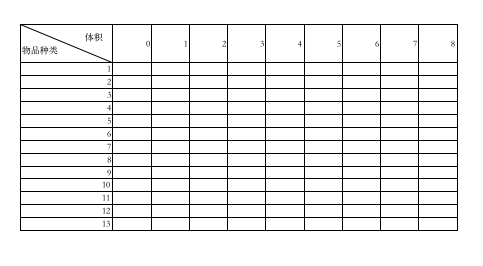
为什么要双重循环？

是为了将每种可能出现的情况都罗列出来。比如：选一个物品的时候，体积为0会怎么样，体积为1会怎么样，以此类推。

注意，leetcode是要return，acwing是要cout，每种机制不一样，要看清题意，看清是哪种机制。在AcWing中如果没有cout而是return的话，就会显示以下错误：Non Zero Exit Code

【AcWing】9.分组背包问题

原文链接：https://mp.weixin.qq.com/s/Sa_qvHRgStkawDvfQ6Wcqg

1、分组背包：状态计算时，画的那个椭圆，表示要从第 i 组背包中选出一个物品，可以不选，选第1个，第2个，……第k个。

　　　　　　在进行 f[i][j] 之前，也就是在开始从这个椭圆中选择某个物品之前，已经完成的状态是选好了前（i-1）组背包里面需要的东西，即满足f[i-1][ ]。

2、分析好每重循环的含义：第一重for循环表示遍历从第 i 组背包中选

　　　　　　　　　　　　第二重for循环表示遍历体积

　　　　　　　　　　　　第三重for循环表示遍历上面状态计算那个椭圆，在满足了f[i-1][ ]的情况下，要达到f[i][ ]，就需要再往前走一步，也就是从第 i 组物品中选一个物品

3、多重背包可以看做是分组背包的特殊情况，把分组背包里面每一组都变成一样的物品，就是多重背包里面的每种物品，只不过有点不一样的是，分组背包每组（种）只能选1个，多重背包每种（组）可以选多个。

4、因为从第几个物品组里面选一个物品的时候，要能够到具体到里面的第几个物品，所以要用二维数组来确定一个物品的体积和价值。

5、多重背包每种（组）可以选多个，那是多少个？所以才有了第三重循环，去看看要选多少个此物品

　　分组背包每组（种）只能选1个，那到底是哪一个？所以才有了第三重循环，去看看选本组里面的第几个物品

6、总结：其实背包问题就有点像在教室里面，有多个小组，从每个组里面选动物，一种物品可以看成是一个小组。

　　　　 01背包：对于面前的每个小组，要么选一个，要么不选。

　　　　多重背包：对于面前的每个小组，同一组内里面每只动物种类都是一样的，比如第1组都是狗，相当于第1种物品。可以从每组里面选0~全部，只要不超过体积j就行。

　　　　完全背包：第一句同多重背包一样，只不过有个不同点，就是可以从每组里面选0~无穷多个，只要不超过体积j就行。

　　　　分组背包：对于面前的每个小组，同一组内有不同种类的动物，每个种类的动物有且仅有一只，并且每组最多只能选一只动物，只要不超过体积j就行。　　　

7、相类似的题目：https://www.luogu.com.cn/problem/P1757

#include<iostream>
using namespace std;

const int N = 110;

int n, m;
int f[N][N], v[N][N], w[N][N], s[N];

int main(){
    cin >> n >> m;

    for(int i = 1; i <= n; ++ i){  // 有多少组物品
        cin>> s[i];
        for(int j = 1; j <= s[i]; ++ j) { // 每组物品有多少个
            cin >> v[i][j] >> w[i][j];
        }
    }

    for (int i = 1; i <= n; ++ i)   // 枚举第i个物品组
        for (int j = 0; j <= m; ++ j)   // 从大到小枚举体积
            for (int k = 0; k <= s[i]; ++ k)    
                if (v[i][k] <= j) 
                    f[i][j] = max(f[i][j], f[i-1][j - v[i][k]] + w[i][k]);  
                    // 不用专门去写f[i-1][j]，因为当k = 0的时候，就是f[i-1][j]，已经把它算进去了

    cout<< f[n][m] <<endl;
    return 0;
}

公众号上朴素写法失误贴上了优化做法的图，在这里补充一下本题朴素做法

【ACWing】830.单调栈

原文链接：https://mp.weixin.qq.com/s/f2gf1u2tSRD1Hv4HDwYr6A

y总的图解：https://tva1.sinaimg.cn/large/e6c9d24ely1h6gpv9dad3j20wx0frjs4

　　https://tva1.sinaimg.cn/large/e6c9d24egy1h6gq5mezpvj20p80fawet

a[i] 前面的那些比它大的，都被弹出栈中了，最终 a[i] 前面的数是找到的“左边第一个比它小的数”，按照这样的逻辑下去，那么最后整个栈内元素必将是严格递增的。

举个例子，你可以假设找a[2]前面的比它小的数，找得到就继续往下，找不到将 a[1] 弹出。也就是说每个 a[ ] 前面比它大的数，都得被弹出，都删掉，所以最后整个栈内元素必将是单调递增的。

for循环的含义：为了找到每个数对应的「左边第一个最小值」，遍历每个数

while循环里面的st[ ]，中括号里面放的应该是tt，表示取栈顶元素。

总体的思路：一个数输入后，看能不能找到「左边第一个最小值」，找到了，就输出出来，然后把自己入栈，因为它自己有可能会成为后面其它数想要的结果。

至于st[++t] = x为什么要++t ？

t指向栈顶的位置，栈顶是从索引1开始的，st[0]的时候，没有存入x，这样的话，t的大小就表示了栈中的元素个数

从程序刚开始的角度看，while(t && st[i] >= x)意思是：因为t的大小表示了栈中的元素个数，这样就能够巧妙了利用了t=0让while不能执行循环的特性，如果栈中没有元素（t=0时），就不用找了（即不用执行while循环），if(t)也不用输出了，直接入栈一个先。

从运行到中间的角度看，while(t && st[i] >= x)意思是：弹出的t的值是找到的目标的下标索引，那就输出st[t]，表示找到了某个数「左边第一个最小值」，后面st[++t] = x则表示找到了「左边第一个最小值」之后，就把中间那些不用的弹出，把刚刚那个找「左边第一个最小值」的 x 给录入进去，因为后面的数的目标是有可能是x的，也就是说后面的数是有可能比x小的。

【ACWing】831.KMP字符串

原文链接：https://mp.weixin.qq.com/s/QNB2QsZVos0aLJ4yje9jKw

1、问：关于第二个for循环里面cout << i - n << " ";这一步怎么理解好呢？

答：题目要求的是要找到「匹配成功位置的初始下标」，那么知道匹配成功的长度是n，那就是往前移动n位！

为什么这么说？这其实跟题目默认要求输出的「下标是以0开始的数组」有关系。

那假设n = 1，匹配成功的长度1，我们的代码写法是「从下标1开始的」，所以匹配到的时候，本来是输出i，但是由于要考虑题目的默认要求（输出结果下标索引默认是从0开始的），所以i-1，往前移动一位；

假设n = 2，i向前移动1位就到了「匹配成功位置的初始下标」，但是考虑到题目默认要求，所以得输出i-2

假设n = 3，i向前移动2位就到了「匹配成功位置的初始下标」，但是考虑到题目默认要求，所以得输出i-3

以此类推，最后应该输出i-n

【AcWing】844.走迷宫

 while(q.size()) {
        PII t = q.front();
        q.pop();
        
        for(int i = 0; i < 4; ++i) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if(x > 0 && x <=n && y > 0 && y <= m && d[x][y] == -1 && g[x][y] == 0) {
                d[x][y] = d[t.first][t.second] + 1;
                q.push({x, y});
            }
        }
        
    }

if里面在判断下一个位置是否合法时，注意一个条件就是g[x][y] == 0,题目要求，0才能够走

类似题目：移动骑士

移动骑士题解：https://www.acwing.com/solution/content/141498/

　　　　　　　https://www.acwing.com/solution/content/64323/

int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};

这里没有规定说，一定要按哪个顺序去走，所以上下左右可以随便走，没有固定顺序

【AcWing】896. 最长上升子序列

1、本题为什么要用res来max一下？最长公共子序列那题就不用？最长公共子序列就直接f[n][m]？

有可能前面就上升完了，就前面可能上升的那一段就可能是最长的那段了，后面的那段可能还没那么长，所以要用res记录一下每段上升子序列的长度，max一下取最长。

最长公共子序列那题的话，就是假设全部相等的话，两个字符串给的字符越多，相等的就越多，公共子序列就越长，所以在把两边所有的字符都考虑进去后，得到的结果f[n][m]就是两个字符串的最长公共子序列了。

【AcWing】896. 最长上升子序列 II

原文链接：https://mp.weixin.qq.com/s?__biz=Mzg3OTc2NzM0MA==&amp

1、问：while(l < r)的时候，最后弹出来的结果 f[l] （或者说 f[r] ），跟 a[i] 相比有三种可能是吗？等于是有可能的，那小于和大于呢？

　答：假设只有两个数4、8

1⃣ 如果要插入的是3呢？那是不是在原来4的位置，比4小。
2⃣ 如果要插入的是5呢？那是不是在原来4的位置，比4大。

⭐️ 综上，当while(l < r)的最后 l = r的时候，不论跟 a[i] 的大小关系如何，就是所要的答案，就是所要插入替换的位置！！

【Leetcode】410.分割数组的最大值

1、大家可以参考一下这篇题解，跟我写的有点不一样，但写的挺好的。

https://leetcode.cn/problems/split-array-largest-sum/solution/er-fen-cha-zhao-by-liweiwei1419-4/

2、忘记说了，这道题是一道很经典的二分查找的例题，最大值最小化。

如何理解最大值最小化和最小值最大化的文章：https://blog.csdn.net/yxnd150150/article/details/53391202

最大值最小化是上面链接文章中的（一）👆🏻，最小值最大化则是（二）。

3、个人理解：其实整个过程就是在预测，调整，预测，调整，跟机器学习做的事某种程度上有点像（可能有偏差，勿喷）。

4、红色框那里不能放等于号！！！

如果超过了，就不能够算在本次划分的块内，但是如果刚好等于的话，是算在本次的块内的，所以应该包含到sum+=x里面，如果包含到这里的话，sum=x，让这个数重新开始，就不对了。

至于什么时候需要等号，什么时候不需要等号，要看具体的题意。

5、下图来自《算法竞赛入门经典》

6、类似题目： http://poj.org/problem?id=2456

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e5 + 10;

int n, m, a[N];

bool check(int a[],  int mid) {     // 如果按照mid这个标准来划分，容纳下的牛的数量大于实际牛的数量m，就返回true，然后用二分去把mid调大
   int cnt = 1;     // 至少可以容下一头牛
   int cur = 0, next = 1;       // cur 表示当前已经使用的房子编号，next表示下一个将要使用的房子编号

   while(next < n) {
       if(a[next] - a[cur] >= mid) {
           cnt++;
           cur = next;
       }
       next++;
   }

   if (cnt >= m) return true;
   return false;
}

int main() {
   cin >> n >> m;
   int t = 0;
   for(int i = 0; i < n; ++i)  {
      cin >> a[i];
    }
   sort(a, a + n);  // 要理清楚a[]里面每个数字的含义，它的意思是，每个数字是相当于放在x轴上，相对于原点（0,0）的距离，排好序之后，才好求相邻两个房子间的距离，因为第一间和第二间可能不相邻，不要问为什么，题目的意思是单纯把第几间看成是一个标号而已，你可以随意改变，排好序后，就是真正意义上的第一间和第二间相邻了，因为排序可能会把数字对应的下标索引也改变

   int low = 0, high = INT_MAX;      // 这里仍然可以这么取，是没有关系的，反正一直缩减范围

   while (low < high) {
      int mid = (high+low+1)>> 1;
      if (check(a, mid)) {
         low = mid;     // return true，就是在取mid的时候，是有可能取刚好取到所要的值的，即刚好等于m牛的数量的
                        // low缩减，是因为取的cnt太多，把划分标准提高一下，即让mid提高一下
      } else {
         high = mid - 1;
      }
   }
      cout << high;

      return 0;
}

2456题答案

这篇文章的代码答案好像不正确，但是思路可以借鉴一下：https://blog.csdn.net/Eas_on/article/details/102727296

7、类似题目：https://www.nowcoder.com/questionTerminal/30cff18caa434dee98b6f0b8200bfdd2?f=discussion&toCommentId=14613768

如果按这个mid为标准去划分的话，反向算出需要多少个x（记为cnt）才能够将整体水平的最大值降到mid，也就是说有可能a[ ]全部都要减x，减多少个不知道，就是有这个可能性。

所以check函数是代表什么意思？

意思就是，按照mid这个标准去划分，判断算出来的cnt是不是等于k，或者说是偏大还是偏小。就是让cnt跟k进行比较，看是比k多还是比k少，然后才可以对【left，right】范围进行缩减。（cnt是等于k的话，该怎么做，是偏大or偏小该怎么做，main函数的二分查找里面都有写）

mid值放进check里面后
check函数说：你这个值啊，太小了！！你看看你，需要这么多个x，才让整体每个值都小于或等于你，你这样怎么做大王啊！？我要的是你用k个x就给我解决了“让所有人都比你小”这件事，但是你却没有做到，你你你……，不要你了，来个大一点的，才不用浪费那么多个x，我浪费k个刚刚好就行啊！不要多，不要少！！！！

a[i] - mid，然后再除以x，就是算出被减了多少个x，k个指的是x有k个，那这里算出来被减了多少个x，然后再跟k去比较，如果比k多，那就是mid小了，因为这样的话，a[i]-mid就大了，除以k后得到的份数就多了。那mid就得扩大，故 l = mid + 1。

mid是预测的答案值，是变小后的最大值。如果原来a[ ]中有比变小后的最大值还大的，那它一定会经历一个变小的过程，成为一个小于等于最大值的值。

((a[i]-mid)%x > 0 ? 1: 0)是指，如果前面减了之后，仍然有剩余，也就是不能让这个a[i]小于最大值，那就多来一个x，让其小于最大值。

for循环对cnt进行叠加，看看把这群a[ ]全部降到最大值以下需要多少个x。

【牛客网】冒泡排序

原文链接：https://mp.weixin.qq.com/s/0bAr8NMt0WGEcIj47YtGRQ

关于for循环里面第二层的含义：需要交换（n-每轮不用考虑的数的个数）次

当下标索引为0的时候，i = 0，第1轮「不需要考虑的数的个数」为0个，需要交换的次数是n-1，即n -（i+1）

　　　　　　　　　　 i = 1，第2轮「不需要考虑的数的个数」为1个，需要交换的次数是n-2，即n - （i+1）

　　　　　　　　　　 i = 2，第3轮「不需要考虑的数的个数」为2个，需要交换的次数是n-3，即n - （i+1）

　　　　　　　　　　 i = 3，第4轮「不需要考虑的数的个数」为2个，需要交换的次数是n-4，即n - （i+1）

　　　　　　　　　　以此类推，需要交换n-（i+1）次

当下标索引为1的时候，i = 1，第1轮「不需要考虑的数的个数」为0个，需要交换的次数是n-1，即n -i

　　　　　　　　　　 i = 2，第2轮「不需要考虑的数的个数」为1个，需要交换的次数是n-2，即n -i

　　　　　　　　　　 i = 3，第3轮「不需要考虑的数的个数」为2个，需要交换的次数是n-3，即n -i

　　　　　　　　　 i = 4，第4轮「不需要考虑的数的个数」为3个，需要交换的次数是n-4，即n -i