泰勒级数

泰勒级数的重大意义，即在于“它使单变量函数(只有一个自变量x的函数)可以展成幂级数的形式”，然后再处理计算。这对解决“复杂函数”具有重要意义。将复杂函数“化成”幂函数的连加形式，即幂级数形式，由于人们对处理幂函数很有经验，所以这样一来，本来没法处理的“非初等函数”的“复杂函数”，就可以处理计算了。
泰勒原以为他的发现适用于一切单变量函数，但后来证明不行。
泰勒之后，麦克劳林、拉格朗日、柯西发展完善了泰勒公式。拉格朗日认识到了这公式的重要性（以前没认识到）；而公式的严谨证明由柯西于十九世纪二十年代最终完成。

 

 

在数学上，一个在实数或复数a邻域上的无穷可微实变函数或复变函数ƒ(x)的泰勒级数是如下的幂级数：

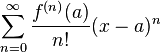
\sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}

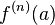这里，n! 表示n的阶乘而f^{(n)}(a)\,\!表示函数f在点a处的n阶导数。如果a = 0，那么这个级数也可以被称为麦克劳伦级数。

泰勒级数列表[编辑]

在复平面上余弦函数的实数部分。
在复平面上余弦函数的第八度逼近
两个以上的曲线放在一起

下面我们给出了几个重要的泰勒级数。参数x 为复数时它们依然成立。

\frac{1}{1-x} = \sum^{\infin}_{n=0} x^n\quad \forall x: \left| x \right| < 1
(1+x)^\alpha = \sum^{\infin}_{n=0} C(\alpha,n) x^n\quad \forall x: \left| x \right| < 1, \forall \alpha \in \mathbb{C}
二项式展开中的C(α,n)是二项式系数。
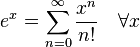
e^{x} = \sum^{\infin}_{n=0} \frac{x^n}{n!}\quad \forall x
\ln(1+x) = \sum^{\infin}_{n=1} \frac{(-1)^{n+1}}n x^n\quad \forall x\in (-1,1]
\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\quad \forall x
\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}\quad \forall x
\tan x = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}\quad \forall x: \left| x \right| < \frac{\pi}{2}
\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n}\quad \forall x: \left| x \right| < \frac{\pi}{2}
\arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad \forall x: \left| x \right| < 1
\arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1}\quad \forall x: \left| x \right| < 1
\arctan x = {{\pi {\mathop{\rm sgn}} x} \over 2} - {1 \over x} + \sum_{k = 1}^\infty {{{\left( { - 1} \right)^k } \over {\left( {2k + 1} \right)x^{2k + 1} }}} \quad \forall x: \left| x \right| > 1
tan(x)展开式中的Bk是伯努利数。sec(x)展开式中的Ek是欧拉数。
\sinh x = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1}\quad \forall x
\cosh x = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n}\quad \forall x
\tanh x = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1}\quad \forall x: \left| x \right| < \frac{\pi}{2}
\sinh^{-1} x = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad \forall x: \left| x \right| < 1
\tanh^{-1} x = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1}\quad \forall x: \left| x \right| < 1
tanh(x)展开式中的Bk是伯努利数。
W_0(x) = \sum^{\infin}_{n=1} \frac{(-n)^{n-1}}{n!} x^n\quad \forall x: \left| x \right| < \frac{1}{e}

posted on 2014-07-24 16:54  alexanderkun  阅读(1214)  评论(0)    收藏  举报

导航