图论 II

图论 I

Luogu & cnblogs

1. 2-SAT

前置知识：强连通分量。

2-SAT 是布尔代数领域的经典问题。为了更好地理解相关算法，读者需要掌握一些基本的逻辑概念。

1.1 相关定义

• 合取：合取就是逻辑与 &&，记为 \(\land\)。\(p\land q\) 表示 \(p, q\) 的合取，称为合取式，表达式为真当且仅当 \(p, q\) 均为真。
• 析取：析取就是逻辑或 ||，记为 \(\lor\)。\(p\lor q\) 表示 \(p, q\) 的析取，称为析取式，表达式为真当且仅当 \(p, q\) 至少一个为真。
• 否定：否定就是逻辑非 !，记为 \(\lnot\)。\(\lnot p\) 表示 \(p\) 的否定，其真假性与 \(p\) 相反。

如何记忆符号才不会混淆呢？\(\land\) 看成集合求交 \(\cap\)，只有两者都是 \(1\) 最终才是 \(1\)，\(\lor\) 看成集合求并 \(\cup\)，两者只要有 \(1\) 最终就是 \(1\)。

• 布尔逻辑式：将命题变元（要么真要么假的布尔变量）用合取 \(\land\)，析取 \(\lor\) 和否定 \(\lnot\) 联结在一起，就是 布尔逻辑式。
• 布尔逻辑式 可满足，当且仅当存在一个对所有命题变元的真假赋值，使得该布尔逻辑式为真。例如，逻辑式 \((p_1\lor \neg p_2) \land (\neg p_1\lor p_2\lor p_3) \land \neg p_1\) 是可满足的：令 \(p_1 = \mathrm{False}\)，\(p_2 = \mathrm{False}\)，\(p_3\) 任取。但逻辑式 \(p\land \neg p\) 是不可满足的。
• SAT：检查一个布尔逻辑式是否可满足称为 布尔可满足性问题，简称 SAT。

为了解决 SAT，我们希望把任意布尔逻辑式转化为标准形式，比如说外层合取内层析取的 \((a\lor b)\land (c\lor d)\)，或者是外层析取内层合取的 \((a \land b) \lor (c\land d)\)。根据基本的逻辑知识，这是一定可以做到的。

• 双重否定：\(\neg \neg p = p\)。
• 结合：\((p \lor q) \lor r = p \lor (q \lor r)\)，\((p \land q) \land r = p \land (q \land r)\)。
• 交换：\(p\lor q = q\lor p\)，\(p\land q = q\land p\)。
• 分配：\(p\land (q\lor r) = (p\land q) \lor (p\land r)\)，\(p \lor (q\land r) = (p\lor q) \land (p\lor r)\)。
• 反演：\(\neg(p\land q) = \neg p\lor \neg q\)，\(\neg (p\lor q) = \neg p \land \neg q\)。

以上的 \(p\) 和 \(q\) 也可以是布尔逻辑式。

首先根据反演律，将所有逻辑非下放到命题变元的前面。再根据双重否定律让每个命题变元前面的逻辑非的个数不超过 \(1\)。最后根据分配律，将所有析取下放到最底层，例如 \((a \land b) \lor (c \land d) = (a\lor c)\land (a\lor d) \land (b\lor c) \land (b\lor d)\)，过程中不断使用结合律去掉括号。这样就得到了布尔逻辑式的外层析取内层合取的等价形式。

• 命题变元或其否定称为 文字。在布尔逻辑式中，一个命题变元 \(p\) 可以以 \(p\) 和 \(\lnot p\) 的形式出现多次，每次出现都是一个文字，这些文字的真假由 \(p\) 的真假确定。
• 若干文字的析取称为 简单析取式，形如 \(P = x_1 \lor x_2 \lor \cdots \lor x_k\)，其中 \(x_i\) 表示命题 \(p_j\) 或其否定 \(\lnot p_j\)。
• 若干简单析取式的合取称为 合取范式 (conjunctive normal form, CNF)，形如 \(P_1 \land P_2 \land \cdots \land P_n\)，其中 \(P_i\) 表示简单析取式。

类似定义简单合取式与析取范式。根据上述分析，任意布尔逻辑式均可转化为合取范式和析取范式。

检查合取范式是否可满足的问题称为 k-SAT，其中组成它的每个简单析取式至多含有 \(k\) 个文字。当 \(k\geq 3\) 时 k-SAT 是 NPC 问题（第一个被证明的 NPC 问题），而 2-SAT 存在多项式复杂度的解法。

1.2 算法介绍

考虑一个合取范式。外层的合取要求内层的每个简单析取式都要为真。简单析取式只有五种形态：\(p_i\)，\(\lnot p_i\)，\(p_i\lor p_j\)，\(p_i \lor \lnot p_j\)，\(\lnot p_i \lor\lnot p_j\)，因为至多含有两个文字。以 \(p_i\lor \lnot p_j\) 为例，此时 \((p_i, p_j)\) 的取值不能是 \((0, 1)\)，这个限制可以用两个限制描述：“如果 \(p_i = 0\)，那么 \(p_j = 0\)”，以及 “如果 \(p_j = 1\)，那么 \(p_i = 1\)”。

这样表示有什么好处呢？注意到若 \(A\) 则 \(B\) 的逻辑是具有传递性的：若 \(A\) 则 \(B\)，若 \(B\) 则 \(C\)，那么若 \(A\) 则 \(C\)。这启发我们往图论方向上思考。根据逻辑建图是一种常用的解题方法，因为可达具有传递性，而蕴含同样具有传递性。根据这些若则的限制，我们建出一张有向图，它准确地表示了当每个文字为真时，有哪些文字必须为真。

具体地，对于每个命题 \(p_i\)，我们在图上加入两个点 \(p_i\) 和 \(\lnot p_i\) 分别表示 \(p_i = 1\) 和 \(p_i = 0\)。考虑每个简单析取式产生的限制。

• 形如 \(p_i\)：\(p_i\) 必须为真。用若 \(\neg p_i\) 则 \(p_i\) 限制 \(p_i\) 为真。
• 形如 \(\neg p_i\)：\(p_i\) 必须为假。用若 \(p_i\) 则 \(\neg p_i\) 限制 \(p_i\) 为假。
• 形如 \(p_i\lor p_j\)：\(p_i\) 和 \(p_j\) 不能同时为假。因此，若 \(\neg p_i\) 则 \(p_j\)，若 \(\neg p_j\) 则 \(p_i\)。
• 形如 \(p_i\lor \neg p_j\)：若 \(\neg p_i\) 则 \(\neg p_j\)，若 \(p_j\) 则 \(p_i\)。
• 形如 \(\neg p_i\lor \neg p_j\)：若 \(p_i\) 则 \(\neg p_j\)，若 \(p_j\) 则 \(\neg p_i\)。

特别地，第三、四、五条的连边具有对称性，因为若一个命题成立，则其逆否命题成立：若 \(A\implies B\)，则 \(\neg B\implies \neg A\)。这一点很重要。

这样，若命题 \(p_i\) 为真推导出其否定为真，即 \(p_i\rightsquigarrow \neg p_i\)，则命题必须为假。类似地，若 \(\neg p_i\rightsquigarrow p_i\)，则命题必须为真。进一步地，若 \(p_i\) 和 \(\neg p_i\) 对应的点强连通，则 2-SAT 无解。对有向图进行 SCC 缩点，若 \(p_i\) 和 \(\neg p_i\) 在同一强连通分量，说明 \(p_i\) 必须真且必须假，无解。除此以外是否一定有解呢？

首先确定解的形态。对于命题 \(p_i\) 相关的两个文字 \(p_i\) 和 \(\neg p_i\)，有且仅有一个文字为真，对应 \(p_i\) 为真或假。所有为真的共 \(n\) 个文字对应的点集 \(P\)，在有向图上可达的点不能同时包含一个命题及其否定。这说明 \(P\) 可达的点数恰好为 \(n\)，继而得到 \(P\) 只可达 \(P\) 本身（\(P\) 是闭合子图），等价表述为不存在一个假文字被真文字到达。

接下来尝试构造一组解。注意到若 \(\neg p_i\rightsquigarrow p_i\)，则 \(p_i\) 的拓扑序大于 \(\neg p_i\)。所以我们猜测，对每个命题及其否定，选择拓扑序较大的文字为真是可行的。

证明

反证法。假设存在 \(p_i, p_j\) 满足 \(p_i\) 的拓扑序大于 \(\lnot p_i\)，\(p_j\) 的拓扑序大于 \(\lnot p_j\)，但是 \(p_i\) 可达 \(\lnot p_j\)（某个被选文字的否定形式由另一个被选文字可达是方案不合法的唯一情况），则 \(\neg p_j\) 的拓扑序大于 \(p_i\)。根据命题与其逆否命题的等价性，\(p_j\) 可达 \(\lnot p_i\)，则 \(\neg p_i\) 的拓扑序大于 \(p_j\)。

可得拓扑序关系：\(p_i > \neg p_i > p_j > \neg p_j > p_i\)，矛盾。\(\square\)

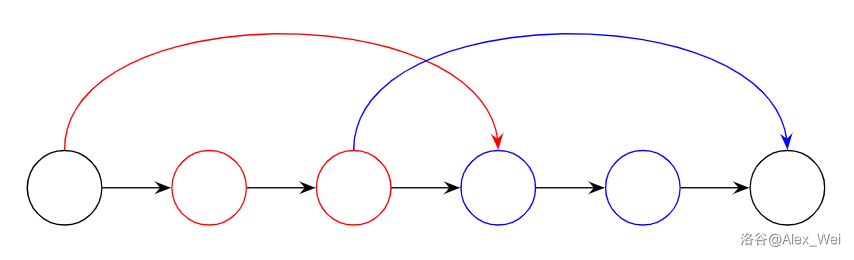
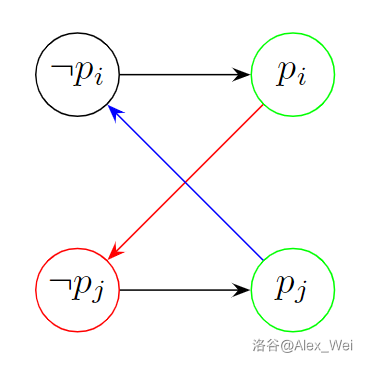
一个最简单的例子是上图。绿色是我们选择的点。如果红色边存在，那么红色点和绿色点将导致方案不合法。但根据对称性，一定存在蓝色边，于是 \(\lnot p_i\) 和 \(p_i\) 在同一个强连通分量，和有解矛盾。

在缩点后的图上拓扑排序。对每个命题相关的两个文字，选择拓扑序较大的为真。因为在 Tarjan 缩点时已经得到了 DAG 的反向拓扑序，只需选择所在 SCC 编号较小的文字赋为真即可。时间复杂度 \(\mathcal{O}(n + m)\)，其中 \(n\) 是命题数，\(m\) 是析取式数量，即限制数。注意开两倍空间。

若要求字典序最值解，可以按位贪心，并检查当前决策是否出现矛盾（一个命题对应的两个文字均由已选择的文字可达）。贪心的局部决策不影响全局合法性，证明是类似的。时间复杂度 \(\mathcal{O}(n(n + m))\)。Bitset 优化求传递闭包可做到 \(\mathcal{O}(\frac{n ^ 3} w)\)。

模板题 代码。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e6 + 5; // 两倍空间
int cnt, hd[N], nxt[N], to[N];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}
int n, m, dn, dfn[N], low[N], top, stc[N], vis[N], cn, col[N];
void tarjan(int id) {
  dfn[id] = low[id] = ++dn, vis[id] = 1, stc[++top] = id;
  for(int i = hd[id]; i; i = nxt[i]) {
    int it = to[i];
    if(!dfn[it]) tarjan(it), low[id] = min(low[id], low[it]);
    else if(vis[it]) low[id] = min(low[id], dfn[it]);
  }
  if(low[id] == dfn[id]) {
    col[id] = ++cn;
    while(stc[top] != id) col[stc[top]] = cn, vis[stc[top--]] = 0;
    vis[id] = 0, top--;
  }
}
int main() {
  cin >> n >> m;
  for(int i = 1; i <= m; i++) {
    int u, a, v, b;
    scanf("%d%d%d%d", &u, &a, &v, &b);
    add(u + (!a) * n, v + b * n); // 当 u 等于 !a 时，v 必须等于 b
    add(v + (!b) * n, u + a * n);
  }
  for(int i = 1; i <= n * 2; i++) if(!dfn[i]) tarjan(i);
  for(int i = 1; i <= n; i++) if(col[i] == col[i + n]) puts("IMPOSSIBLE"), exit(0);
  puts("POSSIBLE");
  for(int i = 1; i <= n; i++) putchar('0' + (col[i + n] < col[i])), putchar(' '); // 选 col 较小的
  return 0;
}

1.3 例题

P3825 [NOI2017] 游戏

如果没有 x 就是裸的 2-SAT。

注意到 \(d\) 非常小，所以 \(2 ^ d\) 枚举每个 x 的状态：a 或 c，这保证了任何一种合法解都被考虑到。

时间复杂度 \(\mathcal{O}(2 ^ d(n + m))\)。代码。

*P6965 [NEERC2016] Binary Code

一个字符串至多含有一个问号，所以状态至多有两种，考虑 2-SAT，设 \(x_i\) 表示第 \(i\) 个字符串的问号填 \(0\)，\(\lnot x_i\) 表示第 \(i\) 个字符串的问号填 \(1\)。现在我们有 \(2n\) 个字符串和 \(2n\) 个文字，它们之间一一对应。

容易发现，若字符串 \(s\) 是 \(t\) 的前缀，则若 \(s\) 对应文字为真，则 \(t\) 对应文字为假；若 \(t\) 对应文字为真，则 \(s\) 对应文字为假。这说明若 \(s\) 则非 \(t\)，若 \(t\) 则非 \(s\)。

刻画前缀关系的结构是字典树。对于若 \(s\) 则非 \(t\) 的限制，我们需要从 \(s\) 向它的子树内所有字符串的 否定 连边。对于若 \(t\) 则非 \(s\) 的限制，我们需要从 \(t\) 向它的祖先对应的所有字符串的 否定 连边。因此，建出根向字典树和叶向字典树。在两棵字典树上，每个字符串对应的状态向它对应文字的否定连边。为防止出现 \(s\) 和 \(t\) 对应同一字符串的情况，在叶向字典树上，\(s\) 对应文字只能向它对应状态的两个儿子连边，否则 \(s\) 会向 \(s\) 的否定连边，导致必然无解。同理，在根向字典树上，\(s\) 对应文字向它对应结点的父亲（而非它本身）连边。

我们还要处理 \(s = t\) 但对应不同字符串的情况。容易发现，将相等的字符串排成一行，每个字符串会向所有除了它本身的其它字符串的 否定 连边，可以通过前缀后缀优化建图做到。

综上，点数和边数关于 \(n\) 和字典树大小 \(m\) 线性。点数不超过 \(4n + 2m\)，而 \(m \leq 2n\)，所以边数不超过 \(8n\)。代码。

*[ARC161E] Not Dyed by Majority (Cubic Graph)

好题。

考虑操作前的序列，因为全黑和恰有一白对应相同结果，所以一定有解。

将距离一个点为 \(2\) 的所有点染成同一种颜色，那么该点染黑或染白对最终结果没有影响。因此至少有 \(\frac 1 {2 ^ 6}\) 的操作后序列无解。因为有很多点，所以实际比例要大得多。不过 \(\frac {1} {64}\) 已经够用了。

随机，判定是否无解是容易的：2-SAT 即可。代码。

2. 点双进阶：广义圆方树

前置知识：Tarjan 求割点。

关于点双相关基础知识，见 “图论基础”。

广义圆方树是刻画无向图上点必经性的强力工具，是用于解决仙人掌上问题的圆方树的扩展，以下简称 圆方树 (block forest)。它是点双缩点的产物，描述了原图任意两点之间的所有割点，即 \(u, v\) 之间的所有必经点。

点双缩点和边双缩点的方法类似，都是借助 Tarjan 算法求出所有连通分量的形态。但是它们缩点得到的结构不同：每个点恰好属于一个边双（相对应地，每条边恰好属于一个点双），所以边双缩点时可以将边双内部的所有点看成一个点。但一个点可能出现在多个点双中（这样的点一定是割点）。而且，为了刻画必经点，我们希望在缩点时保留所有割点，而不能将它们缩起来，就像边双缩点时保留了所有割边一样。

2.1 算法介绍

考察一个点双。如果我们希望将它缩成一棵树，且树上任意两点之间的简单路径恰为它们之间的所有必经点，那么因为点双内不存在必经点，所以任意两点都必须直接相连，但是这和 “缩成一棵树” 矛盾。

尝试建出点双的 “代表点” 并向点双内所有点连边，发现这样形成的菊花图满足条件：任意两点通过代表点间接地直接相连，不经过点双内其它点。经过代表点则可以理解为必须经过这个点双。

这自然地引出了圆方树的定义：将原图的点视为圆点，对于原图的每个点双，删去其中所有边，新建代表该点双的方点连向点双内所有圆点，形成的结构称为圆方树。每个点双缩成一张菊花图，多个菊花图通过原图割点连接（割点是点双的分隔点），类比边双缩点时，每个边双缩成一个点，多个边双通过原图割边连接。

如下图，黑色虚线表示原图的边，每个颜色表示一个点双连通分量，不同颜色的实边表示对应点双连通分量缩成的菊花图。黑色的 \(4\) 和 \(8\) 就是原图的割点，它们属于多个点双连通分量。

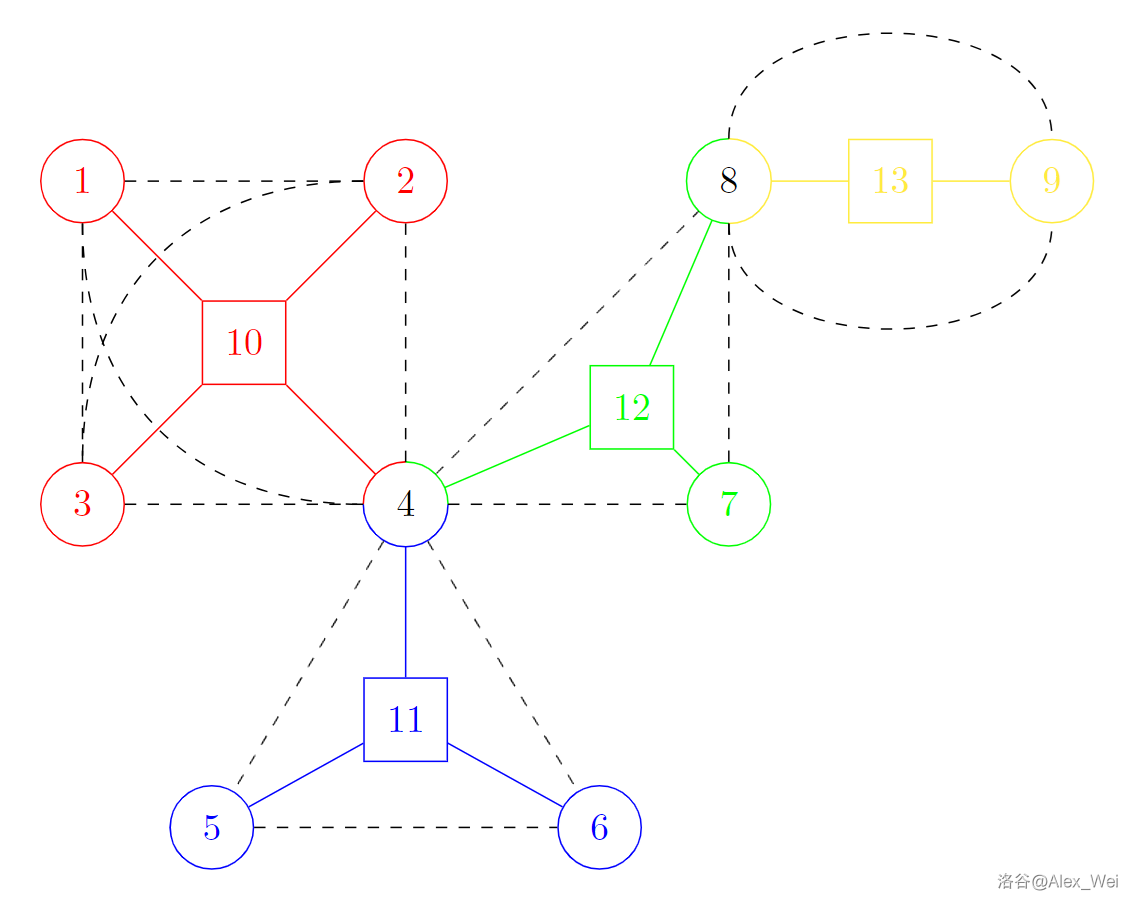
圆方树的建法只需在 Tarjan 求割点的基础上稍作修改。从结点 \(v\) 回溯至其父结点 \(u\) 时，若 \(low_v \geq dfn_u\)，说明 \(v\) 及其子树在栈内的部分与 \(u\) 共同形成一个点双。新建代表该点双的方点，弹出栈顶直到 \(v\) 被弹出，弹栈过程中圆点与方点连边。注意 不能弹出 \(u\)，因为 \(u\) 可能和它别的儿子形成另外的点双，所以需要特殊处理 \(u\)。正确性参考边双和 SCC 缩点的证明。

时间复杂度 \(\mathcal{O}(m)\)。

注意：

• 处理完每个连通块后栈内会剩下一个点，为该连通块 DFS 树的根。
• 每个点双新建一个方点，需要开两倍空间存储圆方树。当图是一张菊花时，点双数量为 \(n - 1\)。

用该算法求点双连通分量时：

• 与边双缩点和割点判定不同的是，我们不需要将栈内剩下的点单独作为一个点双，也不需要特殊处理根结点。因为在根结点上用非根割点判定法则，每个儿子都会将根判定为割点，这正好是我们想要的：根结点和每个儿子子树在栈内的部分均形成一个点双。因此，不存在没有被考虑到的点双，也没有多余的点双。
• 特判孤立点。

圆方树小技巧：

• 判定一条边 \((u, v)\) 属于哪个点双，也就是求出 \(u, v\) 之间（它们距离为 \(2\)）唯一的方点。若 \(u, v\) 的父亲相同，则方点是它们共同的父亲。若 \(u, v\) 的父亲不同，则方点是深度较深的结点的父亲。
• 对于仙人掌的每个环，对应方点的所有邻点的顺序就是环上所有点的顺序。这是因为 Tarjan 是通过 DFS 实现的，所以对应方点的加入邻点的顺序一定是从当前点开始绕环一周。

点双缩点 代码。圆方树代码见例题 P5058。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 5e5 + 5;
int n, m;
vector<int> e[N];
vector<vector<int>> ans;
int dn, dfn[N], low[N], stc[N], top;
void form(int id, int it) {
  vector<int> S = {id};
  for(int x = 0; x != it; ) S.push_back(x = stc[top--]);
  ans.push_back(S);
}
void tarjan(int id) {
  dfn[id] = low[id] = ++dn;
  stc[++top] = id;
  for(int it : e[id]) {
    if(!dfn[it]) {
      tarjan(it), low[id] = min(low[id], low[it]);
      if(low[it] >= dfn[id]) form(id, it); // 写 low[it] == dfn[id] 也可以, 因为 low[it] <= dfn[id]
    }
    else low[id] = min(low[id], dfn[it]);
  }
}
int main() {
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++) {
    int u, v;
    cin >> u >> v;
    if(u == v) continue;
    e[u].push_back(v);
    e[v].push_back(u);
  }
  for(int i = 1; i <= n; i++) {
    if(e[i].empty()) ans.push_back({i});
    else if(!dfn[i]) tarjan(i);
  }
  cout << ans.size() << "\n";
  for(auto S : ans) {
    cout << S.size() << " ";
    for(int it : S) cout << it << " ";
    cout << "\n";
  }
  return 0;
}

2.2 圆方树的性质

回忆必经点的定义：从 \(x\) 到 \(y\) 必须经过的点，即 \(x\) 到 \(y\) 的所有路径的交集。

回忆点双的性质：

• 点双交点的唯一性：若两点双有交点，则交点唯一。
• 边的点双连通性：直接相连的两点点双连通。

在图论基础部分，我们给出了点双最重要的基本性质：

对于 \(n\geq 3\) 的点双内的任意两点 \(x, y\)，存在经过 \(x, y\) 的长度不小于 \(3\) 的简单环。

等价表述：对于 \(n\geq 3\) 的点双内的任意两点 \(x, y\)，存在两条端点为 \(x, y\) 且仅在端点处相交的路径。

在研究圆方树前，给出以下引理：

引理 1

\(z\) 不是 \(x, y\) 的必经点当且仅当存在不经过 \(z\) 的连接 \(x, y\) 的路径。

证明

根据必经点的定义，显然。\(\square\)

引理 2

\(z\) 是 \(x, y\) 的必经点当且仅当删去 \(z\) 后 \(x, y\) 不连通。

证明

删去 \(z\) 后 \(x, y\) 连通等价于存在不经过 \(z\) 的连接 \(x, y\) 的路径，根据引理 1，等价于 \(z\) 不是 \(x, y\) 的必经点。因此，删去 \(z\) 后 \(x, y\) 不连通等价于 \(z\) 是 \(x, y\) 的必经点。\(\square\)

结合割点与点双连通的定义，易知：

推论

\(x, y\) 点双连通当且仅当不存在必经点 \(z\neq x, y\)。

引理 3

若 \(z\) 与 \(x, y\) 均点双连通，但 \(x, y\) 不点双连通，则 \(z\) 是 \(x, y\) 的必经点。

证明

考虑包含 \(x, z\) 的点双 \(S_1\) 和包含 \(y, z\) 的点双 \(S_2\)。根据点双交点唯一性，\(S_1\cup S_2 = \{z\}\)。根据点双基本性质，考虑 \(x\to z\) 的两条仅在端点处相交的路径 \(P_1, P_2\subseteq S_1\) 和 \(z\to y\) 的两条仅在端点处相交的路径 \(P_3, P_4\subseteq S_2\)。\(P_1\to P_3\) 和 \(P_2\to P_4\) 两条路径使得 \(x, y\) 之间只有 \(z\) 可能是必经点，再结合 \(x, y\) 不点双连通与引理 2 的推论得证。\(\square\)

引理 4

\(x\) 是割点当且仅当 \(x\) 属于至少两个点双。

证明

若 \(x\) 是割点，则删去 \(x\) 后存在与 \(x\) 相邻的 \(y, z\in N(x)\) 满足 \(y, z\) 不连通，否则易证整张图仍连通。因此 \(x\) 是 \(y, z\) 的必经点，\(y, z\) 不点双连通。根据边的点双连通性，\(x, y\) 点双连通，\(x, z\) 点双连通，因此 \(x\) 属于至少两个点双。

若 \(x\) 属于至少两个点双，则根据边的点双连通性，存在 \(y, z\) 使得 \(x, y\) 点双连通，\(x, z\) 点双连通，但 \(y, z\) 不点双连通。根据引理 3，\(x\) 是 \(y, z\) 的必经点，因此 \(x\) 是割点。\(\square\)

结合上述引理，回忆图的点双结构的形态：点双交点为割点，若干点双由公共割点相连，形成树状结构。在此基础上，得到圆方树的基本结构：

• 圆点 \(x\) 的度数等于包含它的点双个数。
• 方点 \(x\) 的度数等于它对应的点双大小。
• 圆点 \(x\) 不是叶子当且仅当它是原图的割点（引理 4）。
• 圆方树上圆方点相间。
• 连通无向图的圆方树连通（相邻两点点双连通）。
• 原图的每个连通分量对应一棵连通的圆方树。

我们提出圆方树的目的是刻画无向图上点的必经性，可以证明它确实做到了这一点。

性质 1

原图删去 \(x\) 后剩余结点的连通性等于在圆方树上删去 \(x\) 后剩余结点的连通性。

证明

对任意不同于 \(x\) 的两点 \(y\neq z\) 以及它们之间的任意一条简单路径 \(P\)，若 \(P\) 经过 \(x\)，则必然在经过 \(x\) 之前经过 \(x\) 的某个邻居，且在经过 \(x\) 之后经过 \(x\) 的另一个邻居。因此，只需证明 \(x\) 的所有邻居之间的连通性相等。这是证明删点后连通性不变的常用手段。

考虑 \(x\) 的任意两个邻居 \(y\neq z\)，则 \(x, y\) 点双连通，\(x, z\) 点双连通。

• 若原图删去 \(x\) 后 \(y, z\) 连通，则 \(y, z\) 点双连通，\(x, y, z\) 属于同一点双，存在方点 \(e\) 同时连接圆点 \(x, y, z\)，圆方树删去 \(x\) 后 \(y, z\) 通过 \(e\) 连通。
• 若原图删去 \(x\) 后 \(y, z\) 不连通，则存在方点 \(e_1\) 连接圆点 \(x, y\)，方点 \(e_2\) 连接圆点 \(x, z\)。因此 \(x\) 落在 \(y, z\) 在圆方树上的简单路径，圆方树删去 \(x\) 后 \(y, z\) 不连通。\(\square\)

性质 2

圆点 \(x, y\) 在圆方树上的简单路径上的所有圆点恰为原图 \(x, y\) 之间的必经点。

证明

若圆点 \(z\neq x, y\) 在圆点 \(x, y\) 的简单路径上，则根据性质 1，原图删去 \(z\) 后 \(x, y\) 不连通，\(z\) 为 \(x, y\) 的必经点。若 \(z\) 为 \(x, y\) 的必经点，则原图删去 \(z\) 后 \(x, y\) 不连通，根据性质 1，圆点 \(z\) 在圆点 \(x, y\) 的简单路径上。\(\square\)

推论

在性质 2 的基础上，原图 \(x\) 到 \(y\) 的任意简单路径上所有必经点出现的顺序恰为圆方树 \(x\) 到 \(y\) 的唯一的简单路径上所有圆点依次出现的顺序。

这些性质全部在描述一个核心结论：若 \(z\) 在圆方树上是 \(x, y\) 的必经点，则在原图上也是。换言之，圆方树精确地刻画了原图的必经性。

圆方树最主要的应用是：当题目只关心无向图必经性时，可以将图上问题转化为树上问题。用圆方树判定必经性（两点之间的边必经性和点必经性均可使用圆方树判定）的方法见例题 P4334。

2.3 例题

P5058 [ZJOI2004] 嗅探器

建出圆方树，那么 \(a, b\) 两点之间的所有圆点（割点）的编号最小值即为所求。注意不能包含 \(a, b\) 本身。

如果不存在这样的圆点则无解，此时 \(a, b\) 点双连通。

时间复杂度 \(\mathcal{O}(n + m)\)。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 4e5 + 5;
int n, a, b, node;
int dn, dfn[N], low[N], top, stc[N];
vector<int> e[N], g[N];
void tarjan(int id) {
  dfn[id] = low[id] = ++dn, stc[++top] = id;
  for(int it : e[id]) {
    if(!dfn[it]) {
      tarjan(it), low[id] = min(low[id], low[it]);
      if(low[it] == dfn[id]) {
        g[++node].push_back(id);
        g[id].push_back(node);
        for(int x = 0; x != it; ) {
          g[node].push_back(x = stc[top--]);
          g[x].push_back(node);
        }
      }
    }
    else low[id] = min(low[id], dfn[it]);
  }
}
int fa[N], dep[N];
void dfs(int id, int ff) {
  fa[id] = ff, dep[id] = dep[ff] + 1;
  for(int it : g[id]) if(it != ff) dfs(it, id);
}
int main() {
  cin >> n, node = n;
  scanf("%d%d", &a, &b);
  while(a && b) {
    e[a].push_back(b), e[b].push_back(a);
    scanf("%d%d", &a, &b);
  }
  tarjan(1), dfs(1, 0);
  scanf("%d%d", &a, &b);
  int ans = N;
  if(dep[a] < dep[b]) swap(a, b);
  while(dep[a] > dep[b]) if((a = fa[a]) != b) ans = min(ans, a);
  while(a != b) ans = min(ans, min(a = fa[a], b = fa[b]));
  if(ans > n) puts("No solution");
  else cout << ans << "\n";
  return 0;
}

P4334 [COI2007] Policija

对于类型 \(1\) 的询问，相当于检查 \(e = (G_1, G_2)\) 是否为 \(A, B\) 的必经边。

对于类型 \(2\) 的询问，相当于检查 \(C\) 是否为 \(A, B\) 的必经点。

建出圆方树。

对于类型 \(1\) 的询问，设 \(c\) 表示 \(e\) 所在点双对应的方点。首先判断 \(e\) 是否为割边，等价于判断 \(c\) 的度数是否为 \(2\)。若否，则 \(e\) 不是割边，因原图连通，删去后 \(A, B\) 仍连通。若是，则检查 \(G_1, G_2\) 是否均为 \(A, B\) 之间的必经点，等价于检查 \(c\) 是否落在 \(A, B\) 在圆方树上的简单路径上。

对于类型 \(2\) 的询问，直接判定 \(C\) 是否落在 \(A, B\) 在圆方树上的简单路径上即可。

判定某点是否落在两点简单路径上是容易的：若 \(c\) 落在 \(a, b\) 的简单路径上，则 \(c\) 必须落在 \(lca(a, b)\) 的子树内，且 \(a\) 或 \(b\) 必须落在 \(c\) 的子树内。

时间复杂度 \(\mathcal{O}(((n + q)\log n + m)\)，瓶颈在于求 LCA。代码。

P4630 [APIO2018] Duathlon 铁人两项

首先进行转化，对所有点对 \((u, v)\)，求它们之间简单路径的并去掉 \(u, v\) 之后的点集大小之和。

由于本题简单路径定义为不经过重复点的路径，且题目考察连通性相关，不难想到建出圆方树。因此相当于求 \((u, v)\) 之间所有方点所表示的点双大小之和。

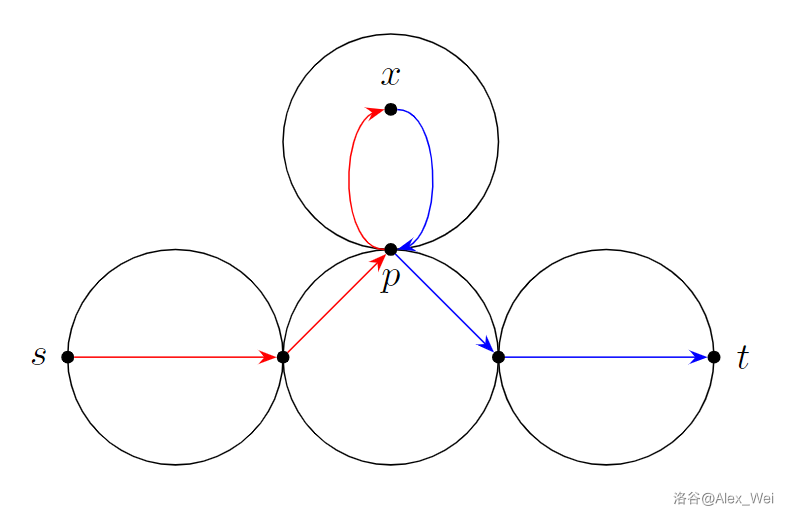
注意，路径上每个除了 \(u, v\) 以外的割点会被算到两次，而 \(u, v\) 本身也会被路径上它们所在的点双算入一次。这说明路径上每个圆点都被多算了一次。因此，每个方点的贡献是其对应的点双大小，而每个圆点的贡献是 \(-1\)。

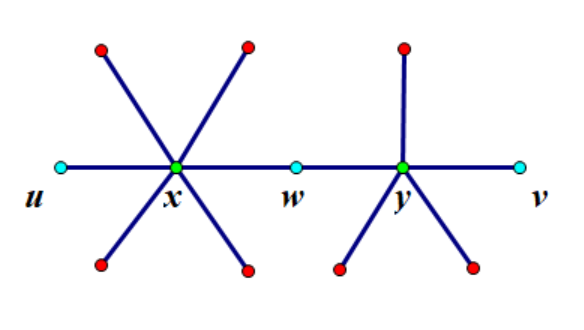
如上图，从最左边的 \(u\) 到最右边的 \(v\)，路径上共有两个方点 \(x, y\)。单纯将它们的权值加起来会得到 \(6 + 5 = 11\)。但我们发现正确的答案应该是 \(8\)，因为只有所有红点和 \(w\) 才会作为中转点。错误原因是 \(u, v, w\) 均被多算了一次，真正的答案由 \(-1 + 6 -1 + 5 - 1\) 求得。

设每个点的权值为 \(a\)，问题等价于求 \(\sum\limits_{u \neq v \land u, v\leq n} \sum\limits_{p \in \mathrm{path}(u, v)} a_p\)。一般而言，我们用大于 \(n\) 的数值给方点标号（见上一题代码），所以有限制 \(u, v\leq n\)。

转换贡献方式，考察圆方树上每个结点对答案的贡献。容易通过一遍 DFS 求出子树大小的同时求解该问题。

注意原图可能不连通。

时间复杂度线性。代码。

CF1763F Edge Queries

建出圆方树，则 \(a, b\) 之间涉及到的所有点双即 \(a, b\) 在圆方树简单路径上的所有方点。

对于 \(a, b\) 路径上的一个点双，如果其不为两点一边即割边，则删去其中任意一条边 \(a, b\) 仍相互可达。因此，对于所有点双，若其为两点一边，则给其对应方点赋值 \(0\)，否则赋点双内部边数作为权值，询问 \(a, b\) 的答案即 \(a, b\) 在圆方树上的简单路径上的所有方点的权值之和。

视 \(n, m, q\) 同级，时间复杂度 \(\mathcal{O}(n\log n)\)。代码。

P4606 [SDOI2018] 战略游戏

删去某结点后 \(u\) 不能到达 \(v\)，说明该结点是 \(u, v\) 之间的必经点。因此，建出圆方树，题目相当于求点集 \(S\) 在树上的虚树所包含的不属于 \(S\) 的圆点数量。

对每个点是否为圆点做树上前缀和，以计算虚树上一条边的贡献（不含两端）。再加上所有不属于 \(S\) 但是为虚树结点的圆点的贡献。

时间复杂度线性对数。代码。

*P3225 [HNOI2012] 矿场搭建

不那么套路的连通性相关题目。

题目希望我们给出一种选择关键点的方式，满足删去任何一个点后形成的每个连通块内都存在至少一个关键点。

首先，关键点数量至少为 \(2\)，因为若关键点数量为 \(1\)，则若删去关键点就寄了。

进一步地，由于删去非割点后整张图仍连通，所以删去非割点后连通块存在关键点蕴含于删去割点后连通块存在关键点。唯一的特例是不存在割点，整张图点双连通。此时关键点数量最小值显然为 \(2\)，且从图上任选两点作为关键点均合法，方案数为 \(\binom{|V|} {2}\)。

特判后，每个点双至少有一个原图上的割点。

为了解题，我们需要深入剖析圆方树的结构。剔除圆方树上所有叶子，即原图的非割点，我们得到了圆方树的由原图割点和点双方点构成的骨架，称为块割树。

定义一个点双的度数等于它对应的方点在块割树上的度数，等价于该点双包含的原图割点数量。

考虑一个大小为 \(s\) 的点双。若其度数为 \(1\)，那么它是块割树的叶子，其内部需要有一个关键点（否则删去它包含的唯一割点，其内部不存在关键点），方案数为 \(s - 1\)。否则它有大于一个割点，若其包含的任意一个割点被删去，总可以走其它割点到达某个块割树的叶子，因此其内部不需要割点。

删去主干树上任何一个割点，形成的每个连通块至少包含一个主干树的叶子，因此方案合法。

综上，令主干树的叶子对应点双大小分别为 \(s_1, s_2, \cdots, s_k\)，则第一问的答案为 \(k\)，第二问的答案为 \(\prod_{i = 1} ^ k(s_i - 1)\)。

时间复杂度 \(\mathcal{O}(n + m)\)。代码。

CF487E Tourists

一道圆方树经典题。

\(c\) 在 \(a\to b\) 的简单路径上当且仅当 \(c\) 与 \(a\to b\) 某个方点相邻。因此，令方点的权值为对应点双所有结点权值最小值，将圆方树树剖即可回答询问。

问题在于修改点权时可能影响到很多方点权值，无法承受。考虑使用 只维护儿子信息 的技巧，将方点权值改为所有儿子的权值最小值，用 multiset 维护。修改圆点权值时修改其父结点的 multiset 并更新其父结点权值。

查询同样求出 \(a\to b\) 点权最小值。当 LCA 为方点时，答案还要与其父结点（若存在）取最小值。

时间复杂度 \(\mathcal{O}((n + q\log n)\log n)\)。代码。

*P8456 「SWTR-8」地地铁铁

题解。

*P8331 [ZJOI2022] 简单题

因为简单路径不包含重复点，所以建出圆方树。考虑 \(S\rightsquigarrow T\) 的所有必经点 \(p_1, p_2, \cdots, p_k\)，其中 \(p_1 = S\)，\(p_k = T\)。如果能算出 \(p_i\rightsquigarrow p_{i + 1}\) 的简单路径数和权值和，就可以合并这些结果求出答案。

对每个深度大于 \(2\) 的圆点，预处理它到它父亲（对应点双）的父亲（另一个圆点）的信息。如果 \(S, T\) 的 LCA 是圆点，根据预处理的信息树上倍增。如果是方点，那么倍增到方点的两个儿子 \(S', T'\)，再计算 \(S' \rightsquigarrow T'\) 的信息。

也就是说，我们需要支持：给定点双连通分量，\(\mathcal{O}(m)\) 预处理，\(\mathcal{O}(1)\) 计算点双任意两个点之间的简单路径数和权值和。对于一般点双这是 NP 问题，所以题目给出的性质很关键。

通过推导后，可以证明若原所有简单环长相等，那么点双只能是 “杏仁”：存在 \(S, T\) 和边的划分使得每个划分恰好是 \(S, T\) 之间的一条路径，且所有路径在除了 \(S, T\) 以外的地方 点不相交。这样一来，求任意两点简单路径数和权值和是容易的，分类讨论即可。

时间复杂度 \(\mathcal{O}((n + m + q)\log n)\)。代码。

3. 连通性进阶：耳分解与双极定向

前置知识：无向图 DFS 树，有向图 DFS 树，双连通分量、圆方树。

一个小众而简单的知识点，有助于加深对 DFS 树的理解。

3.1 相关定义

• 耳：在无向图 \(G\) 上，简单路径或简单环 \(P: v_0 \to \cdots \to v_k\) 称为子图 \(G' = (V', E')\subseteq G\) 的 耳，若 \(v_0, v_k\in V'\) 且 \(v_{1\sim k - 1}\notin V'\)。
• 开耳：在耳的基础上，若 \(P\) 是简单路径（\(v_0\neq v_k\)），则 \(P\) 称为 \(G'\) 的 开耳。
• 耳分解：将无向连通图 \(G\) 划分为若干耳的方案称为 耳分解 (ear decomposition)。具体地，耳分解是一系列无向连通图 \(G_0, \cdots, G_k\)，满足 \(G_i\) 是 \(G_{i - 1}\) 添加一个耳，且 \(G_0\) 是一个点或一个简单环。当所有 \(G_i\) 是 \(G_{i - 1}\) 添加一个开耳时，称为 开耳分解。

注意 \(G_0\) 可以是简单环，因为一个点不存在开耳。否则开耳分解的定义就是无效的。

类似定义有向图上的耳、开耳和耳分解。

• 双极定向：无向连通图 \(G\) 关于 \(s, t(s\neq t)\) 的 双极定向 (bipolar orientation) 是给所有无向边的一种定向方案，满足定向后的图是 DAG，且 \(s\) 是唯一没有入度的点，\(t\) 是唯一没有出度的点。因为 \(s, t\) 是定向的两极，所以称为双极定向。

3.2 耳分解

先考虑什么样的 无向图 存在耳分解。如果一张图存在耳分解，那么每条边恰好属于一个耳。耳是简单路径或简单环，这启发我们考虑双连通图。

不存在含割边的简单环，且含割边的简单路径的两端一定在割边两侧。因为耳分解初始的所有点在割边的同一侧，而如果想包含割边另一侧的点，就必须从割边一侧走过去再走回来，显然不可能，所以 非边双没有耳分解。

3.2.1 边双连通图

在边双连通图上，对每条边，存在经过这条边的简单环。容易想到每次选择一条连接 \(V'\) 和 \(G\backslash V'\) 的边 \((u, v)\)，求出经过这条边的简单环，在环上从 \(u\to v\) 出发直到再次回到 \(V'\)，那么经过的路径就是一个耳。于是 边双有耳分解。

这样构造比较麻烦，我们需要更简单的方法。图论相关的构造题，首先考虑 DFS 树。

方法一

考虑以 \(1\) 为根的 DFS 树，初始 \(G_0 = (\{1\}, \varnothing)\)。因为无向图 DFS 树的非树边两端具有祖先后代关系，考虑每一条以 \(1\) 为祖先的非树边 \((1, x)\)，从 \(x\) 开始不断跳父亲直到落在当前的 \(G'\)，那么 \(1\to x \to fa_x \to \cdots\) 是一个耳。然后加入所有以 \(1\) 的儿子为祖先的非树边，以此类推。因为每条树边被至少一条非树边覆盖，所以到每个点时，这个点一定在当前的 \(G'\) 上，即构造合法。

如下图，返祖边由弧线表示。首先根据返祖边 \(3\to 1\) 得到红色的耳，然后根据返祖边 \(5\to 1\) 得到蓝色的耳，最后根据返祖边 \(4\to 3\) 得到绿色的耳。注意边的方向和实际的 DFS 树相反，这是为了表现 \(u\to x \to fa_x \to \cdots\) 求一个耳的过程。

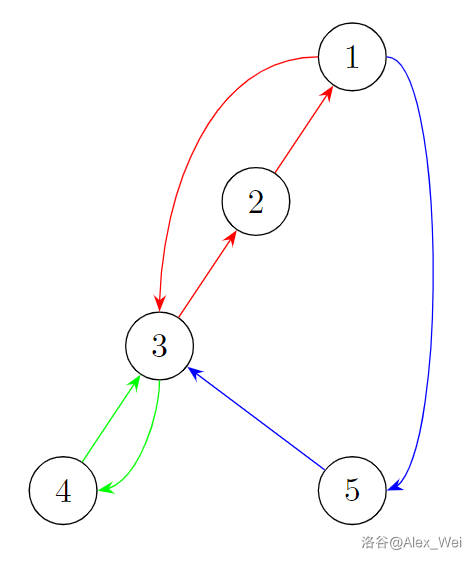
方法二

考虑边双的性质：\(low_y \leq dfn_x\)。考虑按时间戳从小到大依次加入每个点（即 按原 DFS 顺序再 DFS 一遍）。在加入时间戳为 \(i(i\geq 2)\) 的点 \(y\) 时，\(G'\) 含所有时间戳小于 \(i\) 的点。

考虑 \(y\) 的父亲 \(x\)。因为图是边双，根据割边的判定条件，\(low_y \leq dfn_x\)，所以存在 \(y\) 的后代 \(u\) 满足 \(u\) 可以从返祖边向上回到某个时间戳小于 \(i\) 的点 \(d\)（\(x\) 或其祖先）。于是，从 \(x\) 出发走树边到 \(u\)，再从 \(u\) 一步返回 \(G'\)，得到 \(G'\) 的含 \(y\) 的耳。

如下图，红色是 \(G'\) 的点，蓝色是新加入的耳。

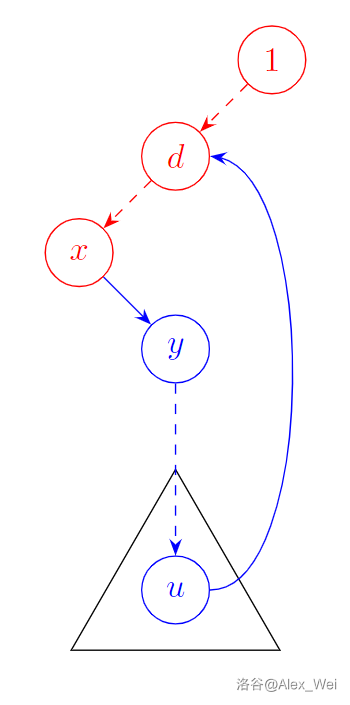
最后 \(G'\) 包含所有点，将剩下的边依次加入即可。

两个方法的时间复杂度均为 \(\mathcal{O}(m)\)。

3.2.2 点双连通图

设 \(n\geq 3\)，此时点双是边双，所以点双也有耳分解。

考虑点双的性质：对 \(n\geq 3\) 且 无自环 的点双内任意不同两点 \(s, t\) 和一边 \(e\)，存在以 \(s, t\) 为两端且经过 \(e\) 的路径。容易想到从初始任意简单环开始，每次选择 \(s, t\in V'(s\neq t)\) 和 \(e\notin E'\)，找到以 \(s, t\) 为两端且经过 \(e\) 的路径 \(P\)。从 \(e\) 往前往后分别找到第一个在 \(V'\) 的点 \(s'\) 和 \(t'\)，就是一个包含 \(e\) 的开耳。这说明 \(n\geq 3\) 的无自环点双有开耳分解。

相反，如果图上有割点，那么容易证明没有开耳分解。

此时，使用边双连通的耳分解构造方法，就能得到开耳分解：

方法一

到点 \(x\) 时，考虑 \(x\) 的任意儿子 \(y\)。因为 \(x\) 不是割点，所以 \(y\) 的子树存在返祖边可达 \(x\) 的祖先（不含 \(x\)），于是此时 \((x, y)\in E'\)，即 \(y\in V'\)。因此，新增的以 \(x\) 为一端的耳无论如何都会停在 \(y\) 的子树内，所以是开耳。

特别地，对于根结点 \(1\)，选任意以 \(1\) 为一端的返祖边得到初始简单环，此时 \(1\) 的所有儿子落在 \(V'\)，这是因为 \(1\) 不是割点，只有一个儿子。

方法二

利用 \(low_y < dfn_x\) 类似证明。特别地，对于唯一的父结点为根（时间戳为 \(2\)）的结点，其属于初始简单环。

两个方法的时间复杂度均为 \(\mathcal{O}(m)\)。

3.2.3 强连通图

对于有向强连通图 \(G\)，若 \(V'\neq V\)，则存在有向边 \(u\to v\) 满足 \(u\in V'\) 且 \(v\notin V'\)。因为 \(G\) 强连通，所以存在 \(v\) 返回 \(u\) 的路径。取路径第一次走到 \(V'\) 之前的段，接在 \(u\to v\) 后，就是 \(G'\) 的耳。于是 强连通图有耳分解。

在不断加入耳的过程中，\(G'\) 时刻保持强连通。所以 非强连通图没有耳分解。

构造方案和边双方法二一样：对所有非根结点 \(y\)，\(low_y < dfn_y\)。时间复杂度 \(\mathcal{O}(m)\)。

3.3 双极定向

关于双极定向的另一种等价定义，见 3.3.3 小节。

3.3.1 点双连通图

边双不一定有双极定向：\(E = \{(1, 2), (1, 2), (1, 3), (1, 3)\}\)，\(s = 1\)，\(t = 3\)。在尝试使用耳分解构造双极定向的过程中，我们发现 DAG 要求无环，但耳可以是简单环，导致无法双极定向。这启发我们考虑具有开耳分解的图，也就是 \(n\geq 3\) 的无自环点双。

通过开耳分解构造双极定向：以 \(s\) 为根 DFS。以 \(s\) 到 \(t\) 的树上路径作为 \(G_0\)，将路径上的所有边定向为 \(s\) 到 \(t\) 的方向。不断加入 \(G'\) 的开耳，根据开耳两端的拓扑序大小决定开耳上边的方向。容易归纳证明任何时刻 \(E'\) 的定向方案都是 \(G'\) 的双极定向，满足 \(s\) 是唯一没有入度的点，\(t\) 是唯一没有出度的点。

但是如果直接做则需要维护拓扑序，支持插入以及查询两个数在拓扑序上的前后关系，不能做到线性时间。我们必须快速确定耳的方向。

考虑方法二，则 \(x\) 是耳的一端。设 \(a\) 是耳的另一端，则 \(a\) 是 \(x\) 的祖先。设 \(a\) 在 \(x\) 方向上的儿子为 \(b\)。

结论

设树边 \((x, y)\)，其中 \(x\) 是 \(y\) 的父亲。若定向为 \(x\to y\)，则 \(y\) 子树任何点在构造方案的任意时刻不可达 \(x\)。若定向为 \(y\to x\)，则 \(x\) 在构造方案的任意时刻不可达 \(y\) 子树任何点。

若 \(a\to b\)，则 \(x\) 不可达 \(a\)，耳的方向是 \(a\to x\)。若 \(b\to a\)，则 \(a\) 不可达 \(x\)，耳的方向是 \(x\to a\)。根据新增耳的定向和原来的 \(G'\) 满足上述结论，可以证明新的 \(G'\) 仍满足上述结论。初始结论成立，由数学归纳法知算法正确。

如下图，红色边 \(a\to b\) 的方向决定了新加入的耳（蓝色）的方向。

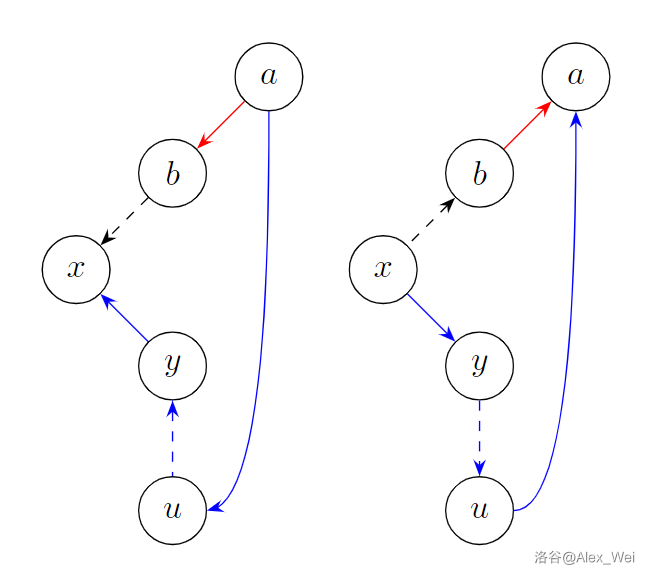
在 DFS 加入每个点的过程中维护根到当前点的路径上每条边的方向，即可 \(\mathcal{O}(1)\) 求出 \((a, b)\) 的定向。时间复杂度 \(\mathcal{O}(m)\)。代码见例题 P9394。

3.3.2 一般无向图

然而，并非只有点双才有双极定向：\(E = \{(1, 2), (2, 3)\}\)，\(s = 1\)，\(t = 3\)。

建出一般无向图 \(G\) 的圆方树，考虑树上 \(s\) 到 \(t\) 的路径 \(p_0 \to C_1\to p_1\to \cdots \to C_k\to p_k\)，其中 \(C_i\) 是方点。求出 \(C_i\) 的从 \(p_{i - 1}\) 到 \(p_i\) 的双极定向，得到这些点双的并所形成子图（是一个毛毛虫）的 \(s\) 到 \(t\) 的双极定向。

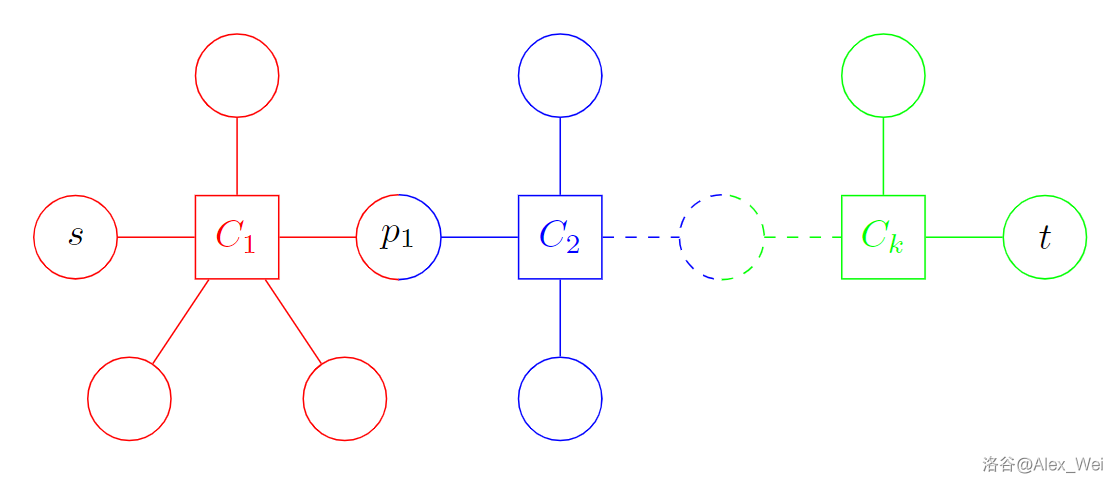
如果有结点 \(x\) 不在子图上，根据圆方树的结构，存在割点 \(p\) 使得删去 \(p\) 后 \(s\rightsquigarrow t\) 和 \(x\) 不连通。

假设 \(G\) 存在双极定向，因为 \(t\) 是唯一没有出度的点，所以存在 \(x\) 到 \(t\) 的路径。而 \(p\) 是 \(x\) 和 \(t\) 之间的必经点，所以存在 \(x\) 到 \(p\) 的路径。同理，由 \(s\) 是唯一没有入度的点以及 \(p\) 是 \(x\) 和 \(s\) 之间的必经点可知存在 \(p\) 到 \(x\) 的路径，得到环，和双极定向的结果无环矛盾。因此，当且仅当 \(s\) 到 \(t\) 的路径上经过了所有方点时，\(G\) 存在双极定向，且方案由每个点双的定向方案合并得到。

这等价于 \(s\) 和 \(t\) 在圆方树上的路径经过所有方点，等价于加入 \((s, t)\) 之后 \(G\) 点双连通，等价于圆方树是毛毛虫。求一般图的双极定向和求点双的双极定向的实现方法几乎一致。

3.3.3 更简单的写法

来自 rainbow_sjy，链接见参考资料部分。考虑点双连通图 \(G\)。

能够定向成 DAG 就有拓扑序，而拓扑序意味着什么呢？注意到不可能有未访问的结点指向访问的结点，所以任意时刻已经访问的结点形成含 \(s\) 的连通块，未访问的结点形成含 \(t\) 的连通块。如果能够给出图上所有结点的一个排序，使得任意前缀与任意后缀都是连通块，那么将所有边定向为由较小的位置指向较大的位置就是合法的双极定向。注意所有前后缀是连通块的必要性：这保证了 \(s\) 是唯一入度为 \(0\) 的点，\(t\) 是唯一出度为 \(0\) 的点。

不要给边定向，而是直接求出这个排序。从 \(s\) 开始依次将每个点从图上删去，最后删 \(t\)，由删点的顺序确定排序。

引理

如果一个点 \(x\) 的度数为 \(1\)，那么它可以立刻删去。

证明

删去的点形成连通块：因为 \(G\) 点双连通，所以每个点的初始度数不小于 \(2\)。如果 \(x\) 的度数 \(1\)，那么在此之前存在和它相邻的点被删去。

没有删去的点形成连通块：因为 \(G\) 点双连通，所以删去 \(s\) 时剩下的图连通。而删去度数为 \(1\) 的叶子不会影响图的连通性。

由 Tarjan 算法，对每个点只保留最浅的返祖边不影响图的点双连通性。处理过后，DFS 树的叶子的度为 \(2\)，分别和 \(low_x\) 和 \(fa_x\) 连边。根据引理，我们可以进行缩二度点操作：如果 \(low_x\) 或 \(fa_x\) 被删去，那么可以立刻删去 \(x\)。于是我们直接从图上删去 \(x\)，加入 \((fa_x, low_x)\)。显然，新的图还是点双连通的，所以依然可以进行以上操作。需要注意不能把 \(t\) 缩掉。当 \(t\) 是唯一的叶子时，DFS 树的形态是 \(s\) 到 \(t\) 的一条链，此时剩下的处理是平凡的。

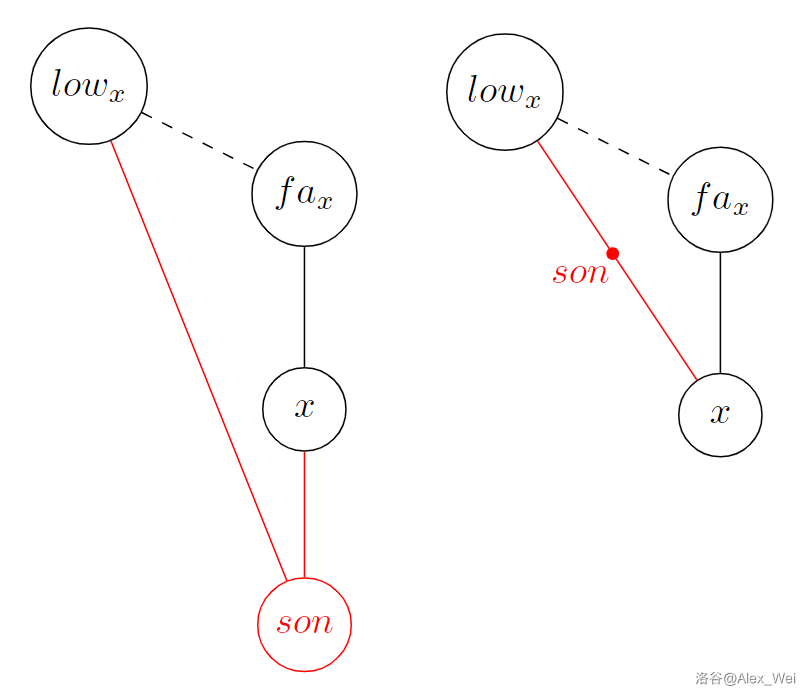
具体怎么实现呢？注意到 \(s\) 到 \(t\) 这条链上的所有点都不会被缩掉，其它点都会被缩掉。非常重要的一点是，在加入 “如果 \(low_x\) 或 \(fa_x\) 被删去，则删去 \(x\)” 的规则时，如果 \(low_x\) 和 \(x\) 的连边本来就是由某个点缩起来的，那么必须先处理 \((low_x, x)\) 这条边对应的规则，例如对 \(x\) 的某儿子 \(son\) 有 “如果 \(low_x\) 或 \(x\) 被删去，则删去 \(son\)”。注意其中的逻辑：必须先执行把点缩起来时加入的规则之后，才能执行缩点图上的规则。

考虑到 DFS 序的倒序一定是缩点序，以及一个点被缩掉的时候一定是加入 \(low_x - x - fa_x\) 的限制（它的儿子可能会产生一些 \((d, x)\) 的缩点边，其中 \(d\) 在 \(low_x\) 到 \(x\) 的路径上，但因为我们只保留最浅的返祖边，所以 \((d, x)\) 会被忽略掉），所以有如下算法：

• 按 DFS 序倒序枚举所有点，如果 \(x\) 不在 \(s\) 到 \(t\) 的树上路径上，那么将 \(x\) 加入 \(low_x\) 和 \(fa_x\) 的列表。
• 按顺序依次访问 \(s\) 到 \(t\) 的树上路径的所有结点。访问一个点时，按列表顺序递归访问其列表，跳过已经访问的结点。
• 访问顺序即合法拓扑序。

这个做法好写很多。代码见 rainbow_sjy 的博客 的方法 1。

3.4 例题

CF555E Case of Computer Network

由耳分解可知边双可被定向为 SCC。

因此，先对原图边双缩点得到一棵树，若 \(s, t\) 不连通则无解，否则，\(s\) 所在边双 \(G(s)\) 必须可达 \(t\) 所在边双 \(G(t)\)，因此 \(G(s)\) 到 \(G(t)\) 的简单路径上所有边的定向确定。如果存在一条边的定向矛盾，则无解，通过 LCA + 树上差分实现对一条链的标记。开两个差分数组分别记录当前点到它父亲的连边是否被钦定为向上或向下，若同时有值则无解。

时间复杂度为 \(\mathcal{O}(m + (n + q)\log n)\)，瓶颈在求 LCA。代码。

P9394 白鹭兰

考虑 \(k = 1\) 的情况。如果满足题目限制，那么点的顺序给出了一个双极定向的方案。相反，如果存在双极定向，那么 DAG 的拓扑序就是点的顺序。由此可知，问题要求最小的 \(k\) 满足缩点图有双极定向。

对 \(G\) 建出圆方树。为了有双极定向，需要缩点让圆方树的形态是毛毛虫。于是我们找到树上的一条链，满足链上最大结点的权值最小，其中

• 方点的权值是所有相邻的不在链上的圆点的子树大小的最大值；
• 圆点的权值是所有相邻的不在链上的方点的子树大小和。

方点和圆点都是向大小最大（圆点数量最多）的子树延伸，且链的 LCA 一定向大小最大和次大的子树延伸。

双极定向构造方案，时间复杂度 \(\mathcal{O}(n + m)\)。代码。

4. 有向图必经点：支配树

前置知识：有向图 DFS 树。

无向图的必经点由割点和割边刻画，有向图同样存在必经点相关的概念与算法：支配点和支配树。学习一般图支配树能够有效提升图论水平！

4.1 定义与性质

首先明确：接下来的所有探究基于 起点固定 这一前提条件。

对一般有向图 \(G = (V, E)\)，选定起点 \(s\)。若 \(s\) 到 \(y\) 的所有路径均经过 \(x\)，则称 \(x\) 支配 (dominate) \(y\)，\(x\) 是 \(y\) 的 支配点。即 \(x\) 是从 \(s\) 到 \(y\) 的必经点。

对 \(s\) 不可达的点讨论支配关系没有意义。不失一般性地，设 \(s = 1\) 且 \(1\) 可达图上所有点。若有多个起点，建立虚点向这些点连边，转化为起点唯一的情况。

和无向图一样，在讨论支配关系时，只考虑 简单路径。如果重复经过一个点，那么将这两次经过之间的点删去。被删去且没有在新路径上出现的点不是支配点。

支配是一种二元关系，我们记作 \(D\)，\(x\) 支配 \(y\) 可以写成 \(xDy\)。从一般二元关系的常见性质出发，探究支配关系所具有的性质：

• 传递性：若 \(xDy\)，\(yDz\)，则 \(1\rightsquigarrow z\) 的任意路径都经过 \(y\)，且 \(1\rightsquigarrow y\) 的任意路径都经过 \(x\)。因此，\(x\) 在 \(1\rightsquigarrow z\) 的任意路径上，即 \(xDz\)。
• 自反性：\(1\rightsquigarrow x\) 的任意路径都经过 \(x\)，即 \(xDx\)。
• 反对称性：若 \(xDy\)，\(yDx\)，则 \(1\rightsquigarrow y\) 的任意路径都经过 \(x\)。如果 \(x\neq y\)，那么存在 \(1\rightsquigarrow x\) 的路径不经过 \(y\)，和 \(yDx\) 矛盾。因此 \(x = y\)。反对称性 即对称性的反面：对称性要求对于任意 \(x\neq y\)，若 \(xDy\) 则 \(yDx\)。

满足以上三条性质的关系称为 偏序关系，元素集合和它对应的偏序关系一起称为偏序集。

补充

偏序关系的含义是 “部分” 满足 “序关系”，即局部满足 全序关系。在全序关系 \(R\) 里，元素两两可比较（对 \(x\neq y\)，\(xRy\) 或 \(yRx\) 恰有一个成立）。这种关系抽象成图是一排点，每个点指向它后面的所有点。

直观地，在一个偏序集内部，元素之间通过偏序关系形成很多条链，链与链之间有交叉。在交叉点以外，分别位于两个不同链的元素不能比较。但是单独取出某一条链，上面的元素形成全序集。

对偏序关系建图只能得到 DAG：如果环长大于 \(1\)，根据传递性，环上每个点向其它点连边，不满足反对称性。

性质 1

若 \(xDz\) 且 \(yDz\)，则 \(xDy\) 或 \(yDx\)。

证明

\(x = y\) 的情况显然。

因为 \(xDz\) 且 \(yDz\)，不妨设 \(x\) 在 \(y\) 之前，那么 \(y\) 不支配 \(x\)。如果在此基础上 \(x\) 不支配 \(y\)，那么存在一条 \(1\rightsquigarrow y\rightsquigarrow z\) 的路径不经过 \(x\)，与 \(xDz\) 矛盾。所以 \(xDy\)。\(\square\)

当一个偏序关系满足性质 1 时，就可以用树状结构刻画：考虑支配 \(z\) 的所有点 \(D_z = \{x_1, x_2, \cdots, x_k\}\)，对任意两个不同元素 \(x_i, x_j\) 应用该性质，可知元素之间形成了全序关系，所有 \(x_i\) 的关系可以用一条链描述。

设 \(idom_i\) 表示 \(D_i\) 去掉 \(i\) 之后被其它所有点支配的点，称为 \(i\) 的 直接支配点 (immediate dominator)。特别地，\(idom_s\) 没有定义。\(idom_i\) 可以理解为 \(i\) 的所有支配点当中除了 \(i\) 以外距离 \(i\) 最近的一个，这里 “最近” 是良定义的：类似无向图两点之间的必经点在它们之间的任意简单路径上出现顺序固定，有向图从起点到某一点之间的必经点在它们之间的任意简单路径上出现的顺序也是固定的。

从 \(idom_i\) 向 \(i\) 连边，得到 支配树 (dominator tree)，它是一棵叶向树。一个点在支配树上的祖先集合（包括它自己）恰为支配它的所有点。支配树刻画了有向图在给定起点时结点之间的必经关系，类似圆方树刻画了无向图上的必经关系。

4.2 有向无环图

DAG 无环的特殊性质使得我们能够方便地求出其支配树。

拓扑排序。设当前结点为 \(x\)。根据拓扑排序的性质，\(x\) 对拓扑序在它之前的结点的必经性没有影响，因为 \(x\) 不可达它们。因此，只需求出 \(idom_x\)。

当 \(x\) 只有一条入边 \(y\to x\) 时，显然 \(idom_x = y\)。到达 \(x\) 要走 \(y\to x\) 这条边，所以 \(y\) 支配 \(x\)，由支配的传递性推出 \(y\) 在支配树上的所有祖先 \(anc(y)\) 都是 \(x\) 的支配点，而 \(y\) 是距离 \(x\) 最近的一个。

当 \(x\) 有两条入边 \(y\to x\) 和 \(z\to x\) 时，若最后一条边是 \(y\to x\)，则集合 \(anc(y)\) 是必经点；若最后一条边是 \(z\to x\)，则集合 \(anc(z)\) 是必经点。据定义，\(x\) 的支配点是 \(anc(y)\) 与 \(anc(z)\) 的交集加上 \(x\)，前者即 \(anc(lca(y, z))\)。因此，\(idom_x = lca(y, z)\)。

根据上述分析，容易证明：若 \(x\) 有若干条入边 \(y_i \to x\)，则 \(anc(x) \backslash x\) 等于 \(\bigcap_{i = 1} ^ k anc(y_i)\)。所以

\[idom_x = lca(y_1, y_2, \cdots, y_k) \]

因为拓扑序在 \(x\) 之前的 \(idom\) 均已确定，所以在确定每个点的 \(idom\) 之后立刻预处理这个点的倍增数组，倍增求 LCA。时间复杂度 \(\mathcal{O}((n + m)\log n)\)。

模板题 代码。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1 << 16;
constexpr int K = 16;
constexpr int M = 1e6 + 5;
int p, topo[N], sz[N];
int n, dep[N], deg[N], anc[K][N];
int cnt, hd[N], nxt[M], to[M];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}
int lca(int u, int v) {
  if(!u || !v) return u | v;
  if(dep[u] < dep[v]) swap(u, v);
  for(int i = K - 1; ~i; i--) {
    if(dep[anc[i][u]] >= dep[v]) u = anc[i][u];
  }
  if(u == v) return u;
  for(int i = K - 1; ~i; i--) {
    if(anc[i][u] != anc[i][v]) {
      u = anc[i][u], v = anc[i][v];
    }
  }
  return anc[0][u];
}
int main() {
  cin >> n;
  for(int i = 1, u; i <= n; i++) {
    scanf("%d", &u);
    while(u) deg[i]++, add(u, i), scanf("%d", &u);
    if(!deg[i]) deg[i] = 1, add(n + 1, i);
  }
  queue<int> q;
  q.push(n + 1), dep[n + 1] = 1;
  while(!q.empty()) {
    int t = q.front();
    q.pop(), topo[++p] = t;
    dep[t] = dep[anc[0][t]] + 1;
    for(int i = 1; i < K; i++) anc[i][t] = anc[i - 1][anc[i - 1][t]];
    for(int i = hd[t]; i; i = nxt[i]) {
      int it = to[i];
      anc[0][it] = lca(anc[0][it], t);
      if(!--deg[it]) q.push(it);
    }
  }
  for(int i = p; i; i--) {
    int id = topo[i];
    sz[anc[0][id]] += sz[id] + 1;
  }
  for(int i = 1; i <= n; i++) printf("%d\n", sz[i]);
  return 0;
}

4.3 一般图

先考虑朴素做法。和无向图的必经性一样，我们删掉 \(x\) 后检查 \(s\) 是否可达 \(y\)，由此判断 \(x\) 是不是 \(y\) 的支配点。因此，独立地删掉每个点 \(x\neq s\)，剩余的图上所有 \(s\) 不可达的点被 \(x\) 支配。时间 \(\mathcal{O}(nm)\)。

Thomas Lengauer 和 Robert Tarjan 于 1979 年给出了更快的支配树算法。具体多快呢？\(\mathcal{O}(m\log n)\)。精细实现可以做到几乎线性的 \(\mathcal{O}(m\alpha(m, n))\)。

首先求出以 \(s\) 为根的 DFS 树，将每个点重新编号为它的时间戳。因为可以只走树边，所以每个点的直接支配点是它在树上的真祖先（祖先且不相等）。

引理 1

\(idom_x \neq x\) 且 \(idom_x\) 是 \(x\) 的祖先。

在研究强连通分量横叉边的性质的时候，一个基本结论是如果 \(v < u\)，那么 \(v\) 可达 \(u\) 当且仅当 \(v\) 可达 \(d\)，其中 \(d = lca(u, v)\)。接下来的引理和这个结论密切相关。

引理 2

如果 \(v < u\)，那么所有 \(v\) 到 \(u\) 的路径都经过 \(d\) 的祖先。

证明

在考虑 DFS 树的时候，一个形象的方法是把儿子按 DFS 顺序从左到右排列。这样，对于两个没有祖先后代关系的点，左边的点的时间戳小于右边的点。

这个引理的一句话证明是，因为只有树边或前向边增加编号，所以从小于 \(u\) 的点走到不小于 \(u\) 的点这一步 \(x\to y\) 是树边或前向边，那么 \(x\) 是 \(u\) 的祖先（如果 \(x < u\) 且 \(x\) 不是 \(u\) 的祖先，那么 \(x\) 子树内所有点都小于 \(u\)），而从 \(v\) 开始走到某个 \(u\) 的祖先的过程中，\(u, v\) 的 LCA 只会不断变浅。

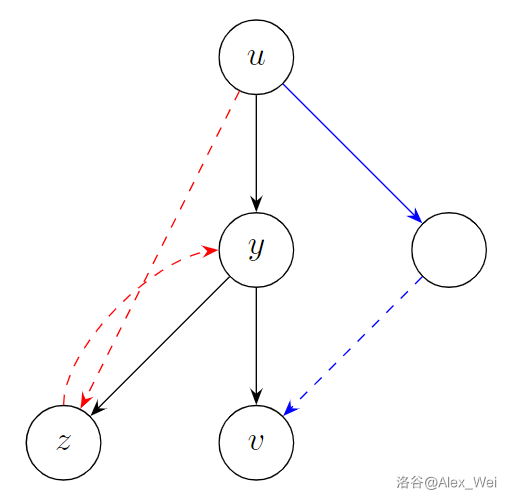
如上图，\(v = 6\)，\(u = 7\)，虚线是非树边。从 \(u\) 走到某个 \(d = 5\) 的祖先 \(1\) 之前的路径用红色标出，之后的路径用蓝色标出。绿色是编号大于 \(u\) 的点，可以发现能够直接走到它们的编号不大于 \(7\) 的点只有 \(7\) 的祖先。红色路径上每个点和 \(7\) 的 LCA 依次是 \(5, 1, 1\)，这个 LCA 只会变得越来越浅。

具体地，设 \(c\) 是当前 \(u\) 和 \(v\) 的 LCA，初始为 \(d\)，当 \(v = c\) 时停止。从 \(v\) 出发依次考虑路径上的每一步：

• 如果走树边或前向边，那么 \(c\) 不变。
• 如果走返祖边且没有停止，那么 \(c\) 不变。
• 如果走横叉边，那么 \(c\) 只会变成 \(c\) 的祖先，因为能够使得 \(c\) 变深的 \(v' > v\)，但横叉边只会减小时间戳。例如上图中不会出现 \(2, 3\) 或 \(4\) 到 \(6\) 的使得和 \(7\) 的 LCA 变深的横叉边。

所以最终的 \(c\) 是 \(d\) 的祖先，路径一定经过 \(d\) 的祖先。\(\square\)

引理 2 是有向图上路径的强有力而不那么平凡的结论。它可以想象成一个单向的 “屏障”，从 \(x\) 左边到 \(x\) 右边必须要经过这个屏障上的点，从 \(x\) 右边到 \(x\) 左边则不需要。

考虑 \(1\) 到 \(x\) 的任意路径。如果经过了小于 \(x\) 但不是 \(x\) 的祖先的点，那么根据引理 2，之后一定会经过 \(x\) 的祖先。我们考虑最后一个这样的祖先 \(d\)，之后只会经过大于 \(x\) 的点到 \(x\)。因此，\(d\) 可以只经过大于 \(x\) 的点到 \(x\)。如果有很多个这样的祖先，显然只有最浅的祖先对支配关系是有用的。这个概念比较关键，我们给它一个定义：

半支配点

存在路径 \(u\to p_1 \to \cdots \to p_k \to x\) 且 \(p_i > x\) 的最小的 \(x\) 的祖先 \(u\) 称为 \(x\) 的 半支配点 (semidominator)，记为 \(sdom_x\)。

将上述定义的 “\(x\) 的祖先” 的限制去掉没有影响，因为如果 \(u < x\) 且 \(u\) 不是 \(x\) 的祖先，那么根据引理 2，路径经过 \(x\) 的祖先 \(d < u\)。

为方便描述，对 \(u < v\)，我们称 \(u\) 到 \(v\) 的路径是 好路径，当且仅当中途只经过大于 \(v\) 的点。

已知 \(idom_x\) 和 \(sdom_x\) 都是 \(x\) 的祖先，那么自然地，我们希望确定它们的位置关系。这个也很显然：因为 \(sdom_x\) 可以绕过 \(sdom_x\) 到 \(x\) 的树上路径到达 \(x\)，所以这段路径上的点（不含 \(sdom_x\)）都不可能支配 \(x\)。

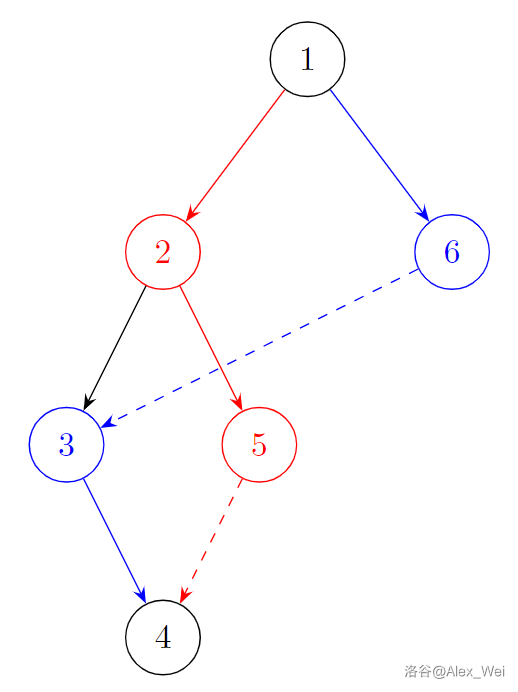
如上图，\(sdom_4 = 2\)，\(idom_4 = 1\)。\(3\) 不可能是支配点，因为根据 \(sdom\) 的定义，存在一条 \(2\) 到 \(4\) 且中途只经过大于 \(4\) 的点的路径 \(2\to 5\to 4\) 绕过了它。但是从 \(1\) 出发又可以绕过 \(2\) 到 \(4\)，所以 \(2\) 也不是支配点。

引理 3

\(idom_x\) 是 \(sdom_x\) 的祖先。

引理 3 可以理解为 \(sdom_x\) 到 \(x\) “跳过” 了一些点，这些点不可能成为 \(x\) 的支配点。引理 3 带给我们的启发是任何这样的 \((sdom_u, u)\) 二元组都能够让我们 “跳过” 一些点。

具体地，\(idom_x\) 和 \(sdom_x\) 都在 \(x\) 到根的路径上。我们把这条链拿出来水平摆放，\(1\) 在最左边，\(x\) 在最右边，那么每个 \(sdom_u\) 到 \(u\)（\(u\) 在链上）都会跳过一些点，这些点不可能是 \(x\) 的支配点，因为可以从 \(1\) 在链上走到 \(sdom_u\)，然后根据 \(sdom\) 的定义只经过大于 \(u\) 的点（于是不经过被跳过的点）到 \(u\)，再从链上走到 \(x\)。

以上分析表明被二元组跳过的点一定不是支配点。那么没有被任何二元组跳过的点是否一定是支配点呢？

引理 4

对 \(x\) 的真祖先 \(y\)，如果不存在 \(x\) 的祖先 \(u\) 使得 \(y\) 落在 \(sdom_u\) 到 \(u\) 在树上的路径上（不含两端），那么 \(y\) 支配 \(x\)。

证明

假设存在 \(1\) 到 \(x\) 的不经过 \(y\) 的路径。考虑路径上所有 \(x\) 的祖先，可知存在 \(u\) 到 \(v\) 的路径 \(P\)，使得路径上不经过其它 \(x\) 的祖先，其中 \(u, v\) 都是 \(x\) 的祖先且 \(u\) 是 \(y\) 的真祖先，\(v\) 是 \(y\) 的真后代。

假设 \(P\) 中途经过了小于 \(v\) 的点，那么根据引理 2，\(P\) 在此之后经过了 \(v\) 的真祖先，和 \(P\) 不经过其它 \(x\) 的祖先矛盾。于是 \(P\) 是好路径。因此 \(sdom_v \leq u\)。因为 \(u\) 是 \(y\) 的真祖先，所以 \(sdom_v\) 是 \(y\) 的真祖先，和 \(y\) 不落在任何 \(sdom_u\) 到 \(u\) 之间矛盾。\(\square\)

如上图，蓝色是从 \(u\) 出发跳过 \(y\) 的好路径，红色是从 \(u\) 出发经过 \(z < v\) 所以最终一定经过 \(lca(z, v)\)（\(x\) 的小于 \(v\) 的祖先）的路径。

引理 3 和引理 4 合起来告诉我们一个重要结论：\(y\) 支配 \(x\) 当且仅当 \(y\) 没有被覆盖。具体地，用 \(x\) 的所有祖先 \(u\) 的 \(sdom_u\) 到 \(u\)（不含两端）覆盖 \(1\) 到 \(x\) 的链，那么最深的没有被覆盖的 \(x\) 的真祖先就是 \(idom_x\)。这个显然可以 DP。

• 一个等价表述是仅保留树边和 \(sdom_x\) 到 \(x\) 的边不影响支配关系。于是可以使用 DAG 支配树的做法。

设 \(sdom_x\) 到 \(x\) 从左到右分别覆盖了 \(p_1, \cdots, p_k\)。如果这些点的 \(sdom\) 都在 \(sdom_x\) 及其右边，那么 \(sdom_x\) 就没有被覆盖。否则 \(idom_x\) 在 \(sdom_x\) 左边。

称添加一个点 \(u\) 表示用 \(sdom_u\) 到 \(u\) 覆盖。考虑使得 \(sdom_{p_i}\) 最小的 \(p_i\)，那么在添加 \(p_{i + 1}, \cdots, p_k, x\) 时，只会影响到 \(sdom_{p_i}\) 及其右边。假设现在已经添加了 \(1\) 到 \(p_i\) 的每个点，那么此时最深的未被覆盖的 \(p_i\) 的真祖先 \(idom_{p_i}\) 在 \(sdom_{p_i}\) 或其左边，而添加 \(p_{i + 1}, \cdots, p_k, x\) 不会让 \(idom_{p_i}\) 被覆盖，且覆盖了 \(p_{i\sim k}\)。于是此时最深的未被覆盖的 \(x\) 的真祖先依然是 \(idom_{p_i}\)。综上所述：

结论 1

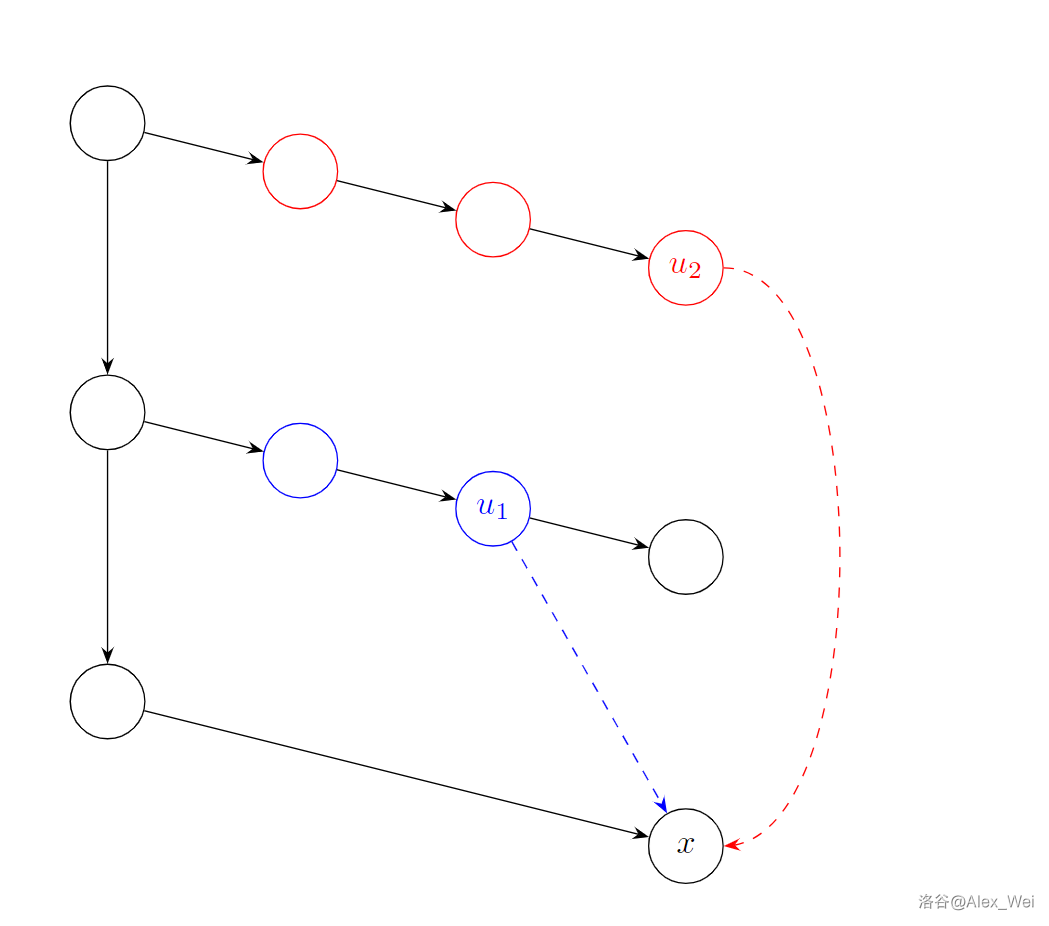
\[idom_x = \begin{cases} sdom_x, & \forall p_j : sdom_x \leq sdom_{p_j}; \\ idom_{p_i}, & \exists p_i :(\forall p_j : sdom_{p_i}\leq sdom_{p_j}) \land sdom_{p_i} < sdom_x. \end{cases} \]

如上图，红色的 \(idom_{p_i}\)（可能和 \(sdom_{p_i}\) 相等）不会被 \(p_j(j > i)\) 和 \(x\) 覆盖，而蓝色的 \(p_{i\sim k}\) 又被 \(x\) 覆盖，所以 \(idom_x = idom_{p_i}\)。

具体如何实现呢？只需计算 \(sdom_x\) 到 \(x\) 在树上的所有点（不含 \(sdom_x\)）的 \(sdom\) 的最小值。这种两端具有祖先后代关系的链上最值查询有很经典的做法：把查询挂到较浅的端点处，在 DFS 回溯时维护子树内每个点到当前点的链上最值并回答对应的询问，带权并查集即可。具体地，在并查集内额外维护每个点到它指向结点的树上路径的点权最小值，回溯时让当前点的所有儿子在并查集内指向当前点即可。

现在还要求 \(sdom\)。我们考虑从 \(u\) 到 \(x\) 的好路径。没有中间点的情况是容易处理的，因为此时 \(u\) 到 \(x\) 就是一条树边或前向边，只需求出指向 \(x\) 的 \(u\) 最小的前向边即可。

如果有中间点，那么根据 DP 的思想，自然地考虑路径的最后一条边 \(v\to x\)。但是这里有个问题，就是路径上 \(u\) 到 \(v\) 的部分不一定是好路径，而只用 \(sdom_v\) 更新 \(sdom_x\) 显然没有考虑到这种情况。

设中途经过的最小点是 \(y\)，那么 \(x < y \leq v\)。如果 \(y\) 不是 \(v\) 的祖先，那么根据引理 2，\(y\) 到 \(v\) 一定会经过 \(lca(y, v) < y\)，矛盾。因此 \(y\) 是 \(v\) 的祖先，也就是说，\(y\) 落在 \(lca(x, v)\) 到 \(v\) 在树上的路径上（不含 \(lca(x, v)\)）。而 \(y\) 又是中途经过的最小的点，所以路径上 \(u\) 到 \(y\) 的部分是好路径。

对于每条边 \(v\to x\)，考虑用 \(lca(x, v)\) 到 \(v\) 在树上的所有点（不含 \(lca(x, v)\)）的 \(sdom\) 更新 \(sdom_x\)。因为任何 \(u\) 到 \(x\) 的最后一条边是 \(v\to x\) 的好路径，都给出了 \(u\) 到 \(y\) 的好路径，所以不会漏情况，把 \(sdom_x\) 算大。而任何 \(u\) 到 \(y\) 的好路径都可以扩展（从树边走到 \(v\)，再走 \(v\to x\)）得到一条 \(u\) 到 \(x\) 的好路径，所以不会多情况，把 \(sdom_x\) 算小。

结论 2

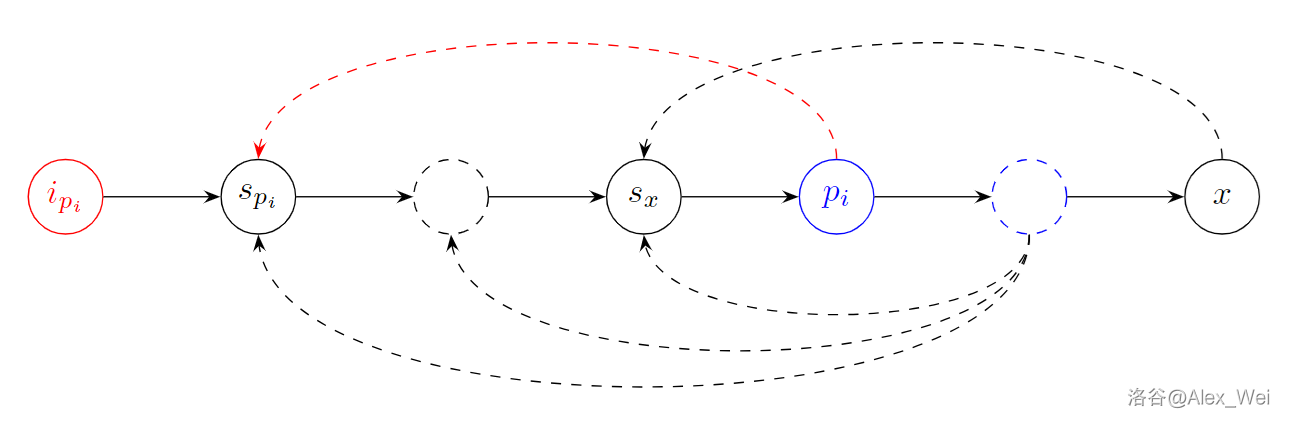
\[sdom_x = \min(\{u \mid u < x \land (u, x) \in E\} \cup \{sdom_y \mid y > x \land \exists u : (y\in anc(u) \land (u, x) \in E\})) \]

其中 \(anc(u)\) 表示 \(u\) 的祖先集合。

如上图，蓝色边 \(u_1\to x\) 对应的 \(y\) 用蓝色标出，红色边 \(u_2\to x\) 对应的 \(y\) 用红色标出。

后半部分怎么算呢？和 \(idom\) 一样，依然是具有祖先后代关系的链最值查询，使用带权并查集维护即可。不过显然地，这两部分可以共用一个带权并查集。

时间复杂度是并查集 \(n\) 次合并 \(m\) 次查询。模板题 代码。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e5 + 5;
int n, m, dn, fa[N], ind[N], dfn[N];
int sdom[N], idom[N], sz[N];
vector<int> e[N], rev[N], buc[N];
void dfs(int id) {
  ind[dfn[id] = ++dn] = id;
  for(int it : e[id]) if(!dfn[it]) fa[it] = id, dfs(it);
}
struct dsu {
  int fa[N], mi[N]; // mi 维护 sdom 最小的点的编号
  int find(int x) {
    if(fa[x] == x) return fa[x];
    int f = fa[x];
    fa[x] = find(f);
    if(sdom[mi[f]] < sdom[mi[x]]) mi[x] = mi[f];
    return fa[x];
  }
  int get(int x) {
    return find(x), mi[x];
  }
} tr;
int main() {
  cin >> n >> m;
  for(int i = 1; i <= m; i++) {
    int u, v;
    cin >> u >> v;
    e[u].push_back(v);
    rev[v].push_back(u);
  }
  dfs(1), sdom[0] = n + 1;
  for(int i = 1; i <= n; i++) tr.fa[i] = i;
  for(int i = n; i; i--) { // i = 1 的时候有些语句不用执行, 不过执行了也没事
    int id = ind[i];
    for(int it : buc[i]) idom[it] = tr.get(it); // 此时的 idom 是 sdom 最小的 pi
    if(i == 1) break;
    sdom[id] = i;
    for(int it : rev[id]) {
      if(dfn[it] <= i) sdom[id] = min(sdom[id], dfn[it]);
      else sdom[id] = min(sdom[id], sdom[tr.get(it)]);
    }
    tr.mi[id] = id, tr.fa[id] = fa[id]; // 连接 id 和 fa[id]
    buc[sdom[id]].push_back(id); // 把询问挂到对应位置
  }
  for(int i = 2; i <= n; i++) {
    int id = ind[i];
    if(sdom[idom[id]] != sdom[id]) idom[id] = idom[idom[id]]; // 如果 sdom 最小的 sdom[pi] 不等于 sdom[id], 那么 idom[id] = idom[pi]
    else idom[id] = sdom[id]; // 否则 idom[id] = sdom[id]
  }
  for(int i = n; i; i--) {
    int id = ind[i];
    sz[i] += 1;
    if(i > 1) sz[ind[idom[i]]] += sz[i];
  }
  for(int i = 1; i <= n; i++) cout << sz[i] << " ";
  cout << "\n";
  return 0;
}

CHANGE LOG

• 2022.5.26：修改文章。
• 2022.6.8：添加 SAT 的定义。
• 2022.6.10：添加 DAG 的支配树。
• 2022.9.30：添加 DAG 链剖分。
• 2023.7.6：移除同余最短路至 “图论 I”。
• 2024.8.13：添加无向图的耳分解。
• 2024.8.26：添加有向图的耳分解，双极定向。
• 2024.10.10：添加双极定向代码（P9394）。
• 2025.2.8：更新 2-SAT，添加一些图片。
• 2025.2.10：添加更简单的双极定向实现方法。
• 2025.2.13：添加一般图支配树，移除 DAG 链剖分至 “图论 III”。

参考资料

第一章

• 数理逻辑（2）：命题逻辑的等值、范式和推理演算 —— tetradecane。
• Conjunctive normal form —— Wikipedia。
• Boolean satisfiability problem —— Wikipedia。
• 算法学习笔记（71）：2-SAT —— Pecco。

第二章

• 【算法学习】圆方树 —— PinkRabbit。

第三章

• Ear decomposition —— Wikipedia。
• 2023 集训队论文《综述图论中连通性及相关问题的一些处理方法》—— 万成章。
• 双极定向的构造 —— Rainbow_sjy。

第四章

• Lengauer, Thomas; Tarjan, Robert Endre (July 1979). "A fast algorithm for finding dominators in a flowgraph".
• Partially ordered set —— Wikipedia。