【MATLAB习题】四杆机构的运动学参数求解
1.问题描述

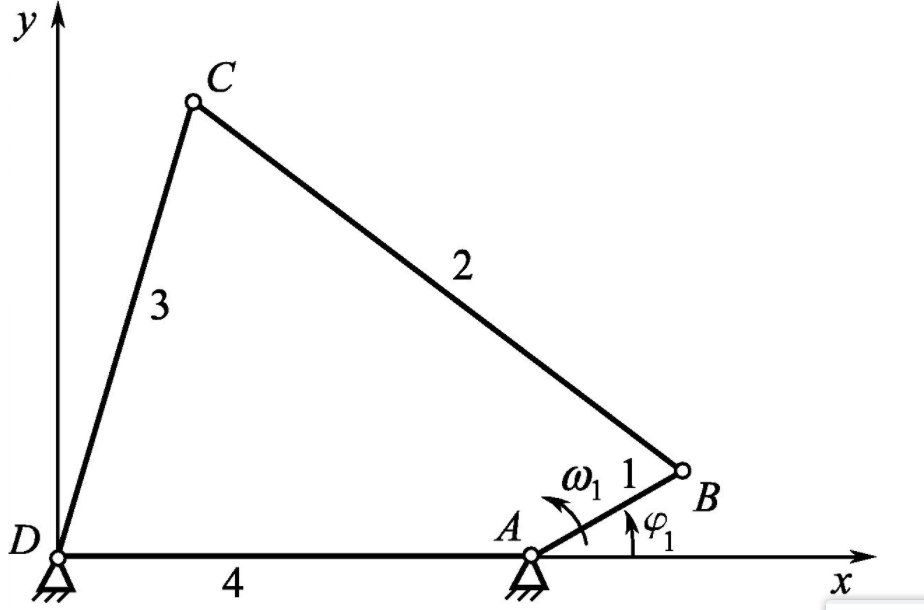
2. 推导过程



3. matlab代码
最新版代码
直接采用求微分的方式得到角度,角速度等数值解,速度慢,但是代码少,容易看懂(矩阵看起来真难受)。
以前做的一个博客文章用的是矩阵运算求解出线性方程组的方案,速度快,就是代码多一些。
%**********求解四杆机构的运动学参数***************
%1. 固定参数
l1=100 ;%单位:mm
l2=300;
l3=250;
l4=200;
w1=10.17;% rad/s
%定义角度单位换算
hd=pi/180;
jd=180/pi;
% 定义符号变量和有关的函数
syms lbd psi1
lbd(psi1)=sqrt(l4*l4+l1*l1-2*l4*l1*cos(pi-psi1));
syms theta1 theta2
theta1(psi1)= acos((l3*l3+lbd(psi1)*lbd(psi1)-l2*l2)/(2*l3*lbd(psi1)));
theta2(psi1)=asin((l1*sin(pi-psi1))/lbd(psi1));
%以上得到的结果均为弧度制
% psi3(psi1)=theta1+theta2;
% w3(psi1)=diff(psi3,psi1)*w1;
w3(psi1)=(diff(theta1,psi1)+diff(theta2,psi1))*w1;
i=1;
psi_1=zeros(1,73);
psi3=zeros(1,73);
w_3=zeros(1,73);
%循环求值
for n=0:5:360
%sin ,cos 函数是弧度制单位
psi_1(i)= n;
psi1=n*hd;
psi3(i)=theta1(psi1)+theta2(psi1);
w_3(i)=w3(psi1); %unit:rad/s
psi3(i)=psi3(i)*jd; %psi3转为角度制
i=i+1;
end
subplot(2,2,1);
plot(psi_1(:,1:73),psi3(:,1:73),'-b');
title('杆3的角度随\psi_1的变化曲线')
xlim([0 360])
xlabel('\psi_1 /\circ')
ylabel('\psi_3 / \circ')
grid on;
subplot(2,2,2);
plot(psi_1(:,1:73),w_3(:,1:73),'-r')
title('杆3的角速度曲线');
xlabel('角度')
xlim([0 360])
ylabel('角速度/rad\cdots^{-1}')
grid on;
subplot(2,2,[3 4])
[ax,h1,h2]=plotyy(psi_1,psi3,psi_1,w_3);
% 设置label
d1=get(ax(1),'ylabel');%取出左侧轴的ylabel句柄
set(d1,'string','角度值');%设置ylabel的值
d2=get(ax(2),'ylabel');%取出右侧轴的ylabel句柄
set(d2,'string','速度值');%设置ylabel的值
% 设置图例
legend([h1,h2],'角度','角速度');
%设置坐标轴刻度,范围
set(ax,'Xlim',[0 360],'xtick',[0:10:360])
history version
%**********求解四杆机构的运动学参数***************
%1. 固定参数
l1=100 ;%单位:mm
l2=300;
l3=250;
l4=200;
w1=10.17;% rad/s
%定义角度单位换算
hd=pi/180;
jd=180/pi;
% 定义符号变量和有关的函数
syms lbd psi1
lbd(psi1)=sqrt(l4*l4+l1*l1-2*l4*l1*cos(pi-psi1));
syms theta1 theta2
theta1(psi1)= acos((l3*l3+lbd(psi1)*lbd(psi1)-l2*l2)/(2*l3*lbd(psi1)));
theta2(psi1)=asin((l1*sin(pi-psi1))/lbd(psi1));
%以上得到的结果均为弧度制
i=1;
psi_1=zeros(1,74);
psi3=zeros(1,74);
psi2=zeros(1,74);
%循环求值
for n=0:5:360
%sin ,cos 函数是弧度制单位
psi_1(i)= n;
psi1=n*hd;
psi3(i)=theta1(psi1)+theta2(psi1);
psi2(i)=asin((l3*sin(psi3(i))-l1*sin(psi1))/l2);
psi2(i)=psi2(i)*jd; %弧度制转角度制
psi3(i)=psi3(i)*jd;
i=i+1;
end
plot(psi_1(:,1:73),psi3(:,1:73),'-b');
title('\psi_3')
xlim([0 360])
xlabel('\psi_1 /\circle')
ylabel('\psi_1&\psi-2 /\circ')
ylim([-360 360])
grid on;
hold on;
plot(psi_1(:,1:73),psi2(:,1:73),'-.r');
结果-速度图&角位移图
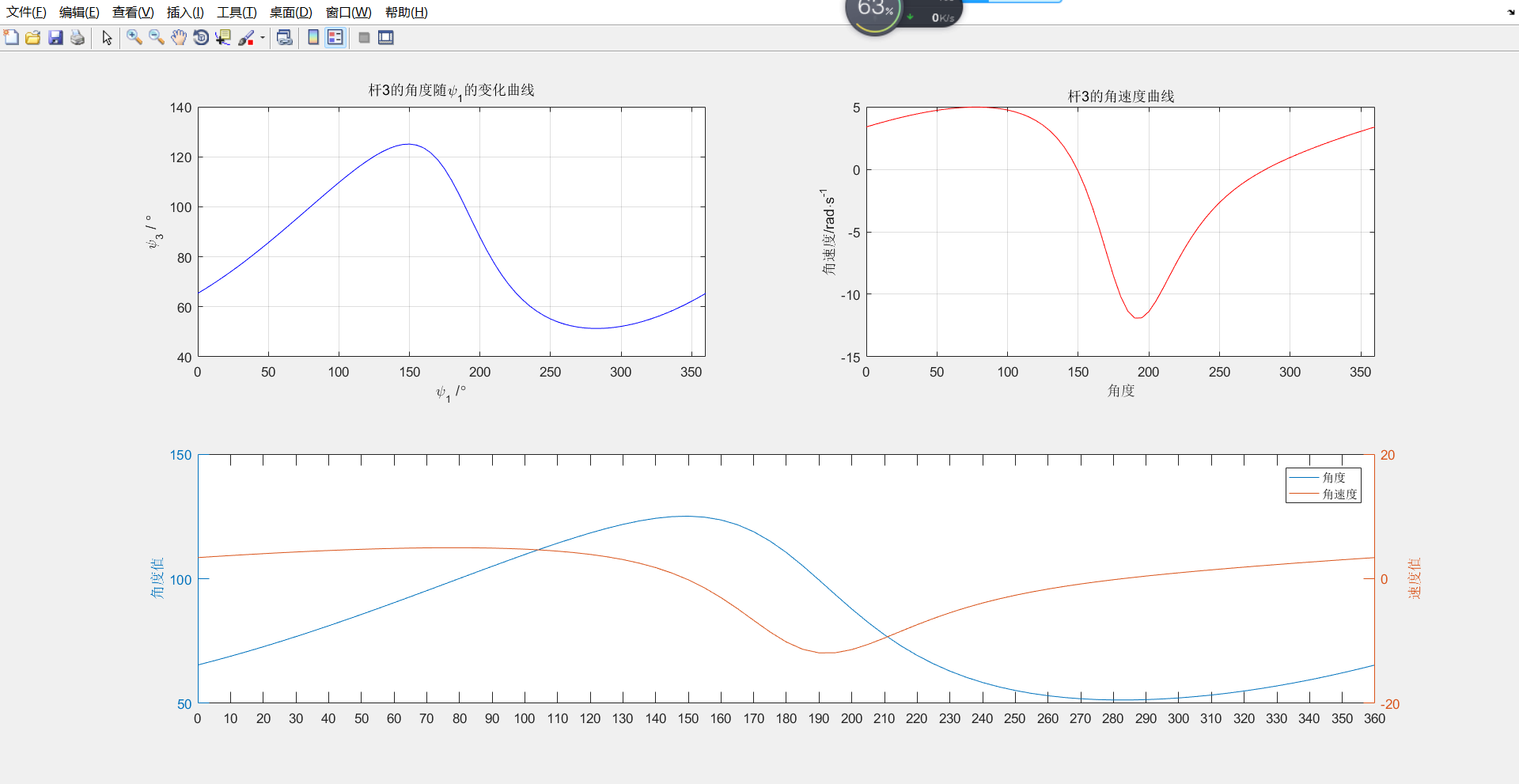
本文来自博客园,作者:FE-有限元鹰,转载请注明原文链接:https://www.cnblogs.com/aksoam/p/17013789.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号