P6186 [NOI Online #1 提高组] 冒泡排序

P6186 [NOI Online #1 提高组] 冒泡排序

分析

这题，我看了前几个题解，感觉跟我的写法都不太相同，所以我也说说我的写法。

首先我们需要探索一下每一轮冒泡排序会产生什么影响。

直接看一个例子就知道了。

原序列	5	3	6	1	2	4
数字对应的逆序数	0	1	0	3	3	2
原序列	3	5	1	2	4	6
数字对应的逆序数	0	0	2	2	1	0
原序列	3	1	2	4	5	6
数字对应的逆序数	0	1	1	0	0	0
原序列	1	2	3	4	5	6
数字对应的逆序数	0	0	0	0	0	0

我们，可以发现，每一次冒泡排序后，会把逆序数不为0的全部-1。

原因是因为冒泡排序的原理，对某一个数而言其若有逆序数，则其前面的最大的一个数一定会换到它后边，这样就会减少一个逆序数。

那我们如何将其利用到第二个操作中。

此时我们发现我们已经不在乎这些数在原序列中的哪些位置了，我们只在乎，这些数的逆序数是多少。

我们设f[i]表示i这个数在序列中的逆序数。

对于k轮冒泡排序而言，其会将使所有数的逆序数变为max(f[i]-k,0)

可能这样不太直观，我们来看看图。

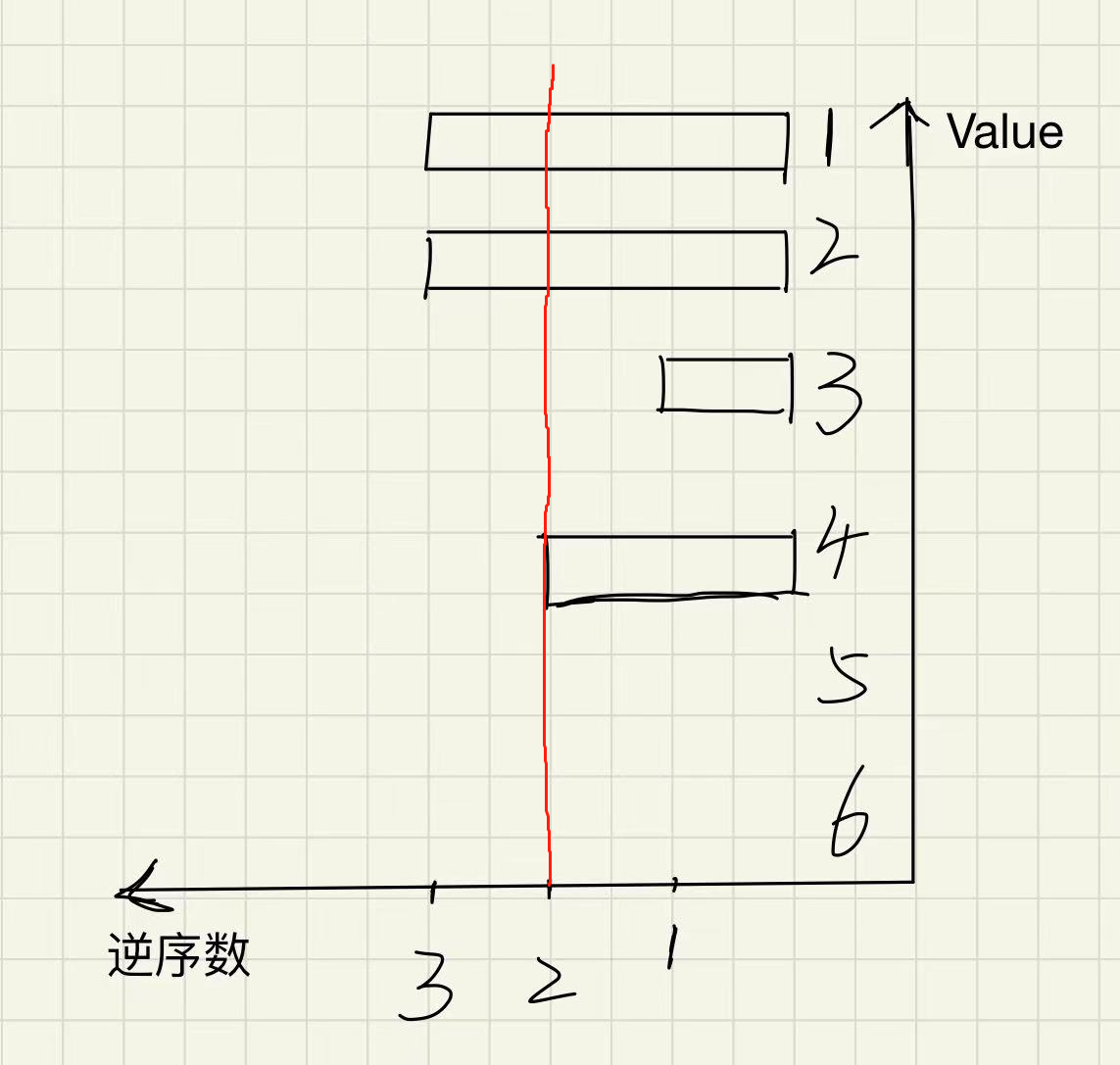
若我们假设k=2，则我们减掉的逆序对则为从逆序对的轴处画一条横直线，直线右边所有的柱子

这样是不是很像前缀和？因此，我们的思路在不带修的情况下是：

• 先求出对每一个值来说，其的逆序数。然后用一个桶记住每个值对应的逆序对数的数量。s[i]即表示对于逆序对数为i的值的数量
• 接下来直接对s[i]求前缀和。这样s[n]-s[i-1]就可以知道，大于等于i的值的个数。
• 则对于求具体某一轮操作i（i即为横坐标的逆序数）来说，其能减掉的逆序数，这个数就是所有逆序数大于等于i的值的数量，即为s[n]-s[i-1]。我们设为b[i]，即表示对于第i轮，会减掉的逆序对数
• 最后对b[i]求一个前缀和sum。当询问进行k轮时，则答案即为sum[n]-sum[k]。

但是，带修，我们该如何做呢？

我们先考虑交换相邻两个数的影响

• 若p[x]<p[x+1]，则交换后会使得p[x]的逆序数+1
• 若p[x]>p[x+1]，则交换后会使得p[x+1]的逆序数-1

这会影响，我们的前缀和数组，但我们不能每一次都求一边前缀和。因此不难想到，我们想动态求前缀和，则最好办法就是用树状数组解决问题啦。

接下来直接看代码吧。

Ac_code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int p[N],a[N],s[N];//p是原序列，a是每个值对应的逆序对数，s是初始的前缀和数组
LL tr1[N],tr2[N];//tr1是用来算初始逆序对的，tr2是用来动态算前缀和的
int n,m;

int lowbit(int x)
{
    return x & -x;
}

void add(LL tr[],int x,int c)
{
    while(x<=n)
    {
        tr[x] += c;
        x += lowbit(x);
    }
}

LL sum(LL tr[],int x)
{
    LL res = 0;
    while(x)
    {
        res += tr[x];
        x -= lowbit(x);
    }
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",p+i);
    for(int i=1;i<=n;i++)
    {
        add(tr1,p[i],1);
        int t = sum(tr1,n) - sum(tr1,p[i]);//对于p[i]而言其逆序数
        s[t] ++;//求出对每一个逆序对数，其有多少个
        a[p[i]] = t;//存一下每一个值的逆序对数
    }
    for(int i=1;i<=n;i++) s[i] += s[i-1];//对于每个i而言，其内有逆序对的数量
    for(int i=1;i<=n;i++) add(tr2,i,s[n]-s[i-1]);//求出对每个i而言，其能删掉的逆序对的数量。就是说逆序对数大于等于i的数量个数
    while(m--)
    {
        int op,x;scanf("%d%d",&op,&x);
        if(op==1)
        {
            if(p[x]<p[x+1]) 
            {
                a[p[x]]++;//p[x]这个值的逆序对数量+1
                add(tr2,a[p[x]],1);//+1后的值的位置+1
            }
            else 
            {
                add(tr2,a[p[x+1]],-1);//p[x+1]这个值的逆序对数的位置-1
                a[p[x+1]]--;
            }
            swap(p[x],p[x+1]);
        }
        else 
        {
            if(x>=n) puts("0");
            else printf("%lld\n",sum(tr2,n)-sum(tr2,x));//求大于x的部分的和。
        }
    }
    return 0;
}