P3178 [HAOI2015]树上操作

P3178 [HAOI2015]树上操作

分析

看题，是一道树剖+线段树裸题。不多说，贴一道板子P3384 【模板】轻重链剖分/树链剖分。这就可以解决这道题目了。

我们要说的是另外一种方法。

这里介绍一种不同于树剖的方法，首先需要知道一个概念：欧拉序，这是 DFS 序的一种，举个例子：

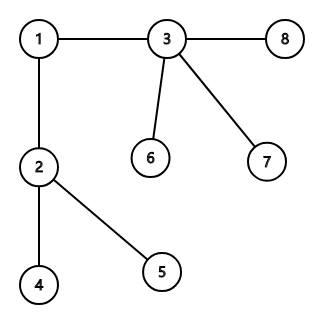
这样的一棵树，它的欧拉序为1 2 4 4 5 5 2 3 6 6 7 7 8 8 3 1

显然，每个点在欧拉序中出现了 2 次；欧拉序有一个非常优越的性质，如果把每个点第一次出现记作 +，第二次出现记作 -，那么根节点到任意节点的权值和在欧拉序上对应一个前缀和，这个性质非常好理解，因为欧拉序其实又叫"出栈入栈序"，所以前缀中尚未抵消掉的点在 DFS 到当前点时在栈中，那么其肯定在当前点到根的路径中。

我们分别来说如何利用欧拉序来完成三个操作

用dfn1表示结点第一次出现的欧拉序中的编号，dfn2表示结点第二次出现的欧拉序中的编号

操作一

把某个节点x的权值增加a

这个操作分为两个步骤，首先需要在线段树树上，第一次出现x的结点处+a，第二次出现x的结点处-a

我们加入一个数组num来统计从结点1开始到i中的+号的个数。

则，我们在进行修改操作的时候，对应结点处的符号可以直接通过num[i]-num[i-1]得到。

modify(1,dfn1[x],dfn1[x],c);
modify(1,dfn2[x],dfn2[x],c);

操作二

**把某个节点 x 为根的子树中所有点的点权都增加 a **

其中需要更改的是一个区间，那这个区间中有些节点需要+a，有些节点需要-a(因为子树中的结点被扫描的第一次和第二次结点标号都在区间中)。

那怎么办呢？

这时候我们只需要做一个小小的变化，其实一个区间受到 +a 的影响就是 \(a × (该区间内 + 的个数 - 该区间内 - 的个数)\)

modify(1,dfn1[x],dfn2[x],c);

操作三

询问某个节点 x 到根的路径中所有点的点权和。

这点就比较简单了。

直接上代码

query(1,1,dfn1[x])

AC_code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10,M = N*2;
struct Node
{
    int l,r;
    LL add,sum;
}tr[N<<3];
struct DfsNode
{
    int v,f;
}dfspath[N<<1];
int h[N],e[M],ne[M],w[N],idx;
int dfn1[N],dfn2[N],num[N<<1],ts;
int n,m;

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

void dfs(int u,int fa)
{
    dfn1[u] = ++ts,dfspath[ts].f = 1;
    dfspath[ts].v = u;
    for(int i=h[u];~i;i=ne[i])
    {
        int j = e[i];
        if(j==fa) continue;
        dfs(j,u);
    }
    dfn2[u] = ++ts,dfspath[ts].f = -1;
    dfspath[ts].v = u;
}

void pushup(int u)
{
    tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
}

void pushdown(int u)
{
    auto &root = tr[u],&left = tr[u<<1],&right = tr[u<<1|1];
    if(root.add)
    {
        left.add += root.add;
        left.sum += (num[left.r] - num[left.l-1])*root.add;
        right.add += root.add;
        right.sum += (num[right.r] - num[right.l-1])*root.add;
        root.add = 0; 
    }
}

void build(int u,int l,int r)
{
    if(l==r)
    {
        tr[u] = {l,r,0,dfspath[l].f*w[dfspath[l].v]};
        return ;
    }
    tr[u] = {l,r,0,0};
    int mid = l + r >> 1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
    pushup(u);
}

void modify(int u,int l,int r,int k)
{
    if(l<=tr[u].l&&tr[u].r<=r)
    {
        tr[u].add += k;
        tr[u].sum += 1ll*k*(num[tr[u].r]-num[tr[u].l-1]);
        return ;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if(l<=mid) modify(u<<1,l,r,k);
    if(r>mid) modify(u<<1|1,l,r,k);
    pushup(u);
}

LL query(int u,int l,int r)
{
    if(l<=tr[u].l&&tr[u].r<=r) return tr[u].sum;
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    LL res = 0;
    if(l<=mid) res += query(u<<1,l,r);
    if(r>mid) res += query(u<<1|1,l,r);
    pushup(u);
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    for(int i=0;i<n-1;i++)
    {
        int a,b;scanf("%d%d",&a,&b);
        add(a,b),add(b,a);
    }
    dfs(1,-1);
    for(int i=1;i<=ts;i++)
        num[i] = num[i-1] + dfspath[i].f;
    build(1,1,2*n);
    while(m--)
    {
        int op,x,c;scanf("%d%d",&op,&x);
        if(op==1)
        {
            scanf("%d",&c);
            modify(1,dfn1[x],dfn1[x],c);
            modify(1,dfn2[x],dfn2[x],c);
        }
        else if(op==2)
        {
            scanf("%d",&c);
            modify(1,dfn1[x],dfn2[x],c);
        }
        else cout<<query(1,1,dfn1[x])<<endl;
    }
    return 0;
}