AtCoder ABC 223 E

原题链接

分析

让我们先分析，两个矩形的情况、

不妨假设两个矩形的面积分别为S和T，如果我们想使两者不会发生覆盖，那我们可以轻松的得出两个结论

对于所有的满足该条件的放置，一定存在一条直线l，它平行于x或y轴，其满足:

• l不会经过任何一个矩形
• 可以将xy区间拆分为两部分，每一部分有一个矩形

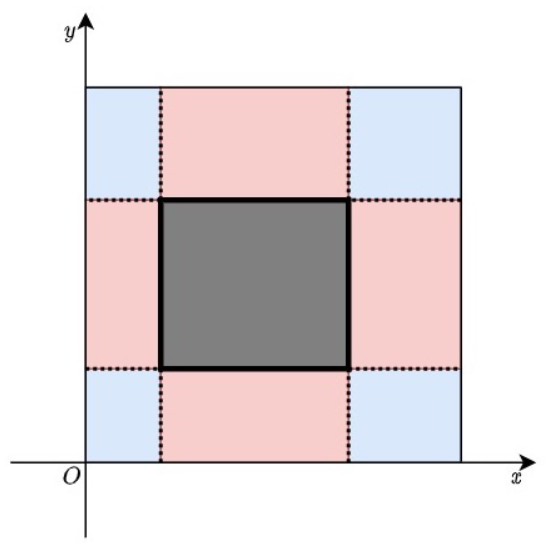
其中灰色部分是一个矩形S，则若需要找到另一个不发生覆盖的矩形T。T需要满足不会同时与两个红色部分有交集。

如果该直线l存在，且与x轴平行，则了l的取值\(y=\left \lceil \frac{S}{X}\right \rceil\)。

如果该直线l存在，且与y轴平行，则了l的取值\(x=\left \lceil \frac{S}{Y}\right \rceil\)。

接下来，我们来看一下三个矩形的情况、

就像两个矩形一样，我们也能证明以下两个结论、

对于所有的满足该条件的放置，一定存在一条直线l，它平行于x或y轴，其满足:

• l不会经过任何一个矩形
• 可以将xy区间拆分为两部分，其中一部分有一个矩形，另一部分有两个矩形。

第一步，任取两个矩形，取得l是满足分割两个矩形时的直线的。我们不妨设l为平行于y轴的直线。

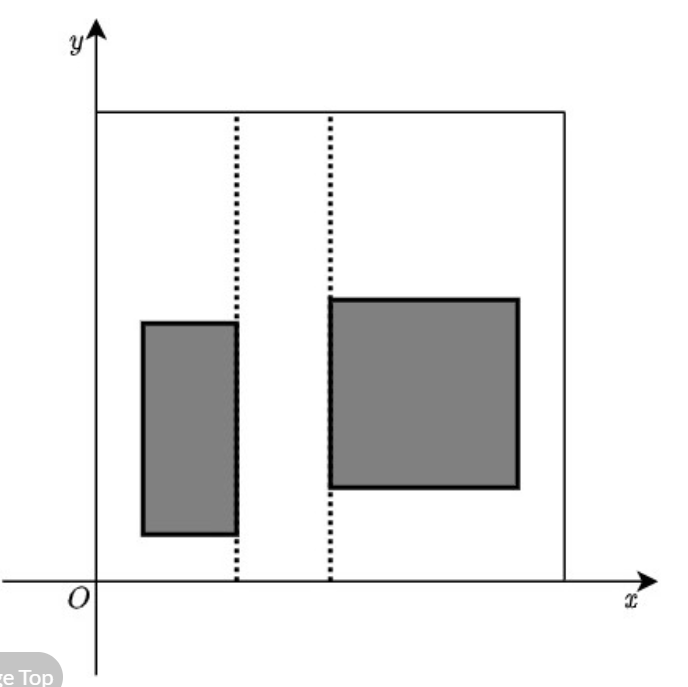
若，其中最多只有一条虚线经过最后一个矩形，则另一条虚线就可以作为分割线l

若同时经过两条虚线，则需要满足，蓝色区域与任意一个灰色区域都不相交。

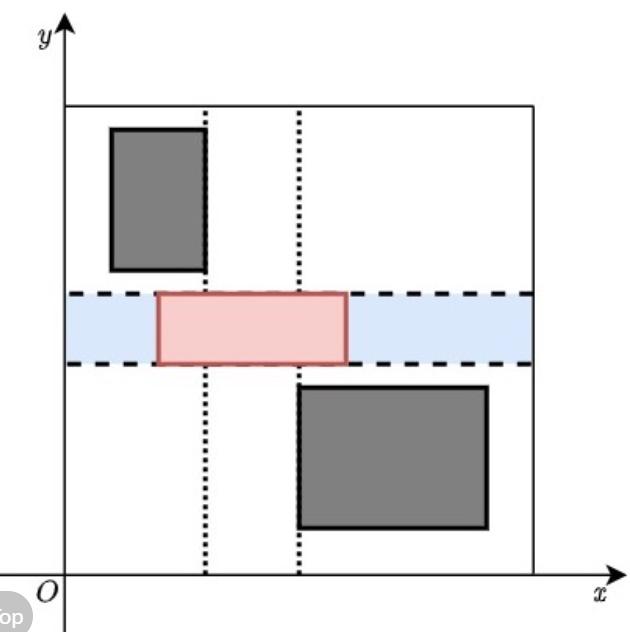
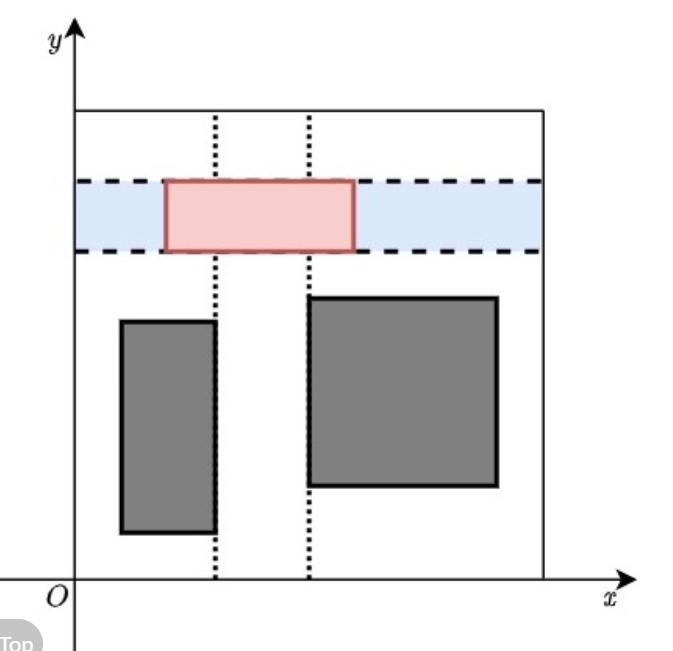
因此l需要满足的条件有

• l需要平行于x轴或y轴
• 同时，需要抉择，那一部分是有两个矩形的，解决那一部分的两个矩形时，可以用刚开始讨论的，两个矩形的情况。

Ac_Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

bool solve2(LL x,LL y,LL s,LL t)
{
    for(int i=0;i<2;i++){
        LL len = (s+x-1)/x;
        if(len<y&&x*(y-len)>=t){
            return 1;
        }
        swap(x,y);
    }
    return 0;
}

bool solve3(LL x,LL y,LL a,LL b,LL c){
    for(int i=0;i<2;i++){
        for(int j=0;j<3;j++){
            LL len = (a+x-1)/x;
            if(len<y&&solve2(x,y-len,b,c))
                return 1;
            swap(a,b);
            swap(b,c);
        }
        swap(x,y);
    }
    return 0;
}

int main()
{
    LL x,y,a,b,c;
    cin>>x>>y>>a>>b>>c;
    cout<<(solve3(x,y,a,b,c)?"Yes":"No")<<endl;
    return 0;
}