stereoRectify中的 P1 P2是将世界坐标系转到了什么坐标系
在OpenCV的stereoRectify函数中,输出的投影矩阵P1和P2将世界坐标系转换到了校正后的相机坐标系,具体来说是:
-
坐标系转换流程:
- 原始世界点 (X,Y,Z)
- 通过
P1/P2→ 校正后的相机坐标系 (u,v,w)
-
关键特性:
P1(左相机)和P2(右相机)是3×4投影矩阵- 它们已经包含了立体校正(rectification)的旋转矩阵R
- 输出坐标系的x轴与基线平行(极线水平对齐)
-
数学表示:
[u, v, w]^T = P * [X, Y, Z, 1]^T其中:
u/w和v/w得到校正后的像素坐标w实际上等于校正后坐标系中的Z值
-
与传统投影矩阵的区别:
- 普通投影矩阵:世界→原始像素坐标系
P1/P2:世界→校正后的像素坐标系- 包含了双目系统的基线信息(
P2的第4列包含Tx/f)
典型场景中,如果用reprojectImageTo3D计算视差图的三维坐标,得到的点云已经是校正后坐标系下的表示。如果需要原始相机坐标系的点云,需要应用校正旋转矩阵的逆变换。
建议使用时注意:
- 这个坐标系以左相机光心为原点
- X轴向右,Y轴向下,Z轴向前
- 极线完全水平对齐,便于立体匹配
用reprojectImageTo3D计算视差图的三维坐标XYZ后,我想将XYZ转换回相机坐标系,怎么计算?
要将 reprojectImageTo3D 计算出的三维坐标(校正后坐标系)转换回原始相机坐标系,需明确以下关键点并分步操作:
1. 坐标系关系
- 校正后坐标系 (
X_rect, Y_rect, Z_rect):
由reprojectImageTo3D(disparity, Q)直接得到,已通过立体校正旋转(R1/R2)对齐极线。 - 原始相机坐标系 (
X_cam, Y_cam, Z_cam):
校正前的相机坐标系,Z轴指向光轴方向。
二者的关系为:
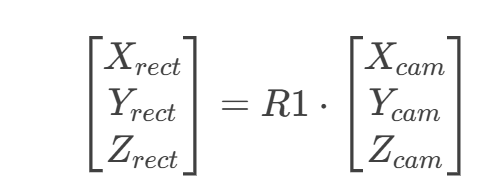
其中 R1 是 stereoRectify 返回的左相机校正旋转矩阵。
2. 转换步骤
方法一:直接逆旋转
import numpy as np
import cv2
# 假设已通过 stereoRectify 获取 R1, R2, P1, P2, Q
points_3d_rect = cv2.reprojectImageTo3D(disparity_map, Q) # 校正后坐标系
# 转换为原始左相机坐标系
R1_inv = cv2.Rodrigues(R1)[0].T # R1的逆矩阵(旋转矩阵的转置)
points_3d_cam = np.einsum('ij,hwj->hwi', R1_inv, points_3d_rect) # 批量矩阵乘法
方法二:从 Q 矩阵推导

可直接从视差 d 和像素坐标 (u,v) 计算原始相机坐标,无需显式使用 R1。
3. 验证方法
-
投影一致性检查
将转换后的(X_cam, Y_cam, Z_cam)用原始相机内参矩阵K投影,应得到原始图像坐标:# 假设 K 是原始相机内参矩阵 point_cam = np.array([X_cam, Y_cam, Z_cam]) projected = K @ point_cam projected /= projected[2] # 齐次坐标归一化 print("投影像素坐标:", projected[:2]) # 应与原始匹配点一致 -
深度方向验证
确保Z_cam为正且符合实际场景尺度(如人脸检测中典型值 0.5~2米)。
4. 注意事项
- 旋转矩阵的维度:
R1是 3x3 矩阵,需确保与坐标点乘法维度匹配。 - 右相机坐标系:
若需转到右相机坐标系,需额外减去基线平移T(来自stereoRectify):points_3d_cam_right = (cv2.Rodrigues(R2)[0].T @ points_3d_rect.T).T - T - 单位统一:
确保Q中的Tx与相机标定的物理基线一致(毫米/米)。
总结
-
核心公式:
![image]()
-
推荐方法:
直接对reprojectImageTo3D的结果左乘R1的逆矩阵(R1.T),简单高效。 -
应用场景:
后续处理(如目标检测、SLAM)通常需要原始相机坐标系下的点云。
reprojectImageTo3D(disparity, Q)得到的XYZ是世界坐标吗?
reprojectImageTo3D(disparity, Q) 返回的三维坐标 (X, Y, Z) 既不是世界坐标系,也不是原始相机坐标系,而是校正后的左相机坐标系下的坐标。以下是关键解析:
1. 坐标系本质
| 坐标系类型 | 说明 |
|---|---|
| 校正后左相机坐标系 | reprojectImageTo3D 的输出坐标系,原点在左相机光心,但坐标轴经过立体校正旋转(极线对齐) |
| 原始左相机坐标系 | 校正前的相机坐标系,Z轴沿光轴方向 |
| 世界坐标系 | 用户定义的全局坐标系,需通过相机外参(R, t)转换得到 |
2. 坐标转换关系
(1)校正后坐标 → 原始相机坐标
通过校正旋转矩阵的逆变换:
import cv2
import numpy as np
# 假设已通过 stereoRectify 获取 R1 (左相机校正旋转矩阵)
points_3d_rect = cv2.reprojectImageTo3D(disparity, Q) # 校正后坐标 (X_rect, Y_rect, Z_rect)
R1_inv = cv2.Rodrigues(R1)[0].T # R1的逆矩阵
points_3d_cam = np.einsum('ij,hwj->hwi', R1_inv, points_3d_rect) # 原始左相机坐标
(2)原始相机坐标 → 世界坐标
需通过相机外参(旋转矩阵 R 和平移向量 t):
# 假设 R 和 t 是左相机的外参(从世界坐标系到相机坐标系)
R_world_to_cam = R # 3x3 旋转矩阵
t_world_to_cam = t # 3x1 平移向量
# 将点云转换到世界坐标系
points_3d_world = np.einsum('ij,hwj->hwi', R_world_to_cam.T, points_3d_cam - t_world_to_cam)
3. 关键区别
| 方法 | 输出坐标系 | 是否需要额外转换 |
|---|---|---|
reprojectImageTo3D |
校正后左相机坐标系 | 需用 R1 转原始相机坐标系 |
| 手动计算(Z=f*T/d) | 原始左相机坐标系 | 可直接用于后续处理 |
4. 为什么不是世界坐标?
- Q矩阵不包含世界坐标系信息:
Q仅包含立体校正参数(基线Tx、焦距f、主点(cx, cy)),无世界坐标系的外参(R,t)。 - 默认原点在左相机:
若未提供世界坐标系的外参,所有坐标均相对于左相机光心。
5. 验证方法
# 检查校正后坐标的X轴是否平行于基线(极线水平)
print("校正后坐标系中基线的方向:", R1 @ np.array([1, 0, 0])) # 应接近 [1, 0, 0]
# 验证Z_cam方向
test_point = np.array([0, 0, 1, 1]) # 假设Z=1米的点
projected = (P1 @ test_point.T).T # 投影到校正图像
projected /= projected[2] # 归一化
print("投影像素坐标:", projected[:2]) # 应与实际观测一致
总结
- ✅
reprojectImageTo3D输出的是校正后左相机坐标系,非世界坐标。 - 🔄 转原始相机坐标:左乘
R1.T(R1来自stereoRectify)。 - 🌍 转世界坐标:需额外应用相机外参
(R, t)的逆变换。 - ⚠️ 注意:若未标定世界坐标系,所有坐标均为相机相对坐标。



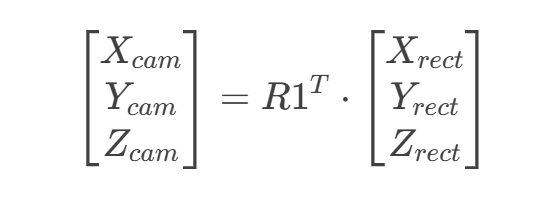

 浙公网安备 33010602011771号
浙公网安备 33010602011771号