四种字符串匹配算法（BF/KMP/BM/Sunday)

提示：点击右下角圆形按钮可开/关侧边目录，可开/关暗色模式。

本篇介绍几种常见字符串匹配算法，分别为

• BF算法（Brute Force，也就是暴力算法）
• KMP算法（Knuth-Morria-Pratt算法,其实就是这三个人共同提出的）
• BM算法（Boyer-Moore）
• Sunday算法（由Daniel M.Sunday在1990年提出）

Brute Force算法

也就是我们所谓的暴力算法。

顾名思义，假如有两个字符串：

• M（主串，也称文本串/被比较/m个字符）
• N（模式串/拿去比较/n个字符）

如图所示：
从左向右比较，开始时，若相同则M往后一位，N往后一位继续比，若不相同则M从第二位开始，N从第一位开始比较，依此类推。

BF算法的时间复杂度：
最坏时N的比较要循环m次，且每一位都要被比，因此最坏时间复杂度为O(n*m)

KMP算法

KMP算法用文字描述相当的不直观，需要不停地变化，因此这里我直接搬上我兄弟Carl的视频，讲的非常清楚，大家也可以关注一波。

---

理论篇

---

next函数构造篇

KMP的时间复杂度：
我们发现如果某个字符匹配成功，模式串首字符的位置保持不动，仅仅是i++、j++；如果匹配失配，i 不变（即 i 不回溯），模式串会跳过匹配过的next [j]个字符。整个算法最坏的情况是，当模式串首字符位于i - j的位置时才匹配成功，算法结束。

所以，如果文本串的长度为n，模式串的长度为m，那么匹配过程的时间复杂度为O(n)，算上计算next的O(m)时间，KMP的整体时间复杂度为O(m + n)。

BM算法

两个规则

坏字符规则：

• 当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。
• 此外，如果"坏字符"不包含在模式串之中，则最右出现位置为-1（不用管那么多，就是把模式串移到文本串不匹配字符的后面一位，待会儿会在图中展示）

好后缀规则：

• 当字符失配时，后移位数 = 好后缀在模式串中的位置 -好后缀在模式串上一次出现的位置。
• 如果好后缀在模式串中没有再次出现，则为-1。（和上文坏字符规则2一致）

例子

1.尾字符比较，坏字符S，且EXAMPLE里面没有S，故直接将模式串移到S后一位

2.尾字符比较，坏字符P，EXAMPLE里含P，故将模式串的P与文本串P对齐

3.尾字符比较，相同则向前继续比，会发现好后缀E，LE，PLE，MPLE，直至坏字符I，此时用好后缀规则，由于好后缀中只有E对应EXAMPLE的前缀，故将模式串的E与文本串中的E对齐

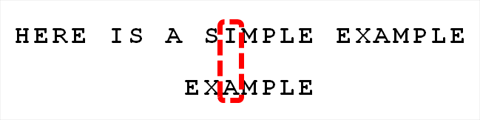
4.尾字符比较，坏字符P，同步骤2，后移匹配P，找到最终结果

Sunday算法

两个规则

• 如果该字符没有在模式串中出现则直接跳过，即移动位数 = 匹配串长度 + 1；
• 否则，其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。

例子

同样的例子

1.首字符比较，不一致，“坏字符”为空格，且模式串里不含空格，直接往后飞

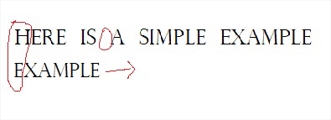
2.首字符比较，不一致，“坏字符”为E，模式串里存在E，取靠右的E与文本串里的E对齐

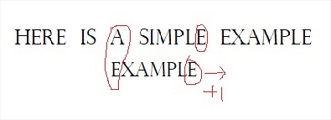
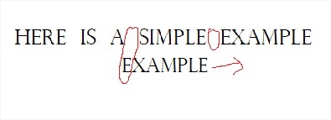
3.首字符比较，不一致，“坏字符”为空格，且模式串里不含空格，直接往后飞

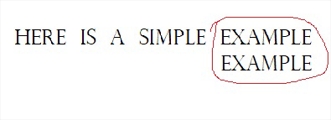
4.发现匹配,并可观察到Sunday算法比BM算法更快

总结

时间复杂度：

BF算法：最好O(m+n)，最坏O(mn)

KMP算法：O(m+n)

BM算法：最好O(n/m)，最坏O(mn)

Sunday算法：平均O(n)，最坏O(mn)，总体上来说Sunday优于BM算法

BF<KMP<BM<Sunday