AVL树

一：AVL树的概念

概念：
平衡二叉树也叫二叉搜索树又被称为AVL树，可以保证查询效率较高。它是一棵空树或者它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

二：AVL树左旋转思路

当右子树的高度比左子树高度大1时，进行左旋转。
首先假定一棵二叉树 [4，3，6，5，7，8]

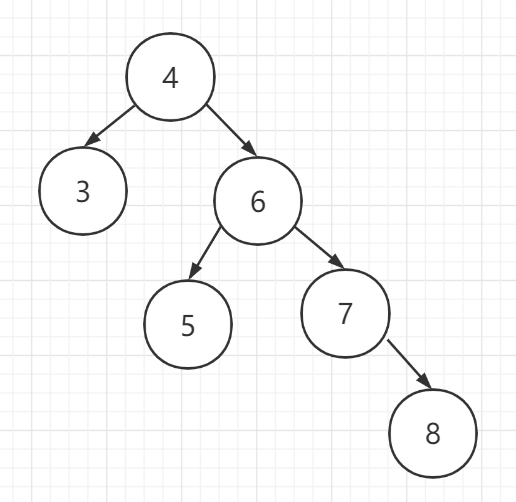
第一步：创建一个新的节点，值为当前根节点的值 【4】
第二步：将新节点【4】的左子树设置为当前节点【根节点】的左子树
第三步：把新节点【4】的右子树设置为当前节点【根节点】的右子树的左子树

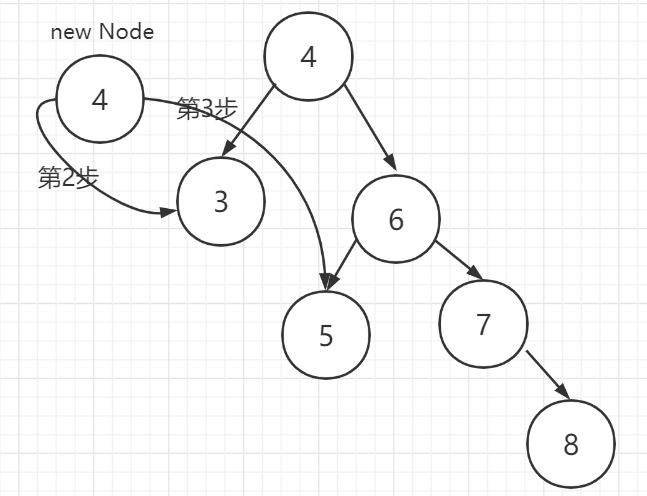
第四步：将当前节点【根节点】的值变为右子节点【6】的值
第五步：把当前节点【根节点】的右子树设置为右子树的右子树
第六步：将当前节点的左子树设置为新节点

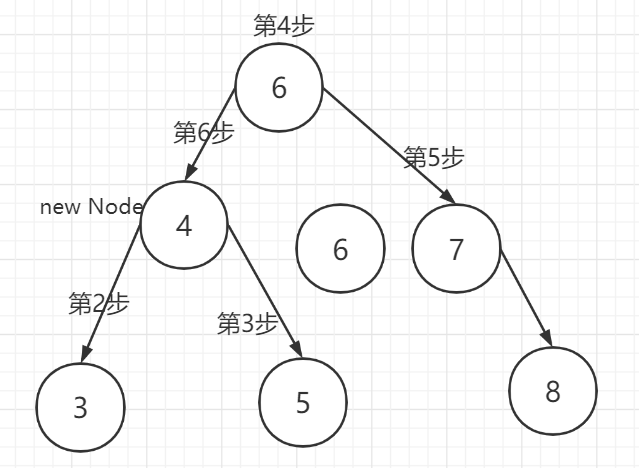
最终节点【6】被当作垃圾回收
在实现代码之前，我们需要知道的一个核心的操作：
我们需要知道左右子树的高度是多少，因为只有当左右子树的高度差大于1才需要进行旋转。
计算高度代码实现：

//返回左子树的高度
public int leftHeight(){
      if(left == null){
          return 0;
      }
    return left.height();
}
//返回右子树的高度
public int rightHeight(){
      if(right == null){
          return 0;
      }
    return right.height();
}
//返回以当前节点为根节点的高度
public int height(){
      return Math.max(left == null ? 0: left.height(), right == null ? 0: right.height())+1;
 }

左旋转方法代码

private void leftRotate(){

       //1.创建新的节点，值为根节点的值
       Node newnode = new Node(value);
       //2.将新节点的左子树设置为当前节点的左子树
       newnode.left = this.left;
       //3.将新节点的右子树设置为当前节点右子树的左子树
       newnode.right = this.right.left;
       //4.将当前节点的值设置为右子节点的值
       this.value = this.right.value;
       //5.将当前节点的右子树设置为右子树的右子树
       this.right = this.right.right;
       //6.将当前节点的左子树设置为新节点
       this.left = newnode;
}

三：AVL树右旋转思路

当左子树的高度比右子树的高度大1时，需要进行右旋转。
首先假定一棵二叉树 [10，12，8，9，7，6]

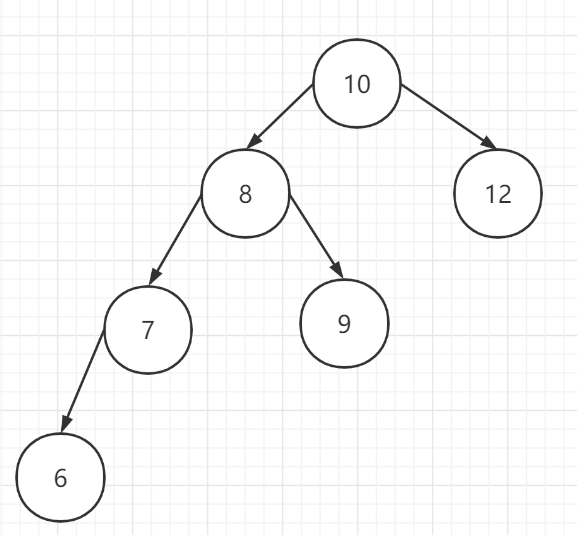
第一步：创建一个新的节点，值为当前根节点的值【10】
第二步：将新节点【10】的右子树设置为当前节点的右子树【12】
第三步：将新节点【10】的左子树设置为当前节点的左子树的右子树【9】

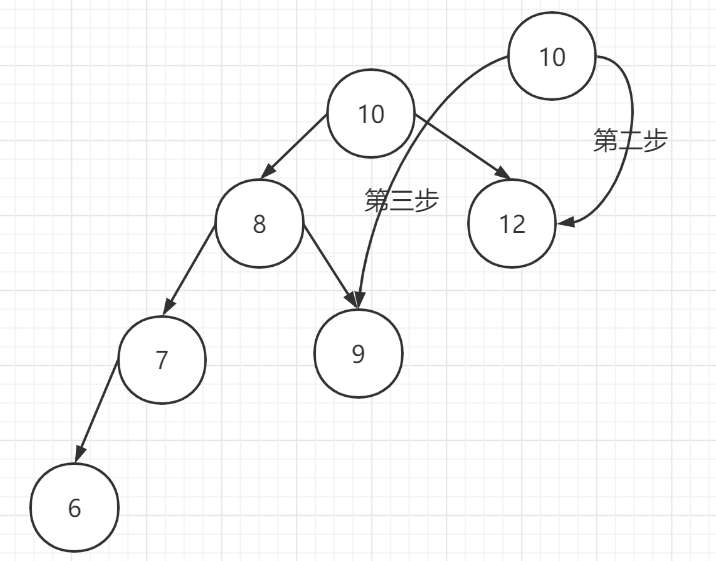
第四步：将当前节点【10】的值设置为左子节点【8】的值
第五步：将当前节点【8】的左子树设置为左子树的左子树【7】
第六步：将当前节点【8】的右子树设置为新节点【10】

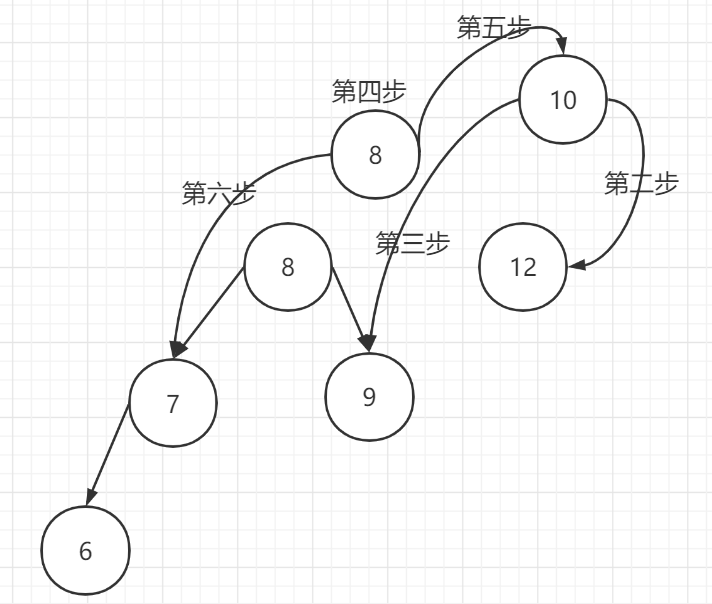
最后：节点【8】被当作垃圾回收

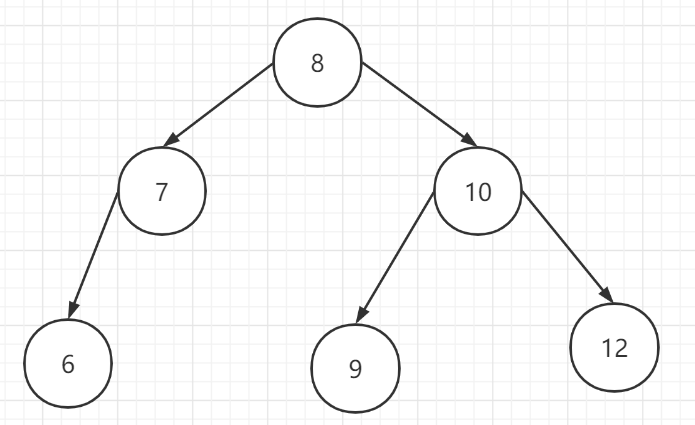
同样我们需要计算出左右子树的高度，代码与左旋转一样。
右旋转方法代码：

private void rightRotate(){

     //1.创建一个新的节点，值为当前根节点的值
         Node newNode = new Node(value);
     //2.将新节点的右子树设置为当前节点的右子树
         newNode.right = this.right;
     //3.将新节点的左子树设置为当前节点的左子树的右子树
         newNode.left = this.left.right;
     //4.将当前节点的值设置为左子节点的值
         this.value = this.left.value;
     //5.将当前节点的左子树设置为左子树的左子树
         this.left = this.left.left;
     //6.将当前节点的右子树设置为新节点
         this.right = newNode;
}

在上述两个数列中单旋转就可以将非平衡二叉树转成平衡二叉树，但是左/右旋转在某些情况下不能将非平衡树转成平衡树。比如：【10，11，7，6，8，9】那么这个时候就需要采用双旋转了。

四：AVL树双旋转思路

假定一棵二叉树 [10，11，7，6，8，9]

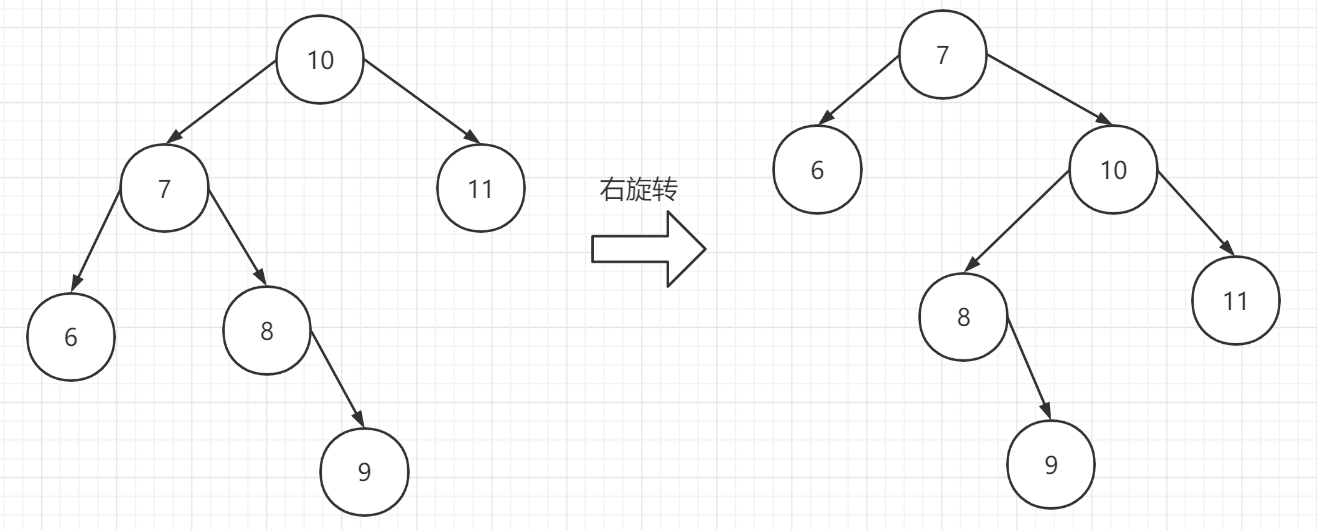
问题分析：
1.当前节点【10】的左子树的右子树的高度大于它的左子树的高度
解决方法：
1.首先对当前节点【10】的左子树进行左旋转
2.再对当前节点【10】进行右旋转即可
代码实现：

//添加完一个节点以后，如果(左子树的高度 - 右子树的高度) > 1，右旋转
if(leftHeight() - rightHeight() > 1){
    //判断它的左子树的右子树高度是否比左子树高
    if(left.rightHeight() > left.leftHeight()){
        //对当前结点的左子树进行左旋转
        left.leftRotate();
        //再进行右旋转
        rightRotate();
    }else{
        //直接进行右旋转
        rightRotate();
    }
    return;  //返回，防止进入下面的操作  
}

同理，另一种情况(右子树的左子树高度大于右子树的高度)
解决思路：
1.首先对当前节点的右子树进行右旋转
2.再对当前节点进行左旋转
代码实现：

//添加完一个节点以后，如果(右子树的高度 - 左子树的高度) > 1，左旋转
if(rightHeight() - leftHeight() > 1){
    //判断它的右子树的左子树高度是否比右子树高
    if(right.leftHeight() > right.rightHeight()){
        //对当前结点的右子树进行右旋转
        right.rightRotate();
        //再进行左旋转
        leftRotate();
    }else{
        //直接进行左旋转
        leftRotate();
    }
    return;
}

完。