考虑绿电与储能的供热流量日前优化分配案例:基于pyomo实现
问题描述
本案例在微电网日前优化调度基础上加以修改,其结构如下图所示。系统电力侧包含有风电、光伏、以及电网。
热力侧包含有热泵、储熱罐、电加热、以及相应的热负荷需求。日前经济调度调度问题是指在对风电出力、光伏出力、热负荷进行日前(未来24h)预测的基础上,充分消纳绿电为前提,考虑电网的分时电价,通过热泵与储熱罐等可调控手段,使得系统经济性最优。
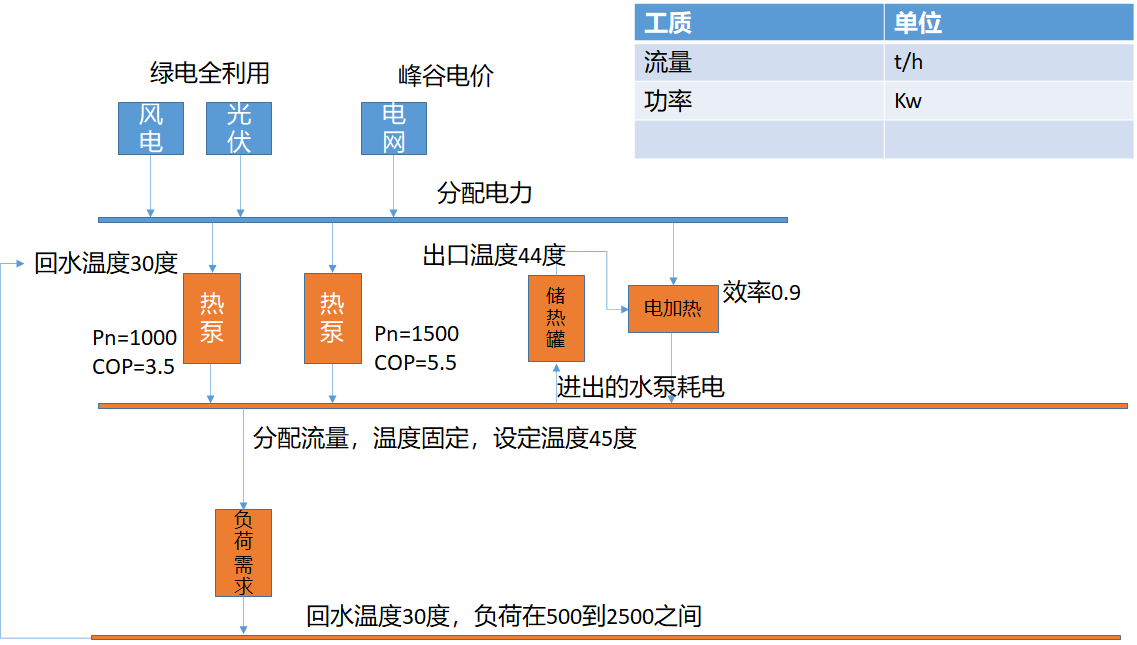
案例要求在如下已知条件下,求不同调度方案的平均用电成本
- 未来24h、每隔15min共96个时间点的负荷、光伏、风电出力预测,及分时电价数据;
- 两台热泵额定制热功率为 1000kw 和 1500kw,COP 分别为 3.5 和 5.5,负荷率不得低于 30%,15 分钟内负荷变化小于额定的 10%,设定热泵出口温度为 45 度。
- 储热罐容量为 1.5 吨,储热损失 1 度,储热罐容量百分比需要在 0.1 到 0.9 之间,初始在 0.2,要求调控时间周期结束后容量百分比不变。
- 电加热效率为 0.9,主要用于储热罐供热流量的再热。
- 储热罐流入与流出需要两台水泵,水泵扬程记为 2m,轴效率为 0.8,电效率因数 k=1.25。
- 需求侧回水温度为 30 度。
模型构建
案例涉及热泵、储热罐、电力侧和热力侧,我们依次建立数学模型,然后交予求解器求解。
一个基于 pyomo 的数学模型包含六大要素(决策变量,约束,目标函数,索引集合,参数,表达式)
- 索引集合:决策变量的索引,包含系统的时间索引和设备索引。
- 决策变量:水泵的流量和储热罐的进出水流量。
- 约束:能量平衡和流量平衡,以及各设备需要满足的参数要求。例如热泵的功率限制,储热罐的容量限制等。
- 目标函数:运行成本,即系统电费
- 参数、表达式:用于表示系统各项属性。
开始先抽象一个模型基类,表示各类调度设备,包含名称、资源上线、等基本属性,同时提供一个create_model()方法,用于实现决策变量、约束条件、目标函数等模型三要素。
class Model:
"""Model基类模型"""
def __init__(self, name: str,
Upper, # 资源上限
efficiency,# 使用能源时的效率
):
"""资源模型的基类"""
# technical parameters
self.name = name
self.Upper = Upper
self.efficiency = efficiency
def create_model(self, model, dt: float):
raise NotImplementedError
然后定义一个最后执行的优化函数。
其中利用pyo.ConcreteModel()定义模型。
设置表示时间点的索引集合。data中包含负荷需求序列与绿电出力序列。
pyo.Set(initialize=[i for i in range(len(data))])由于有 96 个时间点,所以此处设置长度为 96 的时间索引。
def optimize(data,resources):
model = pyo.ConcreteModel()
model.TimePoint = pyo.Set(initialize=[i for i in range(len(data))]) # 采用列表初始化集合索引,表示时间点
1、热泵模型
热泵模型继承自Model基类,同时新增了 回水温度与出水温度的属性。
在 create_model()方法中设定索引、决策变量、表达式、与约束。
1)定义索引
有两台热泵,所以定义长度为 2 的热泵设备 ID 索引,用于区分热本 1 与热泵 2。
model.pumpID = pyo.Set(initialize = [i for i in range(len(self.efficiency))])
2)决策变量
设置热泵的流量为决策变量,由时间索引与热泵设备 ID 索引可设置 96*2 的二维决策变量,同时设置下限为 0,上限暂时未定由约束给出。
model.Pump_M = pyo.Var(model.TimePoint,model.pumpID,
within=pyo.NonNegativeReals, bounds=(0,None))
3)表达式
热泵制热功率表达式:流量温差比热。考虑到单位转换后为M(OutT-InT)4.2*1000/3.6
def Pump_Q_rule(model,timestamp,id):
return (model.Pump_M[timestamp,id]*(self.OutT-self.InT)*4.2*1000/3.6)
model.Pump_Q = pyo.Expression(model.TimePoint,model.pumpID, rule=Pump_Q_rule)
热泵耗电表达式:制热功率/SOC
def Pump_P_rule(model,timestamp,id):
return model.Pump_Q[timestamp,id]/self.efficiency[id]
model.Pump_P = pyo.Expression(model.TimePoint,model.pumpID, rule=Pump_P_rule)
4)约束
# 约束
# 热泵制热功率限制,小于额定功率,大于额定功率的0.3,功率变化值小于额定的0.1
def Pump_Q_constr_rule1(model,timestamp,id):
return model.Pump_Q[timestamp,id] <= self.Upper[id]
model.Pump_Q_constr1 = pyo.Constraint(model.TimePoint,model.pumpID, rule = Pump_Q_constr_rule1)
def Pump_Q_constr_rule2(model,timestamp,id):
return model.Pump_Q[timestamp,id] >= 0.3*(self.Upper[id])
model.Pump_Q_constr2 = pyo.Constraint(model.TimePoint,model.pumpID, rule = Pump_Q_constr_rule2)
def Pump_Q_constr_rule3(model,timestamp,id):
if timestamp==0:
return pyo.Constraint.Skip
else:
return (model.Pump_Q[timestamp,id] - model.Pump_Q[timestamp-1,id]) <= 0.1*(self.Upper[id])
model.Pump_Q_constr3 = pyo.Constraint(model.TimePoint,model.pumpID, rule = Pump_Q_constr_rule3)
def Pump_Q_constr_rule4(model,timestamp,id):
if timestamp==0:
return pyo.Constraint.Skip
else:
return (model.Pump_Q[timestamp,id] - model.Pump_Q[timestamp-1,id]) >= -0.1*(self.Upper[id])
model.Pump_Q_constr4 = pyo.Constraint(model.TimePoint,model.pumpID, rule = Pump_Q_constr_rule4)
2、储热罐模型
def __init__(self, name: str,
Upper: float, # 储熱罐容量(吨)
efficiency: float, # 出口电加热效率
InT: float, # 进水温度
OutT: float,# 出口温度
init_soc: float, # 初始储水比例
soc_limit: list, # 储水比例可允许的范围(0.1-0.99)
新增了 进水温度与出水温度的属性和 初始储水比例以及储水比例可允许的范围(0.1-0.99)。
1)决策变量
储热罐有两个流量,一个流出一个流入,在此定义成两组变量,每组变量长度为 96。下限为 0,初始值为 0.
model.Stor_In_M = pyo.Var(model.TimePoint,within=pyo.NonNegativeReals, bounds=(0,None),initialize = 0)
model.Stor_Out_M = pyo.Var(model.TimePoint,within=pyo.NonNegativeReals, bounds=(0,None),initialize = 0)
2) 表达式
# 储熱罐水泵用电功率
def Stor_pump_P_rule(model,timestamp):
return ((model.Stor_In_M[timestamp] + model.Stor_Out_M[timestamp])*5*9.8*1.25/0.8)
model.Stor_pump_P = pyo.Expression(model.TimePoint, rule=Stor_pump_P_rule)
# 出水流量电加热 热能出力表达式
def Stor_Out_Q_rule(model,timestamp):
return (model.Stor_Out_M[timestamp]*(self.InT-self.OutT)*4.2*1000/3.6)
model.Stor_Out_Q = pyo.Expression(model.TimePoint, rule=Stor_Out_Q_rule)
# 出水流量电加热功率
def Stor_P_rule(model,timestamp):
return model.Stor_Out_Q[timestamp]/self.efficiency
model.Stor_P = pyo.Expression(model.TimePoint, rule=Stor_P_rule)
# SOC表达式
def StorageSOC_rule(model,timepoint):
soc = self.init_soc
delta = ( (model.Stor_In_M[timepoint]-model.Stor_Out_M[timepoint]) * dt) / self.Upper
if timepoint==0:
soc = soc + delta
else:
soc = model.Stor_soc[timepoint-1] + delta
return soc
model.Stor_soc = pyo.Expression(model.TimePoint, initialize=StorageSOC_rule)
3)约束
- 储热罐流入与流出只能有其一。
当采用 流入流量 * 流出流量 = 0 约束时,出现无法求解的情况。
def Stor_M_constr_rule(model,timestamp):
return model.Stor_In_M[timestamp]*model.Stor_Out_M[timestamp]==0
model.Stor_M_constr = pyo.Constraint(model.TimePoint, rule=Stor_M_constr_rule)
ValueError: Cannot load a SolverResults object with bad status: error
为此对约束进行松弛, 改为 (流入流量 - 流出流量)2 >=流入流量2 和 >= 流出流量**2
def Stor_M_constr_rule2_1(model,timestamp):
return (model.Stor_In_M[timestamp]-model.Stor_Out_M[timestamp])**2 >= model.Stor_In_M[timestamp]**2
model.Stor_M_constr2_1 = pyo.Constraint(model.TimePoint, rule=Stor_M_constr_rule2_1)
def Stor_M_constr_rule2_2(model,timestamp):
return (model.Stor_In_M[timestamp]-model.Stor_Out_M[timestamp])**2 >= model.Stor_Out_M[timestamp]**2
model.Stor_M_constr2_2 = pyo.Constraint(model.TimePoint, rule=Stor_M_constr_rule2_2)
- 流量变化限制约束:15 分钟内流量变化小于容量的 0.2
th = 0.2
def Stor_In_M_constr_rule1(model,timestamp):
if timestamp==0:
return pyo.Constraint.Skip
else:
return (model.Stor_In_M[timestamp] - model.Stor_In_M[timestamp-1]) <= th*self.Upper
model.Stor_In_M_constr1 = pyo.Constraint(model.TimePoint, rule = Stor_In_M_constr_rule1)
def Stor_In_M_constr_rule2(model,timestamp):
if timestamp==0:
return pyo.Constraint.Skip
else:
return (model.Stor_In_M[timestamp] - model.Stor_In_M[timestamp-1]) >= -th*self.Upper
model.Stor_In_M_constr2 = pyo.Constraint(model.TimePoint, rule = Stor_In_M_constr_rule2)
def Stor_Out_M_constr_rule1(model,timestamp):
if timestamp==0:
return pyo.Constraint.Skip
else:
return (model.Stor_Out_M[timestamp] - model.Stor_Out_M[timestamp-1]) <= th*self.Upper
model.Stor_Out_M_constr1 = pyo.Constraint(model.TimePoint, rule = Stor_Out_M_constr_rule1)
def Stor_Out_M_constr_rule2(model,timestamp):
if timestamp==0:
return pyo.Constraint.Skip
else:
return (model.Stor_Out_M[timestamp] - model.Stor_Out_M[timestamp-1]) >= -th*self.Upper
model.Stor_Out_M_constr2 = pyo.Constraint(model.TimePoint, rule = Stor_Out_M_constr_rule2)
- SOC 约束
s1, s2 = self.soc_limit # s1 soc的下限,s2 soc的上限
def Stor_soc_constr_rule1(model,timepoint):
return model.Stor_soc[timepoint] <= s2
model.Stor_soc_constr1 = pyo.Constraint(model.TimePoint, rule=Stor_soc_constr_rule1 )
def Stor_soc_constr_rule2(model,timepoint):
return model.Stor_soc[timepoint] >= s1
model.Stor_soc_constr2 = pyo.Constraint(model.TimePoint, rule=Stor_soc_constr_rule2 )
# SOC经过一个调控周期后=初始
model.Stor_soc_constr3 = pyo.Constraint(
expr=self.init_soc +sum(
[(model.Stor_In_M[timepoint]-model.Stor_Out_M[timepoint])*dt for timepoint in model.TimePoint]
)/ self.Upper== self.init_soc)
3、电源侧模型
def __init__(self, name: str,
Upper: float, # 最大买电功率
efficiency,
unit_cost: list, # 向公用电网购买电力时的单位成本
wt: list, # 风电功率
pt: list,# 光伏功率
):
新增了 电价与绿电出力的属性。
1)表达式
# 买电功率,热泵和电加热用电量减新能源发电量
def Grid_P(model,timepoint):
P = sum([model.Pump_P[timepoint,id] for id in model.pumpID]) + \
model.Stor_P[timepoint] + model.Stor_pump_P[timepoint] - \
(self.wt[timepoint] + self.pt[timepoint])
return P
model.Grid_P = pyo.Expression(model.TimePoint,rule = Grid_P)
# 买电成本
model.Grid_cost = pyo.Expression(
expr = sum([(model.Grid_P[timepoint] * self.unit_cost[timepoint] * dt) for timepoint in model.TimePoint]))
2)约束
# 买电功率约束,大于0,小于上限
def Grid_P_constr_rule1(model,timepoint):
return model.Grid_P[timepoint] >= 0
model.Grid_P_constr1 = pyo.Constraint(model.TimePoint, rule=Grid_P_constr_rule1)
def Grid_P_constr_rule2(model,timepoint):
return model.Grid_P[timepoint] <= self.Upper
model.Grid_P_constr2 = pyo.Constraint(model.TimePoint, rule=Grid_P_constr_rule2)
4、热力侧模型
不基于基类模型,设置如下属性
def __init__(self, name: str,
load: list, # 热负荷需求
FromT: float, # 供水温度
ToT: float, # 回水温度
):
1)表达式
热泵流量之和 - 存入储热罐的流量 + 储热罐流出的流量 = 供热流量
# 供热流量
def Heat_M_constr_rule(model,timepoint):
M_all = sum([model.Pump_M[timepoint,id] for id in model.pumpID]) - \
model.Stor_In_M[timepoint] + model.Stor_Out_M[timepoint]
return M_all
model.Heat_All_M = pyo.Expression(model.TimePoint, rule=Heat_M_constr_rule)
2)约束
- 储熱罐进水流量小于两个热泵的流量
def Stor_In_M_constr_rule(model,timepoint):
return model.Stor_In_M[timepoint]<=sum([model.Pump_M[timepoint,id] for id in model.pumpID])
model.Stor_In_M_constr = pyo.Constraint(model.TimePoint, rule=Stor_In_M_constr_rule)
- 热力平衡
供热流量 * 温差 * 比热 = 热力需求
def Heat_Q_constr_rule(model,timepoint):
return model.Heat_All_M[timepoint]*(self.FromT-self.ToT)*4.2*1000/3.6 == self.load[timepoint]
model.Heat_Q_constr = pyo.Constraint(model.TimePoint, rule=Heat_Q_constr_rule)
求解
扩充之前的 optimize 函数。指定 ipopt 作为求解器
def optimize(data,resources):
model = pyo.ConcreteModel()
model.TimePoint = pyo.Set(initialize=[i for i in range(len(data))]) # 采用列表初始化集合索引,表示时间点
for re in resources:
re.create_model(model, dt=15 / 60)
# 设定最小化优化目标
model.allcost = pyo.Objective(rule=model.Grid_cost, sense=pyo.minimize)
# 求解
opt = pyo.SolverFactory('ipopt') # 指定 ipopt 作为求解器
solution = opt.solve(model, symbolic_solver_labels=True) # 调用求解器求解
solution.write() # 写入求解结果
log_infeasible_constraints(model)
print(solution.solver.termination_condition) # 终止条件 一般包括三种 optimal, feasible, infeasible
print(solution.solver.termination_message) # 求解得到的信息 一般为一行字符串信息
print(solution.solver.status) # 表示求解的状态 包括 ok, warning, error, aborted, or unknown
return model
优化结果分析
1、情景 1
没有绿电,所有电力均来自电网。电价为阶梯式电价,其中时间点 40 到 80 电价较高。分别计算最优方案的热泵流量、储热罐流量、购买电力、全天电费。
Solver:
- Status: ok
Message: Ipopt 3.12.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 1.3437001705169678
# ----------------------------------------------------------
optimal objective: 3727.5781256704713
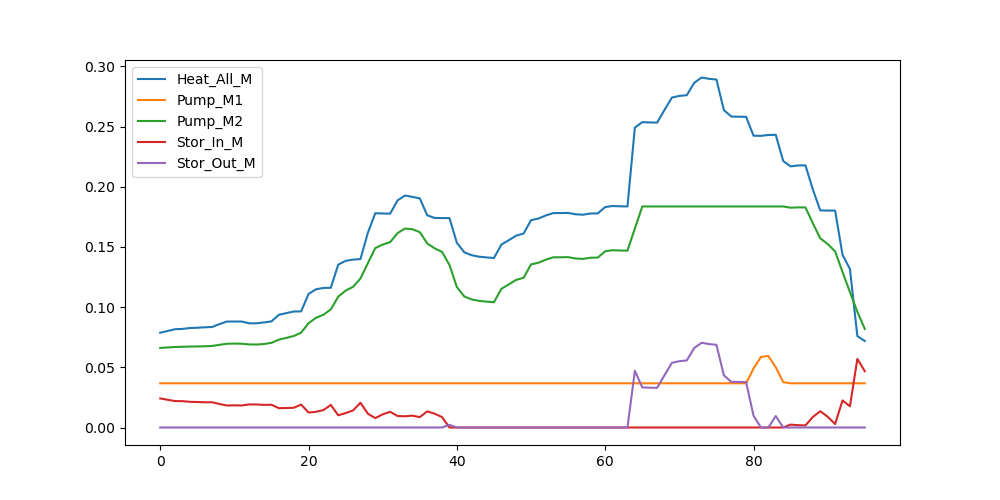
分析:
全天总供电费用:3727.5 元
因为可以根据电价与负荷的情况选择热力来源与是否蓄能所以:
- 1 号热泵 cop 较低,所以全程流量都较小,仅在时刻 80 附近由于储热罐容量不足时增加了流量。
- 2 号热泵曲线与负荷基本一致,在时刻 65 到 85 附近负荷达到上限。
- 储热罐在电价较低且负荷较低的的时段存入部分热水,在 65 至 85 负荷较大且电价较高的时段放出热水。
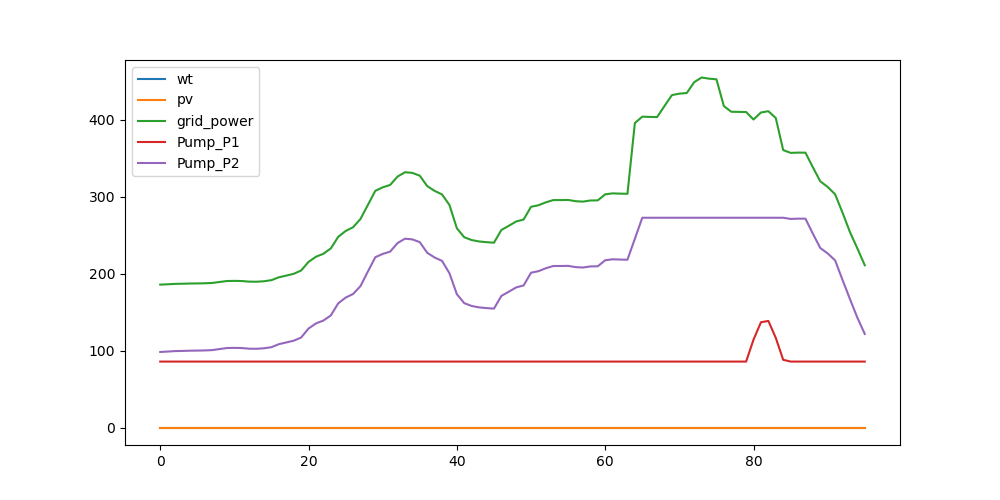
电力数据与流量数据体现的内容一致。
2、情景 2
增加绿电,不足的电力向电网购买。电价为阶梯式电价,其中时间点 40 到 80 电价较高。分别计算最优方案的热泵流量、储热罐流量、购买电力、全天电费。
Solver:
- Status: ok
Message: Ipopt 3.12.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 1.3954508304595947
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
optimal objective: 2313.878033993671
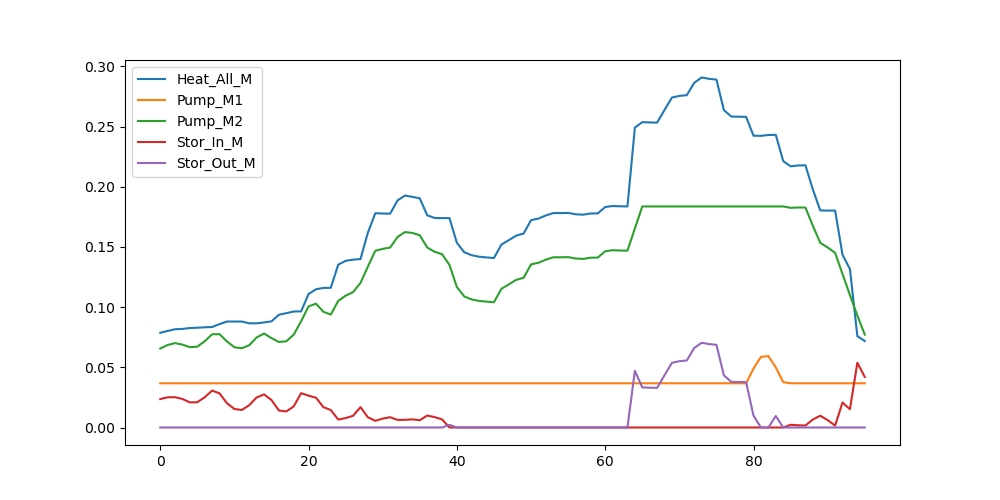
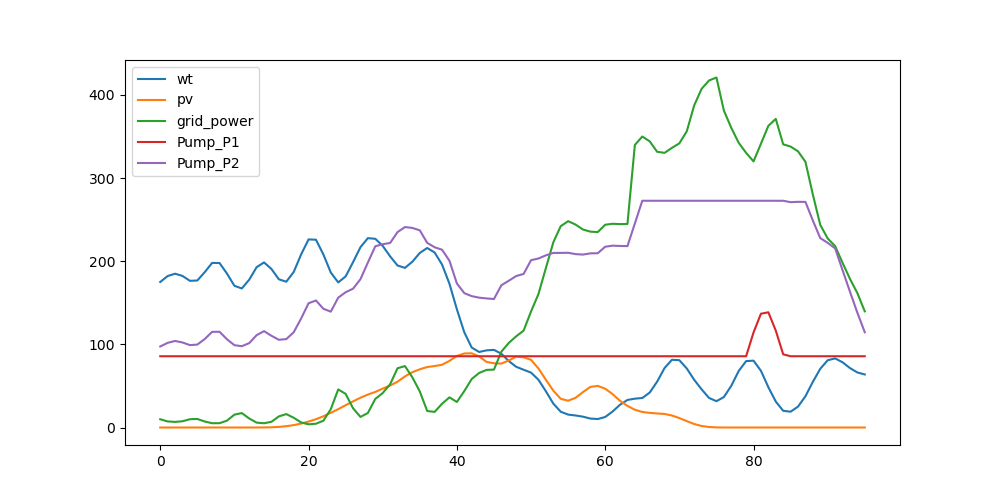
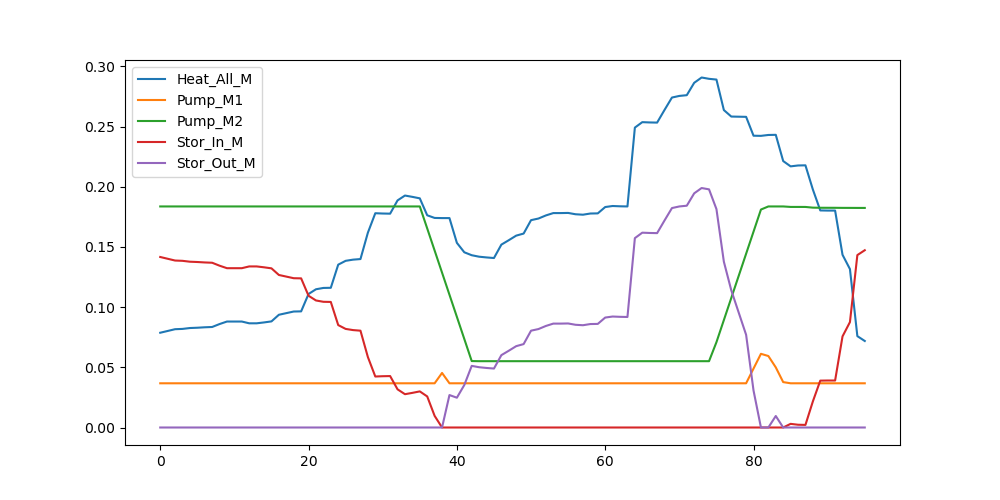
分析:
全天总供电费用:2313.8元
因为有了绿电做补充所以很明显的费用下降:
- 热泵的曲线与情景 1 基本一致,仅在 0 到 40 的时段内由于风电的波动导致了 2 号热泵负荷的波动。
- 购买的电力由于绿电的提供,前半天曲线明显降低。
3、情景 3
在情景 2 的基础上,调整储热损失为 0.5 度。分别计算最优方案的热泵流量、储热罐流量、购买电力、全天电费。
Solver:
- Status: ok
Message: Ipopt 3.12.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.9821372032165527
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
optimal objective: 2003.602815292267
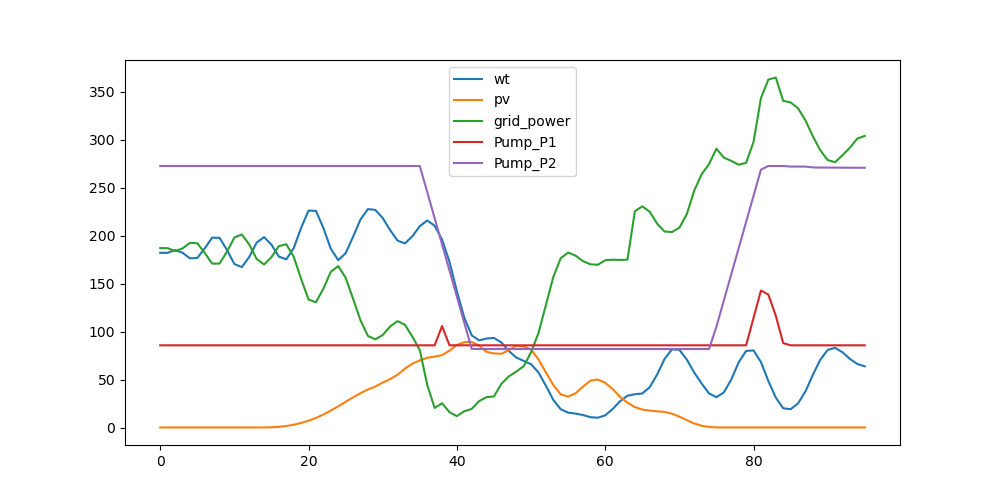
分析:
全天总供电费用:2003.6元
- 由于降低了储能损失,在电价较低且有绿电的情况下,储能量相比情景 2 大幅增加,从而也降低了成本。
- 2 号热泵在电价较低且有绿电的情况下满负荷运行,在高电价时段为最低负荷运行。
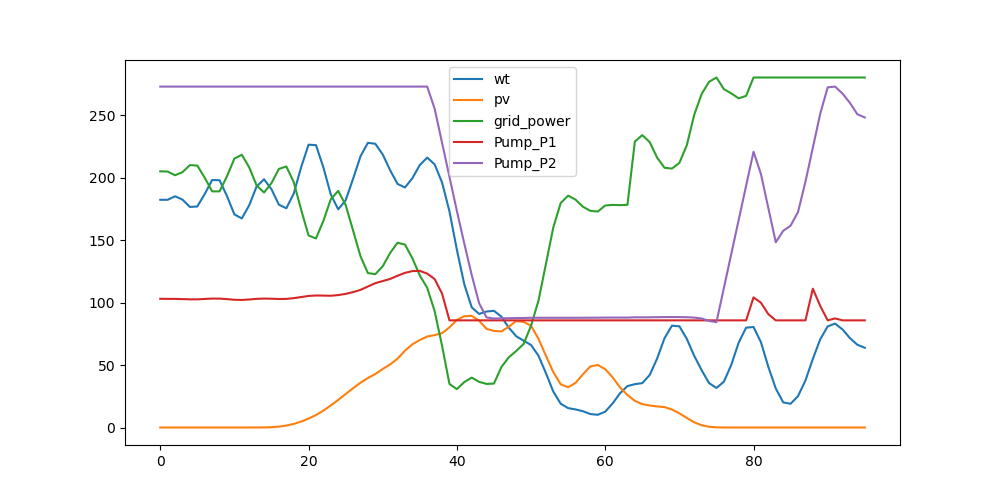
4、情景 4
在情景 3 的基础上,限制购电功率为 280。分别计算最优方案的热泵流量、储热罐流量、购买电力、全天电费。
Solver:
- Status: ok
Message: Ipopt 3.12.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.9911162853240967
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
optimal objective: 2057.101508010534
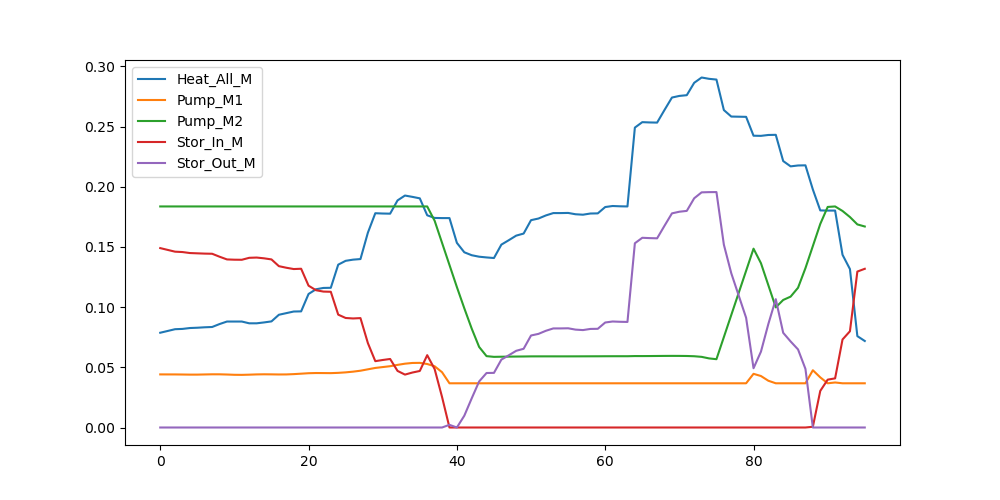
分析:
全天总供电费用:2057.1 元
限制购电功率的情况下,为满足负荷需求从而会增加储能量,但储能存在损失也会耗能所以成本反而增加。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号