算法练习 01-最大连续子序列和

循环遍历

时间复杂度：O(n^2）

int maxSubSum(const vector<int>& v) {
	int ans = 0;
	for (int i = 0; i < (int)v.size(); i++) {
		int thisans = 0;
		for (int j = i; j < (int)v.size(); j++) {
			thisans += v[j];
			if (thisans > ans) {
				ans = thisans;
			}
		}
	}
	return ans;
}

分治算法Divide-and-conquer

以序列中间项为界，最优子序列只会出现三种情况，即子序列在中间项的左侧，在中间项的右侧或者包含中间项。将问题分解为左右两边，得到左右两边的结果后再进行合并。

时间复杂度：O(NlogN)

int maxSubSum(const vector<int>& v, int l, int r) {
	if (l == r) {
		return v[l];
	}

	int m = (l + r) / 2;
	int maxLeftSum = maxSubSum(v, l, m);
	int maxRightSum = maxSubSum(v, m + 1, r);

	int maxMidLeft = 0, MidLeft = 0;	//由于此处限制无法处理最大子序列和小于0的情况
	for (int i = m; i >= l; --i) {
		MidLeft += v[i];
		if (MidLeft > maxMidLeft) {
			maxMidLeft = MidLeft;
		}
	}
	int maxMidRight = 0, MidRight = 0;
	for (int i = m + 1; i <= r; ++i) {
		MidRight += v[i];
		if (MidRight > maxMidRight) {
			maxMidRight = MidRight;
		}
	}

	return max(maxLeftSum, max(maxRightSum, maxMidLeft + maxMidRight));
}

分析简化（联机算法On-line algorithm）

任何负的子序列不可能是最优子序列的前缀。

时间复杂度：O(n)

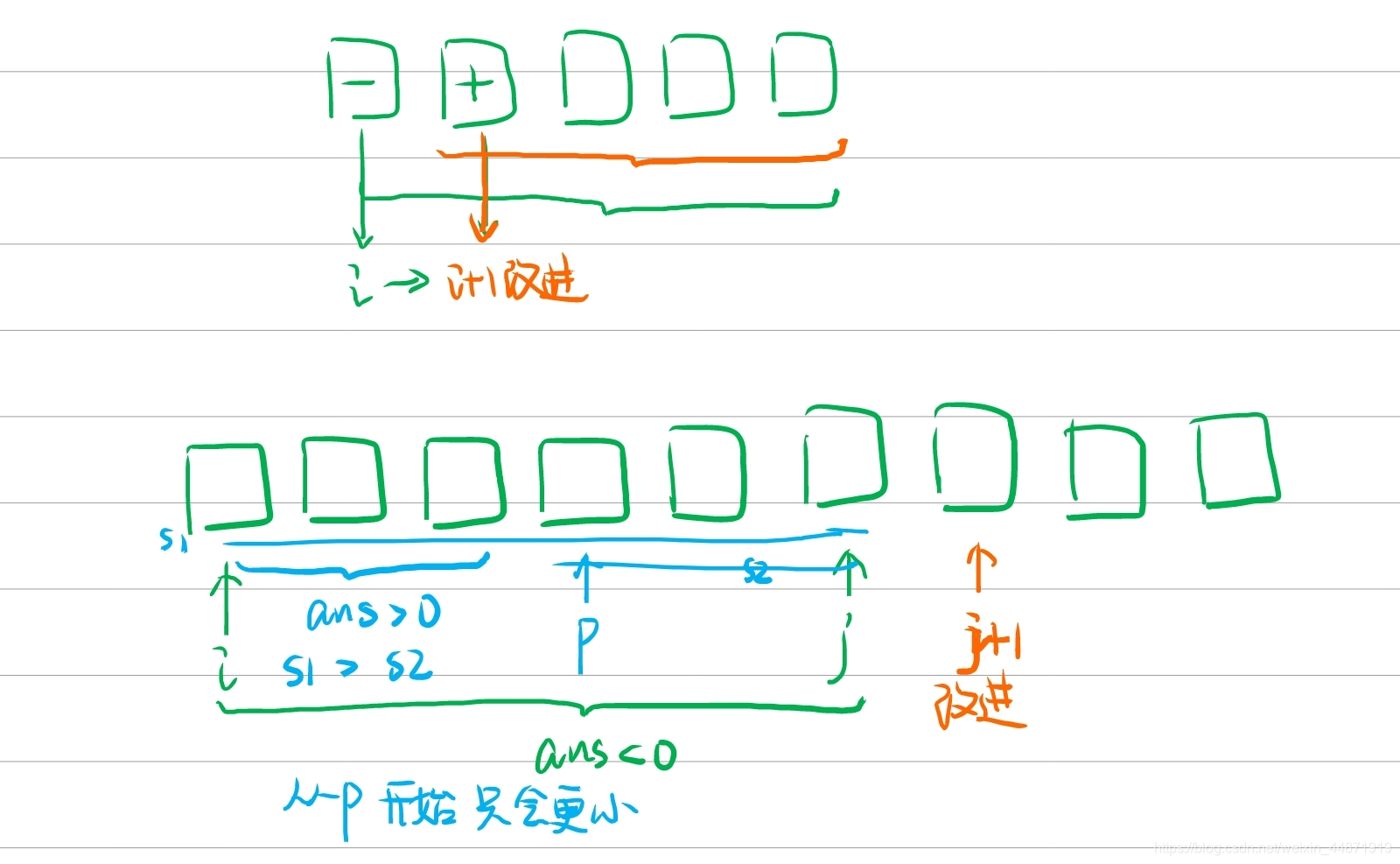
int maxSubSum(const vector<int>& v) {
	int ans = 0, thisans = 0;
	for (auto &x : v) {
		thisans += x;
		if (thisans > ans) {
			ans = thisans;
		}
		else if(thisans < 0) {
			thisans = 0;
		}
	}
	return ans;
}

参考资料

Data Structure and Algorithm Analysis in C++(Fourth Edition), Mark Allen Weiss