阿里网盘pdf文件分享
1 进入数学快速入门官网文档
![image-20210818092328825]()
进入到
![image-20210818092355321]()
拉到网页最下面
![image-20210818092440359]()
点击面向数学学习的快速入门指南即可进入官方数学学习教程
2 面向数学学习的快速入门指南
2.1 内容输入
在网络或桌面 Wolfram 笔记本中,只须输入内容,然后按下 SHIFT+ENTER 进行计算:
| In[1]:= |
![img]() |
| Out[1]= |
![img]() |
In[n] 和 Out[n] 标示出相邻的输入和输出. % 符号指代最近的输出:
| In[1]:= |
![Click for copyable input]() |
| Out[1]= |
![img]() |
| In[2]:= |
![Click for copyable input]() |
| Out[2]= |
![img]() |
执行完计算以后,建议栏会提供下一步计算的建议:
![img]()
在数学运算中可以使用标准符号:
(用空格或 * 表示乘法,不要用字符 “x”.)
| In[1]:= |
![Click for copyable input]() |
| Out[1]= |
![img]() |
用小括号(不是中括号或大括号)显示不同层次的组合:
| In[2]:= |
![Click for copyable input]() |
| Out[2]= |
![img]() |
Wolfram 语言有大约 6,000 个内置函数,涵盖了各个方面的数学知识.
用逗号分隔内置函数的参数,并将其置于方括号内:
| In[1]:= |
![Click for copyable input]() GCD[12, 15] |
| Out[1]= |
![img]() |
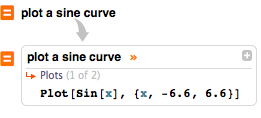
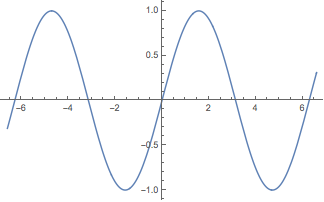
如果不知道使用哪个函数,在行的开始处键入 = 即可进行自然语言输入:
| In[2]:= |
![img]() plot a sine curve |
|
|
| Out[2]= |
![img]() |
|
|
Lists 表示一些项的集合,用 { ... } 表示:
| In[1]:= |
![Click for copyable input]() {1, 2, 3} {x, y, z} |
列表是有序的. 可以包含数字、变量、计算,甚至是其他列表:
许多运算是被应用到每个元素上的:
| In[2]:= |
![Click for copyable input]() {1, 2, 3} + 2 |
| Out[2]= |
![img]() |
从 1 开始,可以用 [[ ... ]] 来提取列表的元素:
| In[3]:= |
![Click for copyable input]() {a, b, c, d}[[3]] |
| Out[3]= |
![img]() |
通过使用如 Range 这样的函数可以轻松构建列表:
| In[1]:= |
![Click for copyable input]() Range[10] |
| Out[1]= |
![img]() |
2.2 分数与小数
在 Wolfram 语言中,精确输入(如分数)会提供精确的输出:
(用 CTRL+ / 输入分数.)
| In[1]:= |
![Click for copyable input]() 1/4 + 1/3 |
| Out[1]= |
![img]() |
用 Together 写成最小公分母的形式:
| In[2]:= |
![Click for copyable input]() Together[1/a + 1/b] |
| Out[2]= |
![img]() |
任何含有小数的输入给出近似输出:
| In[1]:= |
![Click for copyable input]() .25 + 1/3 |
| Out[1]= |
![img]() |
用 N 得到结果的数字近似值:
| In[2]:= |
![Click for copyable input]() N[1/4 + 1/7] |
| Out[2]= |
![img]() |
指定所示答案的准确度:
| In[3]:= |
![Click for copyable input]() N[1/4 + 1/7, 10] |
| Out[3]= |
![img]() |
有些数字表示成 ScientificForm 形式会更合适:
| In[1]:= |
![Click for copyable input]() ScientificForm[0.00123] |
| Out[1]= |
![img]() |
在适合的情况下,系统自动使用 ScientificForm 形式:
| In[2]:= |
![Click for copyable input]() N[100!] |
| Out[2]= |
![img]() |
2.3 变量与函数
变量以字母开头,可以含有数字:
(最好是用小写字母,把大写开头留给内置函数.)
| In[1]:= |
![Click for copyable input]() a1/2 |
| Out[1]= |
![img]() |
两个变量或数字间的空格表示相乘:
(换句话说,“a b” 表示 a 乘以 b,而 “ab” 则为变量 ab.)
| In[2]:= |
![Click for copyable input]() a b + 5 x x |
| Out[2]= |
![img]() |
用 /. 和 -> 在表达式中进行替代操作:
(可用 -> 输入 “rule” -> .)
| In[3]:= |
![Click for copyable input]() 1 + 2 x /. x -> 2 |
| Out[3]= |
![img]() |
用 = 符号赋值:
| In[1]:= |
![Click for copyable input]() x = 2 |
| Out[1]= |
![img]() |
在表达式和命令中使用变量:
| In[2]:= |
![Click for copyable input]() 1 + 2 x |
| Out[2]= |
![img]() |
清除赋值,x 保持未计算状态:
| In[3]:= |
![Click for copyable input]() Clear[x] 1 + 2 x |
| Out[3]= |
![img]() |
用 f[x_]:= 来定义自己的函数:
| In[1]:= |
![Click for copyable input]() f[x_] := 1 + 2 x |
x_ 表示 x 是一个模式,任何值都可以取代它.
:= 表示在计算时传递给 f 的任何参数将被代入右侧:
| In[2]:= |
![Click for copyable input]() f[2] |
| Out[2]= |
![img]() |
2.4 代数
可以因式分解或展开代数表达式:
(用 CTRL+6 输入排版式指数.)
| In[1]:= |
![Click for copyable input]() Factor[x^2 + 2 x + 1] |
| Out[1]= |
![img]() |
Wolfram 语言用 == (两个等号)检测是否相等:
| In[1]:= |
![Click for copyable input]() 2 + 2 == 4 |
| Out[1]= |
![img]() |
用 == 把代数表达式组合在一起表示方程:
| In[2]:= |
![Click for copyable input]() 1 + z == 15 |
| Out[2]= |
![img]() |
像 Solve 这样的命令给出的是方程的精确解:
| In[1]:= |
![Click for copyable input]() Solve[x^2 + 5 x - 6 == 0, x] |
| Out[1]= |
![img]() |
如果想要得到近似结果,用 NSolve:
| In[2]:= |
![Click for copyable input]() NSolve[7 x^2 + 3 x - 5 == 0, x] |
| Out[2]= |
![img]() |
以列表形式把一个方程组传递给函数:
| In[3]:= |
![Click for copyable input]() Solve[{x^2 + 5 == y, 7 x - 5 == y}, {x, y}] |
| Out[3]= |
![img]() |
求方程的根:
(|| 是 Or 的符号.)
| In[1]:= |
![Click for copyable input]() Roots[x^2 + 3 x - 4 == 0, x] |
| Out[1]= |
![img]() |
如果一个多项式不易被因式分解,近似结果可能更有用:
| In[2]:= |
![Click for copyable input]()
NRoots[360 + 234 x - 1051 x^2 + 11 x^3 + 304 x^4 - 20 x^5 == 0, x] |
| Out[2]= |
![img]() |
Reduce 命令可把一组不等式化简成简单的形式:
(可键入 <= 得到 ≤ 符号.)
| In[1]:= |
![Click for copyable input]() Reduce[{0 < x < 2, 1 <= x <= 4}, x] |
| Out[1]= |
![img]() |
简化形式可以包含多个区间:
| In[2]:= |
![Click for copyable input]() Reduce[(x - 1) (x - 2) (x - 3) (x - 4) > 0, x] |
| Out[2]= |
![img]() |
NumberLinePlot 是可视化这些结果的简便方法:
| In[3]:= | ![Click for copyable input]()
NumberLinePlot[x < 1 || 2 < x < 3 || x > 4, {x, -10, 10}] |
| ------- | ------------------------------------------------------------ |
| Out[3]= |
![img]() |
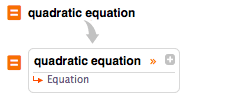
通过自然语言输入可以得到许多方程和公式:
| In[1]:= |
![img]() quadratic equation |
| Out[1]= |
![img]() |
2.5 二维绘图
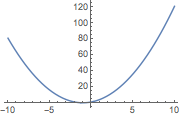
生成多项式函数的二维曲线:
(区间 {x,min,max} 定义了绘图范围.)
| In[1]:= |
![Click for copyable input]() Plot[x^2 + 2 x + 1, {x, -10, 10}] |
| Out[1]= |
![img]() |
或者绘制一组不等式的二维区域:
(&& 是 And 的符号.)
| In[2]:= |
![Click for copyable input]() RegionPlot[Reduce[{x^2 + y < 2 && x + y < 1}], {x, -3, 3}, {y, -3, 3}] |
| Out[2]= |
![img]() |
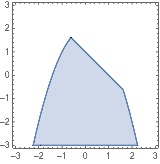
有许多有用的选项可以用来自定义可视化,比如,可以加上图例:
| In[1]:= |
![Click for copyable input]() Plot[{x^3, x^2, x}, {x, -2, 2}, PlotLegends -> "Expressions"] |
| Out[1]= |
![img]() |
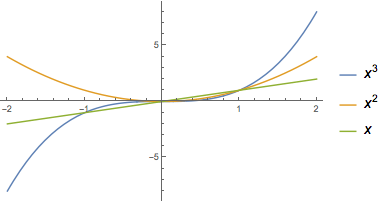
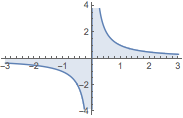
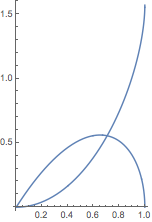
或对绘图进行填充来查看曲线下的面积:
| In[2]:= |
![Click for copyable input]() Plot[1/x, {x, -3, 3}, Filling -> Axis] |
| Out[2]= |
![img]() |
用 Show 来组合不同的绘图类型:
| In[1]:= |
![Click for copyable input]() Show[{Plot[x^2 + 2, {x, -3, 3}], RegionPlot[2 x > y - 3, {x, -3, 3}, {y, 0, 9}]}] |
| Out[1]= |
![img]() |
2.6 几何
Graphics 命令可以生成各种各样的二维形状:
| In[1]:= |
![Click for copyable input]() Graphics[Disk[]] |
| Out[1]= |
![img]() |
许多几何对象接受一系列坐标(列表)作为参数:
| In[2]:= |
![Click for copyable input]() Graphics[Rectangle[{0, 0}, {4, 2}]] |
| Out[2]= |
![img]() |
与指令一起以列表形式传递参数,把图形组合在一起并改变它们的样式:
| In[3]:= |
![Click for copyable input]() Graphics[{Green, Rectangle[{0, 0}, {2, 2}], Red, Disk[]}] |
| Out[3]= |
![img]() |
用诸如 SASTriangle 这样的命令生成三角形:
(键入 ESC+deg+ESC 可输入 ° 符号.)
| In[1]:= |
![Click for copyable input]() tr = SASTriangle[1, 90 \[Degree], 2] |
| Out[1]= |
![img]() |
可以直接算出如面积这样的属性:
| In[2]:= |
![Click for copyable input]() Area[tr] |
| Out[2]= |
![img]() |
把该表达式传递给 Graphics:
| In[3]:= |
![Click for copyable input]() Graphics[tr] |
| Out[3]= |
![img]() |
同样,可以用 Graphics3D 显示三维物体:
| In[1]:= |
![Click for copyable input]() Graphics3D[Ball[]] |
| Out[1]= |
![img]() |
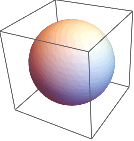
计算体积及其他属性:
(如果没有给出参数,圆柱的半径为1,高度为 2.)
| In[2]:= |
![Click for copyable input]() Volume[Cylinder[]] |
| Out[2]= |
![img]() |
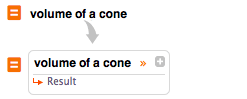
还可以用自然语言输入查找公式和其他信息:
| In[3]:= |
![img]() volume of a cone |
| Out[3]= |
![img]() |
系统还内置有几何变换,如 Rotate、Translate 和 Scale:
| In[1]:= |
![Click for copyable input]() Graphics[Rotate[Rectangle[], 45 \[Degree]]] |
| Out[1]= |
![img]() |
2.7 三角函数
对于基本的三角函数,可以使用标准的缩写形式(首字母大写):
| In[1]:= |
![Click for copyable input]() Sin[x]/Cos[x] == Tan[x] |
| Out[1]= |
![img]() |
加上 “Arc” 求反函数:
| In[2]:= |
![Click for copyable input]() ArcTan[1] |
| Out[2]= |
![img]() |
在弧度表达式中使用 Pi:
(键入 ESC+pi+ESC 来输入 π 字符.)
| In[1]:= |
![Click for copyable input]() Sin[\[Pi]/2] |
| Out[1]= |
![img]() |
或输入 ESCd+eg+ESC 得到内置的 Degree 符号:
| In[2]:= |
![Click for copyable input]() Sin[90 \[Degree]] |
| Out[2]= |
![img]() |
用恒等式自动展开(或化简)三角表达式:
| In[1]:= |
![Click for copyable input]() TrigExpand[Sin[2 x]] |
| Out[1]= |
![img]() |
因式分解三角多项式:
| In[2]:= |
![Click for copyable input]() TrigFactor[Cos[x]^2 - Sin[x]^2] |
| Out[2]= |
![img]() |
也可以使用像 Solve 这样的函数:
| In[1]:= |
![Click for copyable input]() Solve[Cos[x]^2 + Sin[x]^2 == x] |
| Out[1]= |
![img]() |
指定解的值域:
| In[2]:= |
![Click for copyable input]() Solve[{Tan[x] == 1, 0 < x < 2 Pi}] |
| Out[2]= |
![img]() |
2.8 极坐标
创建二维极坐标图:
(键入 ESC+th+ESC 可得到 θ 符号.)
| In[1]:= |
![Click for copyable input]() PolarPlot[Sin[2 \[Theta]] + Cos[2 \[Theta]], {\[Theta], 0, 2 Pi}] |
| Out[1]= |
![img]() |
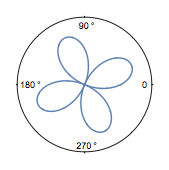
显示极坐标轴:
| In[2]:= |
![Click for copyable input]() PolarPlot[Sin[2 \[Theta]] + Cos[2 \[Theta]], {\[Theta], 0, 2 Pi}, PolarAxes -> Automatic, PolarTicks -> {0 \[Degree], 90 \[Degree], 180 \[Degree], 270 \[Degree]}] |
| Out[2]= |
![img]() |
把直角坐标转换成极坐标:
| In[1]:= |
![Click for copyable input]() ToPolarCoordinates[{1, 1}] |
| Out[1]= |
![img]() |
2.9 指数和对数
Wolfram 语言用 E 表示指数常数.
Log 给出一个表达式的自然对数:
| In[1]:= |
![Click for copyable input]() Log[E^2] |
| Out[1]= |
![img]() |
计算以 2 为基数的对数:
| In[2]:= |
![Click for copyable input]() Log[2, 64] |
| Out[2]= |
![img]() |
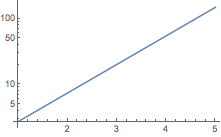
在对数刻度上绘图:
| In[1]:= |
![Click for copyable input]() LogPlot[E^x, {x, 1, 5}] |
| Out[1]= |
![img]() |
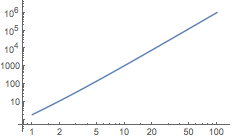
把两个坐标轴都设成对数刻度:
| In[2]:= |
![Click for copyable input]() LogLogPlot[x^2 + x^3, {x, 1, 100}] |
| Out[2]= |
![img]() |
2.10 极限
计算表达式的极限值:
(键入 -> 可得到 符号.)
| In[1]:= |
![Click for copyable input]() Limit[(x^3 - 1)/(x - 1), x -> 1] |
| Out[1]= |
![img]() |
求 Infinity 处的极限:
(键入 ESC+inf+ESC 可得到 ∞ 符号.)
| In[2]:= |
![Click for copyable input]() Limit[(2 x^3 - 1)/(5 x^3 + x - 1), x -> \[Infinity]] |
| Out[2]= |
![img]() |
还可以指定极限的方向.
设置为 1 时从左侧逼近极限:
| In[1]:= |
![Click for copyable input]() Limit[1/x, x -> 0, Direction -> 1] |
| Out[1]= |
![img]() |
设置为 -1 时从右侧逼近极限:
| In[2]:= |
![Click for copyable input]() Limit[1/x, x -> 0, Direction -> -1] |
| Out[2]= |
![img]() |
用 HoldForm 将表达式保持为未计算状态:
(TraditionalForm 用传统的数学排版形式显示.)
| In[1]:= |
![Click for copyable input]() TraditionalForm[HoldForm[Limit[1/x, x -> Infinity]]] |
| Out[1]= |
![img]() |
2.11 导数
用命令 D 计算导数:
| In[1]:= |
![Click for copyable input]() D[x^6, x] |
| Out[1]= |
![img]() |
或者使用角分符号:
| In[2]:= |
![Click for copyable input]() Sin'[x] |
| Out[2]= |
![img]() |
对用户定义的函数求导:
| In[1]:= |
![Click for copyable input]()
f[x_] := x^2 + 2 x + 1; f'[x] |
| Out[1]= |
![img]() |
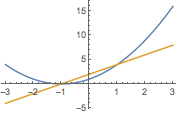
绘制导数:
| In[2]:= |
![Click for copyable input]() Plot[{f[x], f'[x]}, {x, -3, 3}] |
| Out[2]= |
![img]() |
还可以多次求导:
| In[1]:= |
![Click for copyable input]() D[x^6, {x, 3}] |
| Out[1]= |
![img]() |
或者多次使用 ' 符号:
| In[2]:= |
![Click for copyable input]() Sin''[x] |
| Out[2]= |
![img]() |
和前面讨论过的主题一样,也可以通过自然语言输入得到微积分公式:
| In[1]:= |
![img]() product rule formula |
| Out[1]= |
![img]() |
2.12 积分
用 Integrate 计算积分:
| In[1]:= |
![Click for copyable input]() Integrate[8 x^4, x] |
| Out[1]= |
![img]() |
或输入 ESC+intt+ESC 得到一个可填充的数学表达式:
(如果想了解更多关于可填充表达式的信息,请参阅数学排版显示.)
| In[2]:= |
![Click for copyable input]() \[Integral]8 x^4 \[DifferentialD]x |
| Out[2]= |
![img]() |
对于定积分,输入 ESC+dintt+ESC 并指定上下限:
| In[1]:= |
![Click for copyable input]() \!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Pi]\)]\(Sin[ x] \[DifferentialD]x\)\) |
| Out[1]= |
![img]() |
用 NIntegrate 来得到数值近似:
| In[2]:= |
![Click for copyable input]()
NIntegrate[x^3 Sin[x] + 2 Log[3 x]^2, {x, 0, Pi}] |
| Out[2]= |
![img]() |
2.13 序列、求和与级数
在 Wolfram 语言中,用列表表示整数序列.
用 Table 来定义一个简单的序列:
| In[1]:= |
![Click for copyable input]() Table[x^2, {x, 1, 7}] |
| Out[1]= |
![img]() |
系统内置有大家熟知的序列:
| In[2]:= |
![Click for copyable input]() Table[Fibonacci[x], {x, 1, 7}] |
| Out[2]= |
![img]() |
用 RecurrenceTable 定义递归序列:
(注意 {x,min,max} 表示法的使用.)
| In[1]:= |
![Click for copyable input]()
RecurrenceTable[{a[x] == 2 a[x - 1], a[1] == 1}, a, {x, 1, 8}] |
| Out[1]= |
![img]() |
计算序列的 Total:
| In[2]:= |
![Click for copyable input]() Total[%] |
| Out[2]= |
![img]() |
根据母函数计算序列的 Sum:
| In[1]:= |
![Click for copyable input]() Sum[i (i + 1), {i, 1, 10}] |
| Out[1]= |
![img]() |
用 ESC+sumt+ESC 得到可填充的排版形式:
| In[2]:= |
![Click for copyable input]()
\!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(10\)]\(i \((i + 1)\)\)\) |
| Out[2]= |
![img]() |
可以进行不定求和与多重求和计算:
| In[3]:= |
![Click for copyable input]()
\!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)]\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(n\)]i\ j\)\) |
| Out[3]= |
![img]() |
计算序列的母函数:
| In[1]:= |
![Click for copyable input]() FindSequenceFunction[{2, 4, 6, 8}, n] |
| Out[1]= |
![img]() |
生成几乎任意内置函数的组合的幂级数近似:
| In[1]:= |
![Click for copyable input]() Series[Exp[x^2], {x, 0, 8}] |
| Out[1]= |
![img]() |
O[x]9 表示省略掉的更高次数的项;用 Normal 来截断这些项:
| In[2]:= |
![Click for copyable input]() Normal[%] |
| Out[2]= |
![img]() |
给定一个未知或未定义的函数,Series 返回用导数表示的幂级数:
| In[3]:= |
![Click for copyable input]() Series[2 f[x] - 3, {x, 0, 3}] |
| Out[3]= |
![img]() |
系统可自动化简收敛级数:
| In[1]:= |
![Click for copyable input]() \!\( \*UnderoverscriptBox[\(\[Sum]\), \(n = 0\), \(\[Infinity]\)] \*SuperscriptBox[\(0.5\), \(n\)]\) |
| Out[1]= |
![img]() |
2.14 更多二维绘图
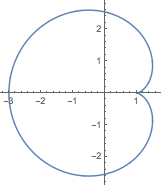
用 ParametricPlot 来绘制一组参数方程:
| In[1]:= |
![Click for copyable input]() ParametricPlot[{2 Cos[t] - Cos[2 t], 2 Sin[t] - Sin[2 t]}, {t, 0, 2 Pi}] |
| Out[1]= |
![img]() |
用多个变量绘制函数的 ContourPlot:
| In[1]:= |
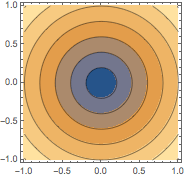
![Click for copyable input]() ContourPlot[Sqrt[x^2 + y^2], {x, -1, 1}, {y, -1, 1}] |
| Out[1]= |
![img]() |
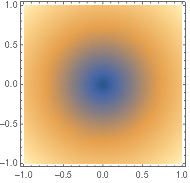
用 DensityPlot 绘制连续形式的图:
| In[2]:= |
![Click for copyable input]() DensityPlot[Sqrt[x^2 + y^2], {x, -1, 1}, {y, -1, 1}] |
| Out[2]= |
![img]() |
2.15 三维绘图
Plot3D 可绘制三维的笛卡尔曲线或曲面:
| In[1]:= |
![Click for copyable input]() Plot3D[x^2 - y^2 , {x, -3, 3}, {y, -3, 3}] |
| Out[1]= |
![img]() |
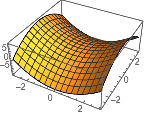
用 ParametricPlot3D 绘制三维空间曲线:
| In[2]:= |
![Click for copyable input]()
ParametricPlot3D[{Sin[u], Cos[u], u/10}, {u, 0, 20}] |
| Out[2]= |
![img]() |
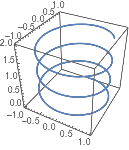
如果想在球面坐标系中绘图,用 SphericalPlot3D:
| In[3]:= |
![Click for copyable input]()
SphericalPlot3D[Sin[\[Theta]], {\[Theta], 0, Pi}, {\[Phi], 0, 2 Pi}] |
| Out[3]= |
![img]() |
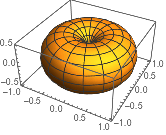
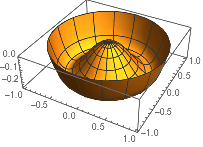
RevolutionPlot3D 通过绕轴旋转一个表达式构建曲面:
| In[1]:= |
![Click for copyable input]() RevolutionPlot3D[x^4 - x^2, {x, -1, 1}] |
| Out[1]= |
![img]() |
2.16 多变量微积分
D 可用于求偏导数,只需指定对哪个或哪些变量求导:
| In[1]:= |
![Click for copyable input]() D[x^3 z + 2 y^2 x + y z^3, y, z] |
| Out[1]= |
![img]() |
或使用 ∂ 符号:
(键入 ESC+pd+ESC 可以输入 ∂,CTRL+- 产生下标.)
| In[2]:= |
![Click for copyable input]()
\!\( \*SubscriptBox[\(\[PartialD]\), \(x, y\)]\(( \*SuperscriptBox[\(x\), \(2\)] - 2 x\ y + x\ y\ z)\)\) |
| Out[2]= |
![img]() |
多重积分与单个积分的符号是一样的:
(键入 ESC+int+ESC 可得到 ∫,用 ESC+dd+ESC 得到 ![image-20210818095739845]() .)
.)
| In[1]:= |
![Click for copyable input]()
\[Integral]\[Integral]\[Integral](x^2 + y^2 + z^2) \[DifferentialD]y \[DifferentialD]x \[DifferentialD]z |
| Out[1]= |
![img]() |
符号式结果常常相当复杂:
| In[2]:= |
![Click for copyable input]()
\!\( \*SubsuperscriptBox[\(\[Integral]\), \(-1\), \(1\)]\( \*SubsuperscriptBox[\(\[Integral]\), \(-2\), \(x\)]\((x\ Sin[ \*SuperscriptBox[\(y\), \(2\)]] + y\ Cos[ \*SuperscriptBox[\(x\), \(2\)]])\) \[DifferentialD]y \ \[DifferentialD]x\)\) |
| Out[2]= |
![img]() |
这种情况下,总可以通过使用 N 命令得到近似结果:
| In[3]:= |
![Click for copyable input]() N[%, 5] |
| Out[3]= |
![img]() |
2.17 矢量分析与可视化
在 Wolfram 语言中,用长度为 n 的列表表示 n 维矢量.
计算两个矢量的点积:
| In[1]:= |
![Click for copyable input]() {1, 2, 3}.{a, b, c} |
| Out[1]= |
![img]() |
输入 ESC+cross+ESC 得到叉乘符号:
| In[2]:= |
![Click for copyable input]() {1, 2, c}\[Cross]{a, b, c} |
| Out[2]= |
![img]() |
计算矢量的模:
| In[1]:= |
![Click for copyable input]() Norm[{1, 1, 1}] |
| Out[1]= |
![img]() |
求矢量在 x 轴上的投影:
| In[2]:= |
![Click for copyable input]() Projection[{8, 6, 7}, {1, 0, 0}] |
| Out[2]= |
![img]() |
求两个矢量的夹角:
| In[3]:= |
![Click for copyable input]() VectorAngle[{1, 0}, {0, 1}] |
| Out[3]= |
![img]() |
计算矢量的梯度:
(用 ESC+grad+ESC 输入 ∇ 符号.)
| In[1]:= |
![Click for copyable input]()
\!\( \*SubscriptBox[\(\[Del]\), \({x, y}\)]\({ \*SuperscriptBox[\(x\), \(2\)] + y, x + \*SuperscriptBox[\(y\), \(2\)]}\)\) |
| Out[1]= |
![img]() |
计算向量场的散度或旋度:
| In[2]:= |
![Click for copyable input]()
Div[{f[x, y, z], g[x, y, z], h[x, y, z]}, {x, y, z}] |
| Out[2]= |
![img]() |
Wolfram 语言拥有适合于可视化向量场的二维和三维函数:
| In[1]:= |
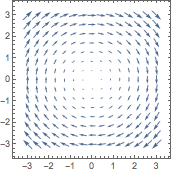
![Click for copyable input]() VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}] |
| Out[1]= |
![img]() |
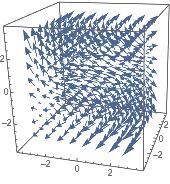
| In[2]:= |
![Click for copyable input]()
VectorPlot3D[{y, -x, z}, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}] |
| Out[2]= |
![img]() |
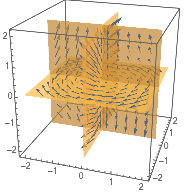
在切片曲面上绘制向量场:
| In[3]:= |
![Click for copyable input]()
SliceVectorPlot3D[{y, -x, z}, "CenterPlanes", {x, -2, 2}, {y, -2, 2}, {z, -2, 2}] |
| Out[3]= |
![img]() |
2.18 微分方程
Wolfram 语言可以求解常微分方程、偏微分方程和时滞微分方程 (ODE、PDE 和 DDE).
DSolveValue 接受微分方程并返回通解:
(C[1] 表示积分常数.)
| In[1]:= |
![Click for copyable input]() sol = DSolveValue[y'[x] + y[x] == x, y[x], x] |
| Out[1]= |
![img]() |
用 /. 替换常数:
| In[2]:= |
![Click for copyable input]() sol /. C[1] -> 1 |
| Out[2]= |
![img]() |
或为特解加上条件:
| In[3]:= |
![Click for copyable input]()
DSolveValue[{y'[x] + y[x] == x, y[0] == -1}, y[x], x] |
| Out[3]= |
![img]() |
NDSolveValue 可求出数值解:
| In[1]:= |
![Click for copyable input]()
NDSolveValue[{y'[x] == Cos[x^2], y[0] == 0}, y[x], {x, -5, 5}] |
| Out[1]= |
![img]() |
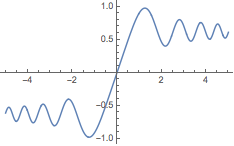
可直接绘制 InterpolatingFunction:
| In[2]:= |
![Click for copyable input]() Plot[%, {x, -5, 5}] |
| Out[2]= |
![img]() |
如果想要求解微分方程组,把所有方程和条件都放在列表中:
(注意:换行符没有任何影响.)
| In[1]:= |
![Click for copyable input]() {xsol, ysol} = NDSolveValue[ {x'[t] == -y[t] - x[t]^2, y'[t] == 2 x[t] - y[t]^3, x[0] == y[0] == 1}, {x, y}, {t, 20}] |
| Out[1]= |
![img]() |
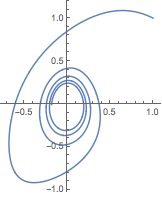
用参数图可视化解:
| In[2]:= |
![Click for copyable input]() ParametricPlot[{xsol[t], ysol[t]}, {t, 0, 20}] |
| Out[2]= |
![img]() |
2.19 复分析
虚部单位 ![img]() 表示为 I:
表示为 I:
| In[1]:= |
![Click for copyable input]() I^2 |
| Out[1]= |
![img]() |
许多运算可以自动处理复数:
| In[2]:= |
![Click for copyable input]() (1 + I) (2 - 3 I) |
| Out[2]= |
![img]() |
展开复数表达式:
| In[1]:= |
![Click for copyable input]() ComplexExpand[Sin[x + I y]] |
| Out[1]= |
![img]() |
在指数形式和三角函数形式之间转换表达式:
| In[2]:= |
![Click for copyable input]() ExpToTrig[E^(I x)] |
| Out[2]= |
![img]() |
| In[3]:= |
![Click for copyable input]() TrigToExp[%] |
| Out[3]= |
![img]() |
输入 ESC+co+ESC 可得到 Conjugate 符号:
| In[1]:= |
![Click for copyable input]() (3 + 2 I)\[Conjugate] |
| Out[1]= |
![img]() |
提取表达式的实部和虚部:
| In[2]:= |
![Click for copyable input]() ReIm[3 + 2 I] |
| Out[2]= |
![img]() |
或求绝对值和辐角:
| In[3]:= |
![Click for copyable input]() AbsArg[(1 + I)] |
| Out[3]= |
![img]() |
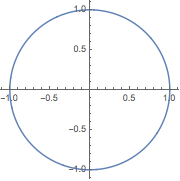
用 ParametricPlot 绘制保角映射:
| In[1]:= |
![Click for copyable input]()
ParametricPlot[ReIm[E^(I \[Omega])], {\[Omega], 0, 2 \[Pi]}] |
| Out[1]= |
![img]() |
在 PolarPlot 中使用 AbsArg:
| In[2]:= |
![Click for copyable input]()
PolarPlot[AbsArg[E^(I \[Omega])], {\[Omega], 0, \[Pi]}] |
| Out[2]= |
![img]() |
用 DensityPlot 可视化复分量:
| In[3]:= |
![Click for copyable input]()
DensityPlot[Im[ArcSin[(x + I y)^2]], {x, -2, 2}, {y, -2, 2}] |
| Out[3]= |
![img]() |
2.20 矩阵与线性代数
Wolfram 语言用列表的列表表示矩阵:
| In[1]:= |
![Click for copyable input]() {{1, 2}, {3, 4}} |
输入一个表格,用 CTRL+ ENTER 输入行,用 CTRL+ , 输入列:
| In[2]:= |
![Click for copyable input]() { {a, b}, {c, d} } |
| Out[2]= |
![img]() |
MatrixForm 将输出显示为一个矩阵:
| In[3]:= |
![Click for copyable input]() MatrixForm[{{a, b}, {c, d}}] |
| Out[3]= |
![img]() |
可以用迭代函数构建矩阵:
| In[1]:= |
![Click for copyable input]() Table[x + y, {x, 1, 3}, {y, 0, 2}] |
| Out[1]= |
![img]() |
或导入表示矩阵的数据:
| In[2]:= |
![Click for copyable input]() Import["data.csv"] |
| Out[2]= |
![img]() |
IdentityMatrix、DiagonalMatrix 和其他类似命令为内置符号.
标准的矩阵运算对元素进行操作:
| In[1]:= |
![Click for copyable input]() {1, 2, 3} {a, b, c} |
| Out[1]= |
![img]() |
计算两个矩阵的点积:
| In[2]:= |
![Click for copyable input]() {{1, 2}, {3, 4}}.{{a, b}, {c, d}} |
| Out[2]= |
![img]() |
求行列式:
| In[3]:= |
![Click for copyable input]() Det[{{a, b}, {c, d}}] |
| Out[3]= |
![img]() |
获取矩阵的逆:
| In[4]:= |
![Click for copyable input]() Inverse[{{1, 1}, {0, 1}}] |
| Out[4]= |
![img]() |
用 LinearSolve 求解线性系统:
| In[1]:= |
![Click for copyable input]() LinearSolve[{{1, 1}, {0, 1}}, {x, y}] |
| Out[1]= |
![img]() |
还有用于最小化和矩阵分解的函数.
2.21 离散数学
进行基本的数论运算,如因子分解:
| In[1]:= |
![Click for copyable input]() FactorInteger[30] |
| Out[1]= |
![img]() |
求任意两个整数的最大公约数(或最小公倍数 ):
| In[2]:= |
![Click for copyable input]() GCD[24, 60] |
| Out[2]= |
![img]() |
显示第 4 个质数:
| In[1]:= |
![Click for copyable input]() Prime[4] |
| Out[1]= |
![img]() |
判断一个数是否是质数:
| In[2]:= |
![Click for copyable input]() PrimeQ[%] |
| Out[2]= |
![img]() |
也可以进行互质判定:
| In[3]:= |
![Click for copyable input]() CoprimeQ[51, 15] |
| Out[3]= |
![img]() |
用 Mod 函数求余数:
| In[1]:= |
![Click for copyable input]() Mod[17, 5] |
| Out[1]= |
![img]() |
获取一个列表所有可能的排列:
| In[1]:= |
![Click for copyable input]() Permutations[{a, b, c}] |
| Out[1]= |
![img]() |
用不相交 Cycles 对列表应用 Permute:
(Cycles 接受列表的列表作为参数.)
| In[2]:= |
![Click for copyable input]()
Permute[{a, b, c, d}, Cycles[{{2, 4}, {1, 3}}]] |
| Out[2]= |
![img]() |
求置换阶数:
| In[3]:= |
![Click for copyable input]() PermutationOrder[Cycles[{{2, 4}, {1, 3}}]] |
| Out[3]= |
![img]() |
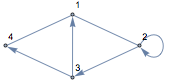
根据边的列表生成 Graph:
(用 ESC+ue+ESC 输入 UndirectedEdge,或用 ESC+de+ESC 输入 DirectedEdge.)
| In[1]:= |
![Click for copyable input]()
Graph[{1 <-> 2, 2 \[DirectedEdge] 3, 3 \[DirectedEdge] 4, 4 <-> 1, 3 \[DirectedEdge] 1, 2 \[DirectedEdge] 2}, VertexLabels -> All] |
| Out[1]= |
![img]() |
求两个顶点间最短的路径:
| In[2]:= |
![Click for copyable input]() FindShortestPath[%, 3, 2] |
| Out[2]= |
![img]() |
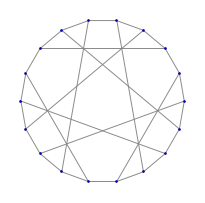
用自然语言输入了解众所周知的图:
| In[3]:= |
![img]() pappus graph image |
| Out[3]= |
![img]() |
2.22 概率
Wolfram 语言含有范围广泛的概率函数,以及几百个符号分布.
用数学符号计算阶乘:
| In[1]:= |
![Click for copyable input]() 5! |
| Out[1]= |
![img]() |
对于组合,可使用 Binomial:
| In[2]:= |
![Click for copyable input]() Binomial[4, 3] |
| Out[2]= |
![img]() |
计算二项分布的概率:
(键入 ESC+dist+ESC 可得到![image-20210818100548104]() 符号.)
符号.)
| In[1]:= |
![Click for copyable input]() Probability[x == 1, x \[Distributed] BinomialDistribution[1, 1/2]] |
| Out[1]= |
![img]() |
计算多项式的期望:
| In[2]:= |
![Click for copyable input]() Expectation[2 x + 3, x \[Distributed] NormalDistribution[]] |
| Out[2]= |
![img]() |
获取正态分布的符号式 PDF:
| In[1]:= |
![Click for copyable input]() PDF[NormalDistribution[0, 1], x] |
| Out[1]= |
![img]() |
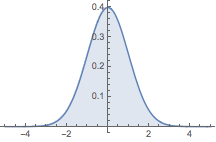
对结果绘图:
| In[2]:= |
![Click for copyable input]() Plot[%, {x, -5, 5}, Filling -> Axis] |
| Out[2]= |
![img]() |
自由格式输入可用来计算现实世界事件的概率:
| In[1]:= |
![img]() birthday problem 18 people |
| Out[1]= |
![img]() |
2.23 统计
在 Wolfram 语言中,统计函数可接受列表或符号分布作为参数:
计算一组数字的均值:
| In[1]:= |
![Click for copyable input]() Mean[{1, 2, 4, 5}] |
| Out[1]= |
![img]() |
求多个列表的相关:
| In[2]:= |
![Click for copyable input]() Correlation[{1, 3, 5}, {6, 4, 2}] |
| Out[2]= |
![img]() |
求泊松分布的标准差:
| In[3]:= |
![Click for copyable input]() StandardDeviation[PoissonDistribution[2]] |
| Out[3]= |
![img]() |
计算一组符号的矩:
| In[1]:= |
![Click for copyable input]() Moment[{x, y, z}, 2] |
| Out[1]= |
![img]() |
获取分布的矩母函数:
(键入 ESC+m+ESC 可得到 μ,或键入 ESC+s+ESC 得到 σ.)
| In[2]:= |
![Click for copyable input]() MomentGeneratingFunction[NormalDistribution[\[Mu], \[Sigma]], t] |
| Out[2]= |
![img]() |
用 RandomVariate 产生统计数据:
(用 //Short 来得到输出的简短总结.)
| In[1]:= |
![Click for copyable input]()
RandomVariate[NormalDistribution[0, 1], {500, 2}] // Short |
| Out[1]= |
![img]() |
可视化所得数据:
| In[2]:= |
![Click for copyable input]() Histogram3D[%] |
| Out[2]= |
![img]() |
2.24 绘制数据与最佳拟合曲线
用 ListPlot 绘制数据点:
| In[1]:= |
![Click for copyable input]() ListPlot[{1, 3, 4, 7, 9, 15}] |
| Out[1]= |
![img]() |
或用图表显示信息:
| In[2]:= |
![Click for copyable input]() BarChart[{1, 2, 3, 4, 5}] |
| Out[2]= |
![img]() |
有专门的函数绘制时间序列、金融数据,还有许多其他绘图函数.
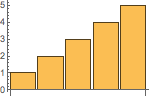
自动对多个数据集添加不同的颜色以示区分:
| In[1]:= |
![Click for copyable input]()
ListLinePlot[{{1, 2, 3, 4, 5}, {1, 3, 7, 10, 17}}] |
| Out[1]= |
![img]() |
|
|
通过使用如 PlotTheme 这样的选项可以改变绘图的样式和外观.
用 Fit 命令找到最佳拟合曲线:
({1,x,x2} 表示 x 的二次拟合.)
| In[1]:= |
![Click for copyable input]() Fit[{2, 3, 5, 7, 11, 13}, {1, x, x^2}, x] |
| Out[1]= |
![img]() |
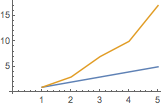
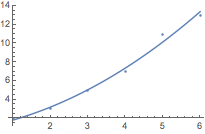
用 Show 将曲线与数据点相比较:
| In[2]:= |
![Click for copyable input]() Show[{Plot[%, {x, 1, 6}], ListPlot[{2, 3, 5, 7, 11, 13}]}] |
| Out[2]= |
![img]() |
2.25 群论
SymmetricGroup、AlternatingGroup、DihedralGroup 和许多其他已命名群属于内置符号.
获取群的元素列表:
| In[1]:= |
![Click for copyable input]() GroupElements[SymmetricGroup[2]] |
| Out[1]= |
![img]() |
确定群的生成元:
| In[2]:= |
![Click for copyable input]() GroupGenerators[SymmetricGroup[3]] |
| Out[2]= |
![img]() |
用两个生成元创建一个置换群:
| In[1]:= |
![Click for copyable input]()
PermutationGroup[{Cycles[{{3, 1, 2}}], Cycles[{{2, 5, 6}}]}] |
计算阶数:
| In[2]:= |
![Click for copyable input]() GroupOrder[%] |
| Out[2]= |
![img]() |
显示群的乘法表:
| In[1]:= |
![Click for copyable input]() TableForm[GroupMultiplicationTable[DihedralGroup[2]], TableHeadings -> Automatic] |
| Out[1]= |
![img]() |
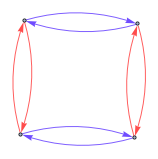
用 Cayley 图可视化:
| In[2]:= |
![Click for copyable input]() CayleyGraph[DihedralGroup[2]] |
| Out[2]= |
![img]() |
2.26 数学难题
Wolfram 语言是解决极具挑战性的数学难题和游戏的绝佳平台. 一旦明白其中的原理,用它来做研究就会得心应手.
假设你想在 100 万以内找出与 100 万没有公因子的正整数的个数.
那就从用 CoprimeQ 把前 100 万个正整数与 100 万相比开始.
| In[1]:= |
![Click for copyable input]() CoprimeQ[Range[1000000], 1000000] // Short |
| Out[1]= |
![img]() |
通过用 Nothing 替换结果为 False 的项,自动将其移除:
| In[2]:= |
![Click for copyable input]() % /. False -> Nothing // Short |
| Out[2]= |
![img]() |
然后计算所得列表的长度:
| In[3]:= |
![Click for copyable input]() Length[%] |
| Out[3]= |
![img]() |
把这些步骤放在一条命令中:
| In[4]:= |
![Click for copyable input]()
Length[CoprimeQ[Range[1000000], 1000000] /. False -> Nothing] |
| Out[4]= |
![img]() |
符号表达式经常能给出直接解. 给定一个正整数 k,你能找出计算 1k+2k+...+nk 的和的公式吗?
k=2 时的解:
| In[1]:= |
![Click for copyable input]()
\!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)] \*SuperscriptBox[\(i\), \(2\)]\) |
| Out[1]= |
![img]() |
通用解是第 n 个阶数为 −k 的调和数:
| In[2]:= |
![Click for copyable input]()
\!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)] \*SuperscriptBox[\(i\), \(k\)]\) |
|
|
| Out[2]= |
![img]() |
利用内置图形可以很容易地可视化几何问题. 来看下面的图形:
| In[1]:= |
![Click for copyable input]()
Labeled[Graphics[ shape = {Rectangle[], Rectangle[{0, 1}], Rectangle[{1, 0}]}], n] |
| Out[1]= |
![img]() |
对于给定的基底长度 n,可不可能用类似的基底长度为 1 的形状来填充这个图形?
n=2 时的解:
| In[2]:= |
![Click for copyable input]()
Graphics[{ Scale[shape, 2, {0, 0}], {Yellow, shape}, {Green, Translate[shape, {1, 1}]}, {Blue, Translate[Rotate[shape, -90 \[Degree]], {0, 2}]}, {Red, Translate[Rotate[shape, 90 \[Degree]], {2, 0}]} }] |
| Out[2]= |
![img]() |
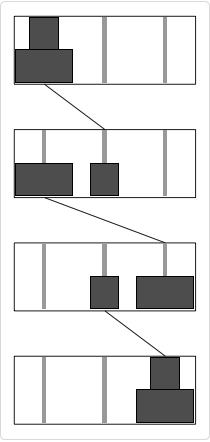
n=3 时的解:
| In[3]:= |
![Click for copyable input]()
Graphics[{ Scale[shape, 3, {0, 0}], {Orange, shape}, {Magenta, Translate[Rotate[shape, -90 \[Degree]], {0, 2}]}, {Green, Translate[shape, {1, 1}]}, {Red, Translate[Rotate[shape, 90 \[Degree]], {2, 0}]}, {Black, Translate[shape, {0, 4}]}, {Blue, Translate[Rotate[shape, 180 \[Degree]], {1, 4}]}, {Gray, Translate[shape, {2, 2}]}, {Purple, Translate[Rotate[shape, -90 \[Degree]], {4, 1}]}, {Yellow, Translate[Rotate[shape, 90 \[Degree]], {4, 0}]} }] |
| Out[3]= |
![img]() |
可以通过自然语言输入获取有名的游戏、难题和谜题:
| In[1]:= |
![img]() Tower of Hanoi 2 disk solution |
| Out[1]= |
![img]() |
2.27 交互模型
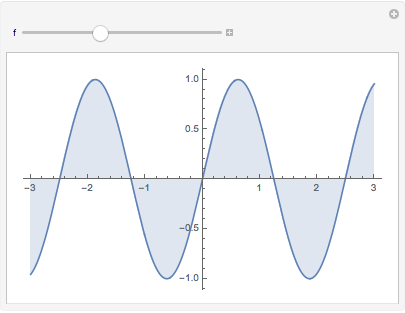
通过 Manipulate 命令可以交互式地实时查看改变参数会发生什么:
| In[1]:= |
![Click for copyable input]()
Manipulate[Plot[Sin[f x], {x, -3, 3}, Filling -> Axis], {f, 1, 5}] |
| Out[1]= |
![img]() |
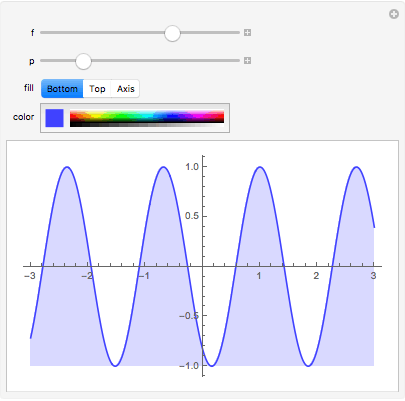
一个单独的 Manipulate 命令中可以有多个控件,Wolfram 语言将自动选择控件最合适的布局:
| In[1]:= |
![Click for copyable input]()
Manipulate[Plot[Sin[f*x + p], {x, -3, 3}, Filling -> fill, PlotStyle -> color], {f, 1, 5}, {p, 3, 9}, {fill, {Bottom, Top, Axis}}, {color, Red}] |
| Out[1]= |
![img]() |
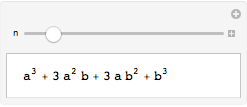
Wolfram 语言中的任意表达式都可被操控,包括非图形表达式:
| In[1]:= |
![Click for copyable input]() Manipulate[Expand[(a + b)^n], {n, 1, 20, 1}] |
| Out[1]= |
![img]() |
2.28 数学排版显示
用键盘快捷键(如 CTRL+/ 可用于分数的输入)插入可填充的排版表达式:
(点击方框突出显示并填充,或按下 TAB 在各方框间移动.)
![img]()
这是输入指数 (CTRL+6)、下标 (CTRL+-) 和其他常见表达式的简单方法.
在笔记本中按下 ESC 键得到 ![image-20210818102118972]() 符号,可用在键盘快捷输入形式
符号,可用在键盘快捷输入形式![image-20210818102206040]()
(在文档中常记为 ESC+alias+ESC )中.
键入正确的别名,当右侧的![image-20210818102118972]() 输入完成后,表达式就会发生改变:
输入完成后,表达式就会发生改变:
(偏微分 “partial derivative” 的别名是 “pd”.)
![img]()
产生求和、积分和其他高级表达式的方法为:
(定积分 “definite integral” 的别名是 “dintt”.)
![img]()
许多希腊字母和其他特殊字符也使用这种形式.
在桌面版的笔记本中,可以选择面板菜单中的“数学助手”查看可用的排版形式.
点击面板上的按钮即可在鼠标所在处插入一个可填充表达式:
![img]()
使用 TraditionalForm 命令以传统数学符号显示任意表达式:
| In[1]:= |
![Click for copyable input]() TraditionalForm[(y + 3)^2/((y - 2) (y + 5))] |
| Out[1]= |
![img]() |
用 SHIFT+CMD+T (SHIFT+ALT+T)把现有单元转换成 TraditionalForm:
(TraditionalForm 形式的表达式仍然是可计算的.)
| In[2]:= |
![Click for copyable input]() Limit[(x^2 - 1)/(x - 1), x -> 0] |
| In[3]:= |
![Click for copyable input]()
\!\(\*UnderscriptBox[\(lim\), \(x \[Rule] 0\)]\)( x^2 - 1)/(x - 1) |
| Out[3]= |
![img]() |
2.29 笔记本文档
可以在桌面或网页上使用 Wolfram 笔记本,它成功地把文字、图形、界面等与计算融合在一起:
![img]()
笔记本是按单元组织的,并由右边的方括号指定,
双击单元方括号打开或关闭单元组,
在单元间点击可以获取水平插入条,以便创建一个新的单元;
拷贝、粘贴、删除任何单元集合等.
选中任何单元集合并按住 SHIFT+ENTER 对输入进行计算.
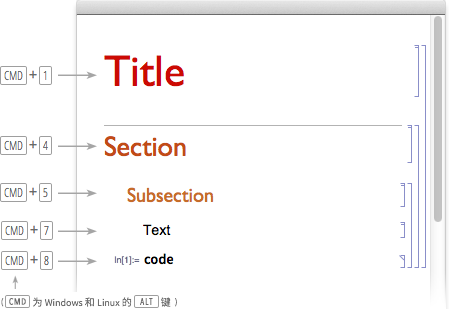
在笔记本中可以加上标题、章节或文本单元:
![img]()
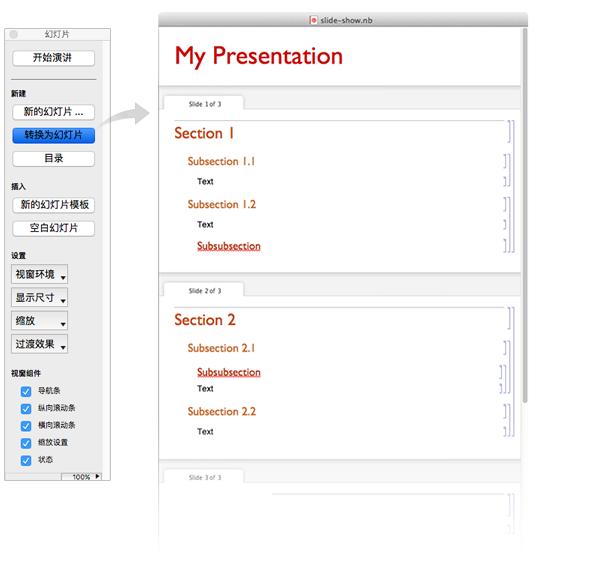
把笔记本转换成幻灯片也是易如反掌:
![img]()
与 Wolfram 语言的其他内容一样,文档也是可被程序化改变的符号表达式.
2.30 云部署
CloudDeploy 可把对象部署到 Wolfram Cloud.
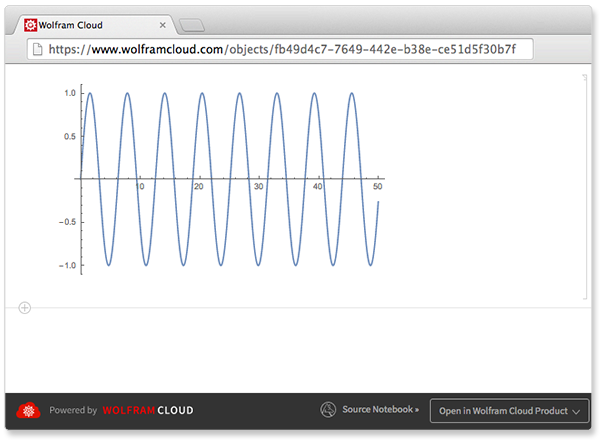
创建一个有正弦波图片的网页:
| In[1]:= |
![Click for copyable input]() CloudDeploy[Plot[Sin[x], {x, 0, 50}]] |
[Out1]=![img]()
![img]()
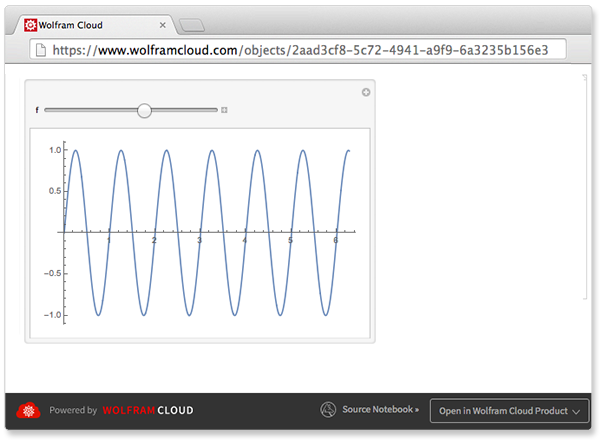
部署一个动态界面:
| In[1]:= |
![Click for copyable input]()
CloudDeploy[Manipulate[Plot[Sin[f x], {x, 0, 2 Pi}], {f, 1, 10}]] |
[Out1]=![img]()
![img]()
无论是否是动态部署,从笔记本部署的内容都会保留其样式.
用 CloudDeploy[Delayed[...]] 部署表达式,每次被请求时都对其重新进行计算.





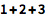
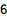
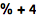
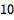

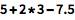
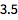
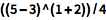
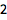
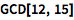
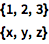
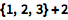
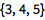
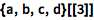
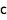
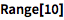

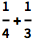
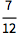
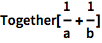
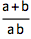
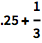
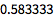
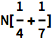
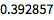
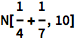
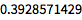

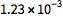
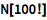
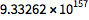
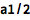
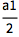
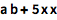
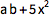
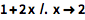
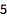
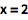
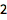
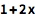
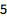

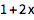
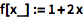
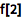
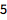
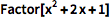
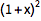
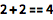
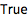
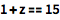
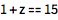
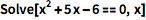
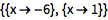
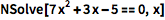
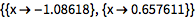
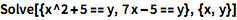
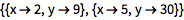
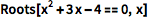
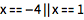

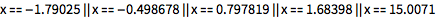
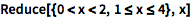
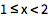
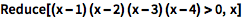
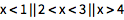
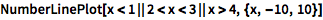


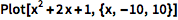
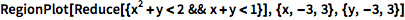

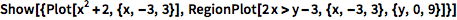

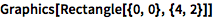



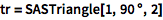
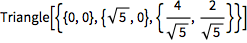
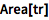
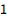


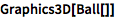
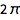

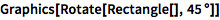

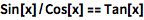
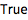
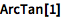
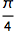
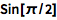
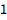
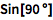
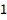
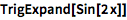
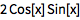
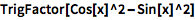
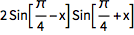
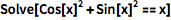
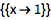
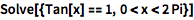
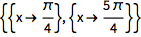
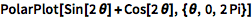
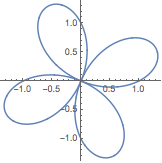
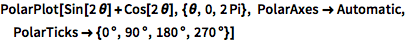
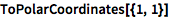
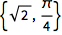
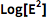
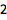
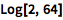
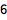
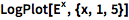
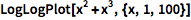
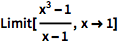
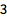
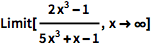
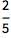
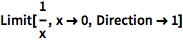
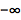
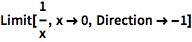
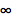
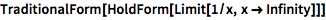
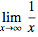
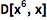
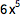
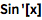
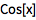

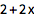
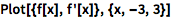
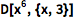
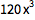
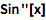
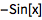
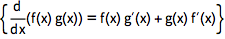

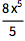
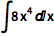
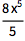
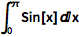
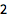

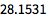
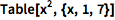
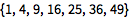
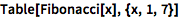
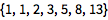

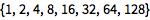
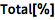
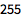
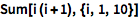
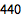

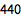

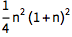

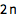
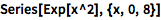
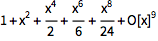
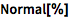
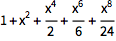
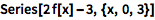
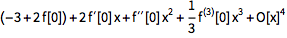
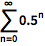
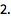
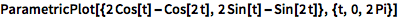
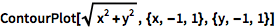
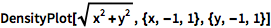
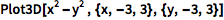


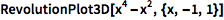
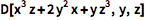
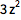

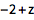
 .)
.)
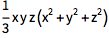

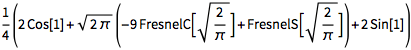
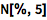
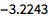
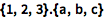
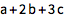
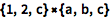
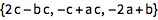
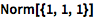
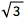
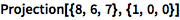
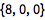
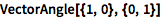
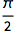

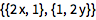

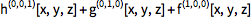
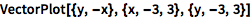


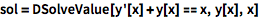
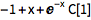
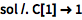
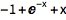

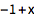


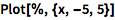
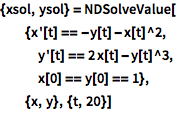

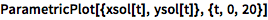
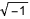 表示为 I:
表示为 I: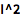
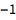
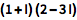
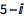
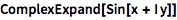
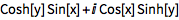
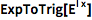
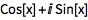
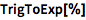
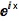
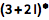
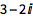
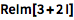
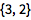
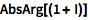
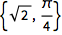



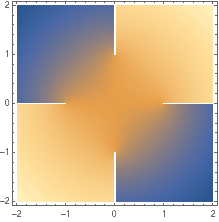
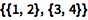
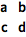
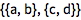
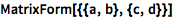
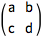
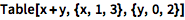
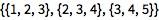
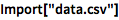
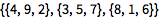
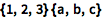
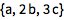
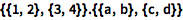
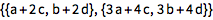
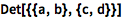
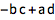
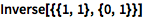
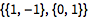
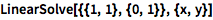
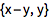

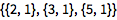
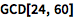
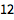
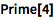
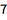

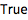
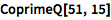
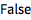
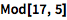
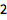

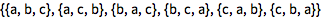

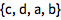
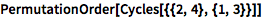
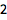


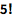
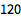

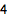
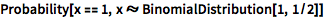
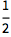
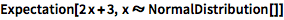
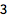

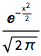
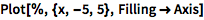


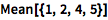
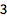
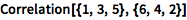
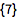
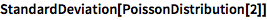
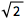
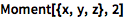
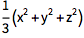
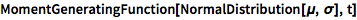
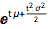


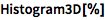
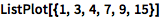
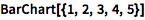

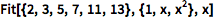
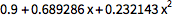

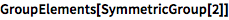

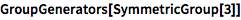
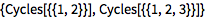


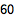
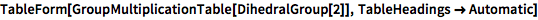
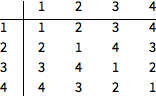

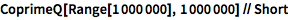
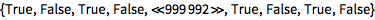

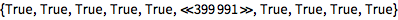

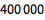

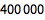

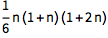

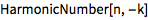

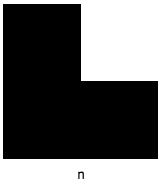







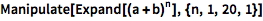
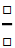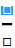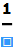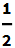
 符号,可用在键盘快捷输入形式
符号,可用在键盘快捷输入形式
 输入完成后,表达式就会发生改变:
输入完成后,表达式就会发生改变: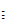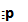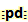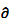

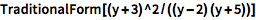
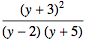
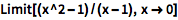
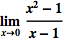
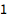
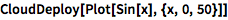
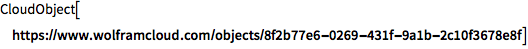

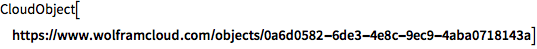





 浙公网安备 33010602011771号
浙公网安备 33010602011771号