数字图像处理(期末复习)
图像复原
图像复原与图像增强的异同点:
相同点:
图像增强与图像复原都是改善给定图像的质量。
不同点:
(1)图像复原需要建立图像的退化模型,再采用与退化相反的过程来恢复图像。图像增强不需要对图像降质过程进行建模
(2)图像复原改善图像的整体质量,图像增强改善图像的局部特性,例如:图像平滑与锐化
(3)图像复原是一个客观过程,有客观评价准则。图像增强适应人的心理、生理需要,很少涉及统一的客观评价准则。
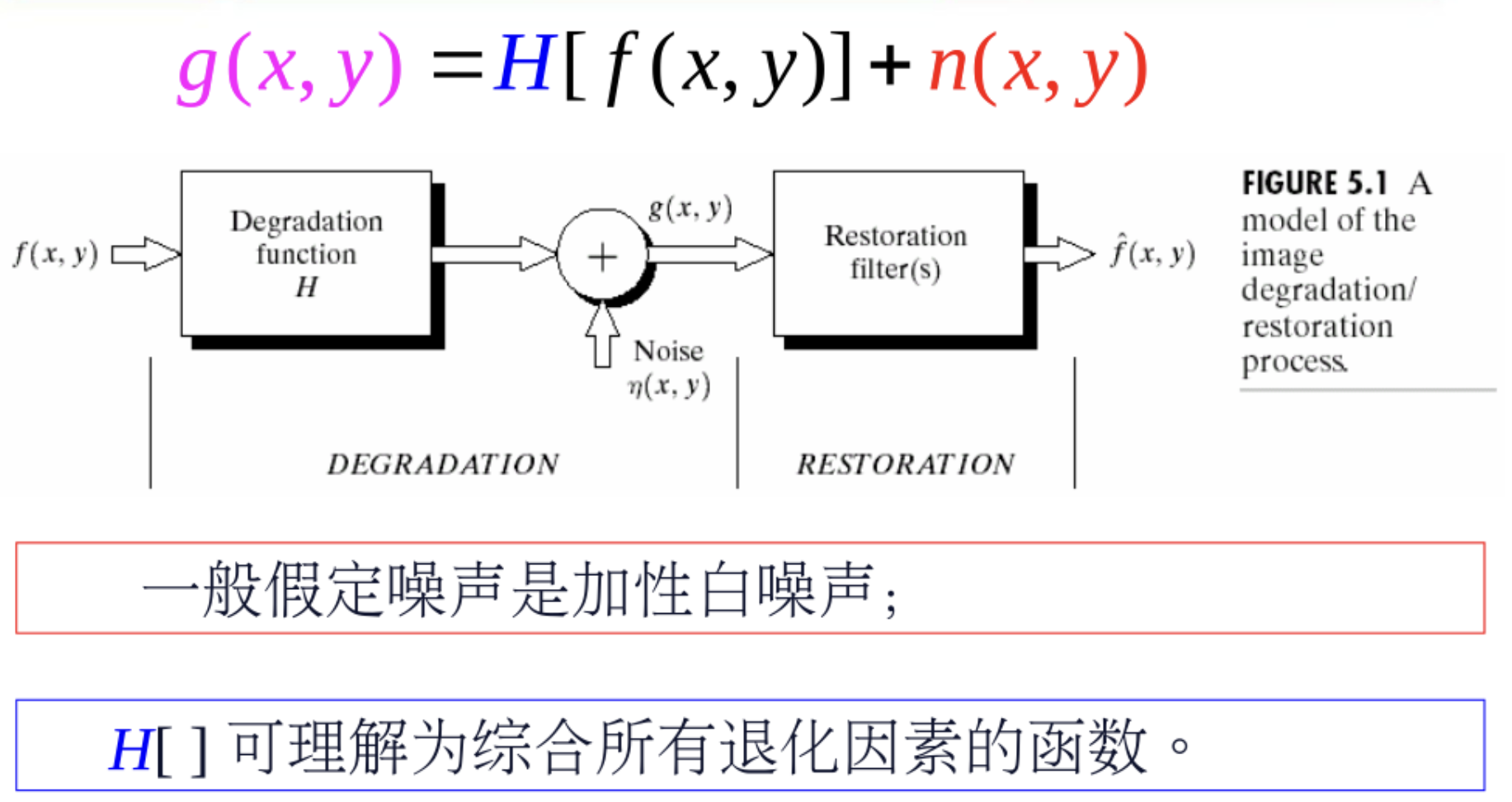
图像退化模型分析
f(x,y)是原图像的像素值
H()是降质函数
n(x,y)为随机噪声函数。
我们需要做的就是对质量较差的g(x,y)进行复原,得到\(\mathop f\limits^ \wedge\),真实生活里其实只有g(x,y)得到\(\mathop f\limits^ \wedge\),没有原图像f(x,y)进行比较。
既然要对图像复原,就必须要有滤波器,滤波器分为:
空间域滤波器:均值滤波复原、顺序统计滤波复原、自适应滤波复原
均值滤波复原:算术均值滤波器、几何均值滤波器、谐波均值滤波器、逆谐波均值滤波器
顺序统计:最大、最小、中点、修正alpha
频率域滤波器:带阻滤波器、带通滤波器、陷波滤波器、最佳陷波滤波器
均值滤波复原
算术均值滤波
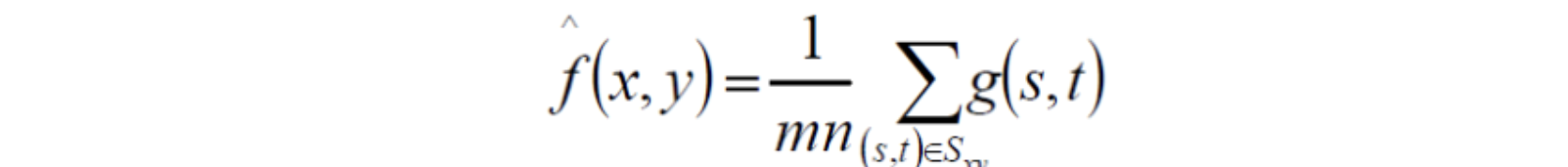
几何均值滤波
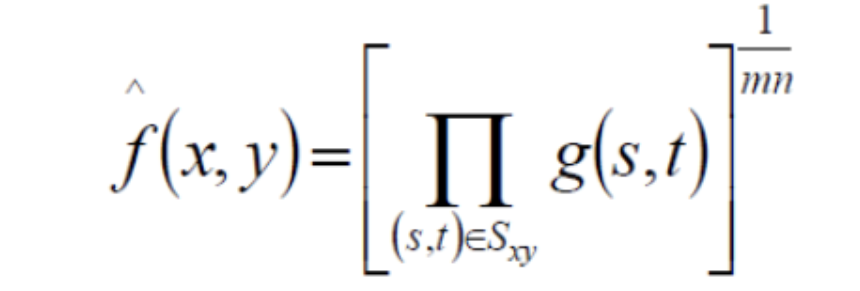
更好移除高斯噪声,对0噪声比较敏感
谐波均值滤波复原
对去除盐粒(白噪声)效果较好,不适用胡椒噪声。
原因:
\(\sum\limits_{({s_i},{t_j}) \in {S_{xy}}} {{1 \over {g({s_i},{t_j})}}} = {1 \over {g({s_1},{t_1})}} + {1 \over {g({s_2},{t_2})}} + ... + {1 \over {g({s_n},{t_n})}}\)
当g(s,t)其中一个为盐粒(接近255)噪声时,\({{1 \over {g({s_i},{t_j})}}}\)值其实很小,以至于对于整体和\(\sum\limits_{({s_i},{t_j}) \in {S_{xy}}} {{1 \over {g({s_i},{t_j})}}}\)变化其实很小,因此适合去除盐粒噪声,相反胡椒噪声就不行,因为会使\(\sum\limits_{({s_i},{t_j}) \in {S_{xy}}} {{1 \over {g({s_i},{t_j})}}}\)变化很大。
逆谐波均值滤波复原

证明:

简单理解就是:
当Q>0时,指数函数正相关,因此像素值越小,权重越小,和变化就越小,因此适合像素值较小的胡椒噪声。
当Q<0时,指数函数负相关,像素值越大,权重越小,和变化越小,因此适合权重较大的白盐噪声。
频率域滤波器
带阻滤波器:
理想带阻滤波器
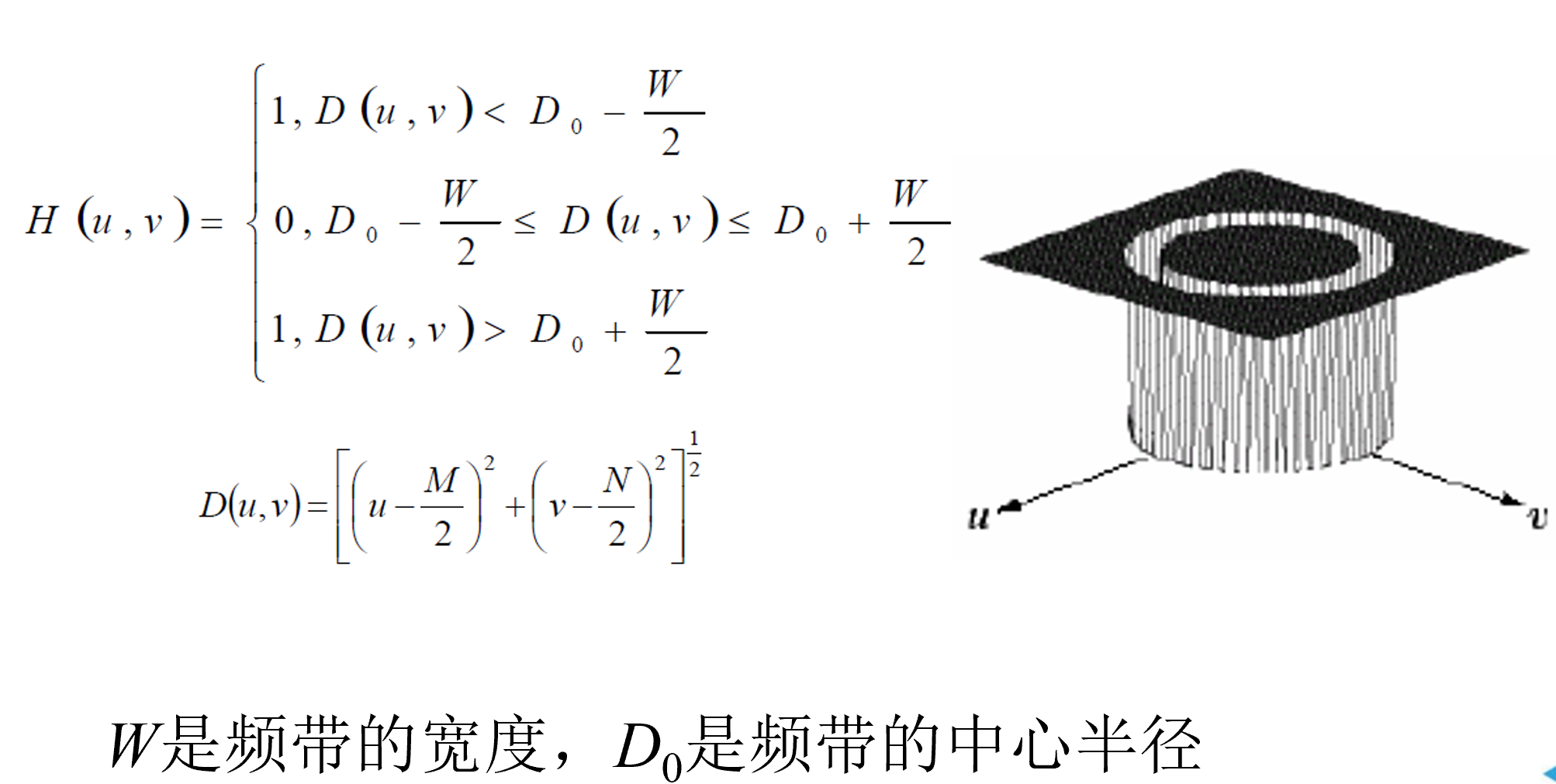
巴特沃斯带阻滤波
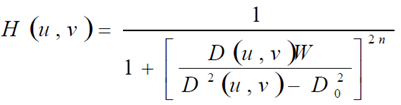
频率域带阻滤波器图像复原步骤:
首先确定频带的宽度W、频带中心半径D0
进行傅里叶变换F=fftshift(fft2(double(gray_image)));
%傅里叶变换
D(u,v)应该是u,v到中心图像(M/2,N/2)的距离
H(u,v)=1/(1+((D(u,v)*W)/(D(u,v)^2-D0^2))^(2*n));%巴特沃斯带阻滤波器
%应用滤波器
G=F.*H;
%计算逆傅里叶变换并恢复图像
restored_image=ifft2(ifftshift(G));
restored_image=uint8(restored_image);
%空间域卷积可以由频域乘积的反傅里叶变换得到
%f(x,y)h(x,y)<=F(x,y)*H(x,y)反傅里叶变换
%频率滤波-巴特沃斯带阻滤波器
Img_Ori=imread('33-orig.bmp'); %读取原始图像
Img_noise=imread('33-noise.bmp'); %读取噪声图像
W=300; %频带的宽度
D0=140; %频带中心半径
n=2; %阶数
gray_image=im2gray(Img_noise);
%傅里叶变换
F=fftshift(fft2(double(gray_image)));
%构建滤波器
[M,N]=size(Img_noise);
[u,v]=meshgrid(1:M,1:M);
%计算传递函数D
D=zeros(M,N);
H=zeros(M,N);
for u=1:M
for v=1:N
D(u,v)=sqrt((u-M/2)^2+(v-N/2)^2);
H(u,v)=1/(1+((D(u,v)*W)/(D(u,v)^2-D0^2))^(2*n));%巴特沃斯带阻滤波器
end
end
%应用滤波器
G=F.*H;
%计算逆傅里叶变换并恢复图像
restored_image=ifft2(ifftshift(G));
restored_image=uint8(restored_image);
%空间域卷积可以由频域乘积的反傅里叶变换得到
%f(x,y)h(x,y)<=F(x,y)*H(x,y)反傅里叶变换
图像几何变换
最近邻插值
最近邻插值原理:变换后的像素的灰度值等于它最近的输入像素的灰度值
涉及到的公式:
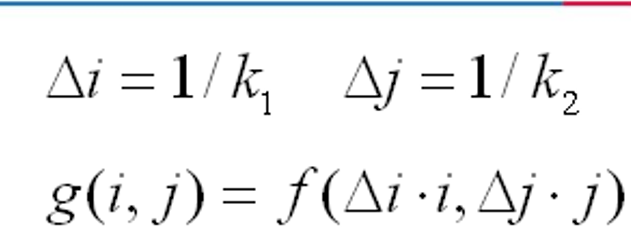
变换前尺寸:m与n
变换后尺寸:k1m与k2n
变换后的最大下标:k1mdelta(i)=m永远不会超过原图像下标,因此正确可行。
例题:
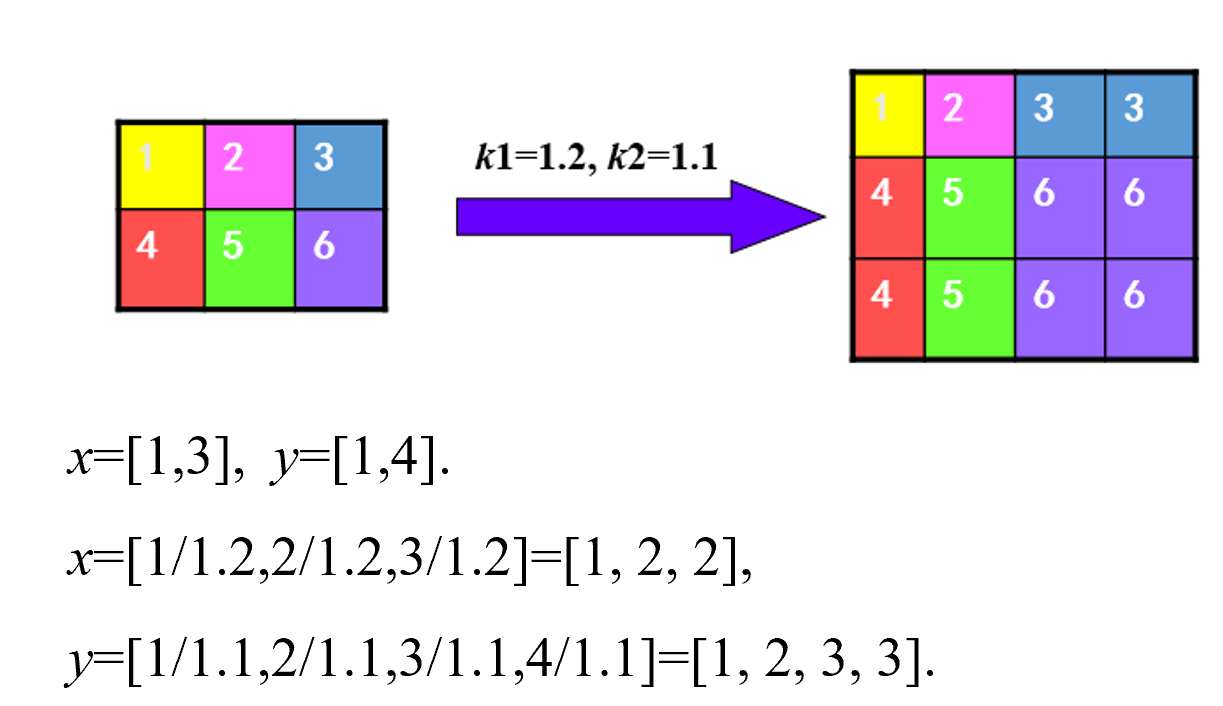
[m,n]=size(Img)=[2,3]
分别乘以扩大系数:
m=1.22=2.4向上取整=3
n=1.13=3.3向上取整=4
对于新图像:
1/k1=1/1.2=0.83
1/k2=1/1.1=0.91
(1,1)->(0.83,0.91)->(1,1)=黄色
(1,2)->(0.83,0.912)->(1,2)=粉色
(1,3)->(0.83,0.913)->(1,3)=蓝色
(1,4)->(0.83,0.91*4)->(1,4)=蓝色
依次类推,四舍五入求即可。
线性插值
线性插值原理:
求出的分数地址与像素点不一致时,求出周围四个像素点的距离比,根据比率,由4个邻域的像素灰度值进行线性插值。
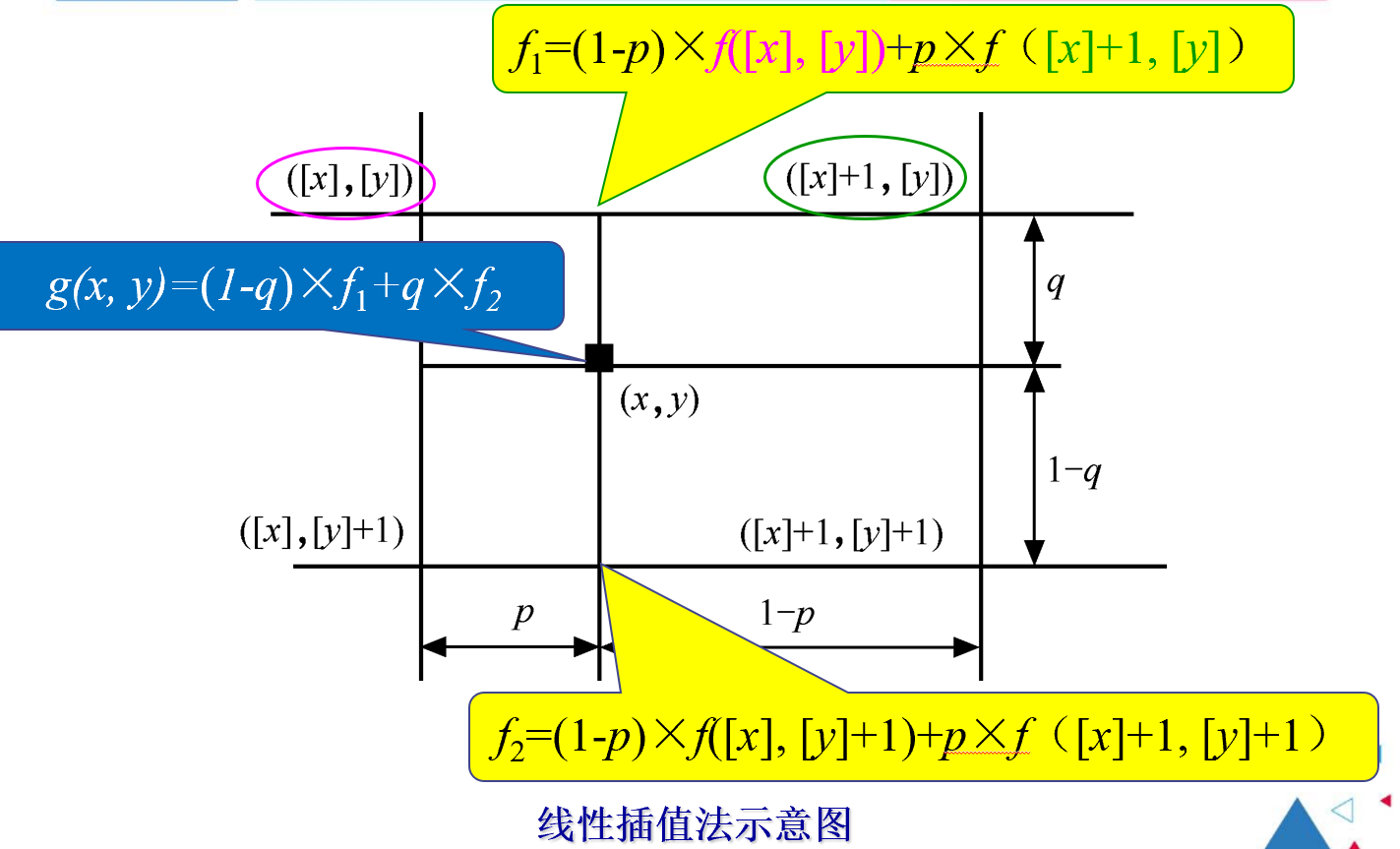
这个图里面的(x,y)是变换后的坐标:\(({\Delta _i}*i,{\Delta _j}*j)\),然后套公式计算。
这里[]为向下取整。例如:[3.2]=3
彩色图像处理
色度图:
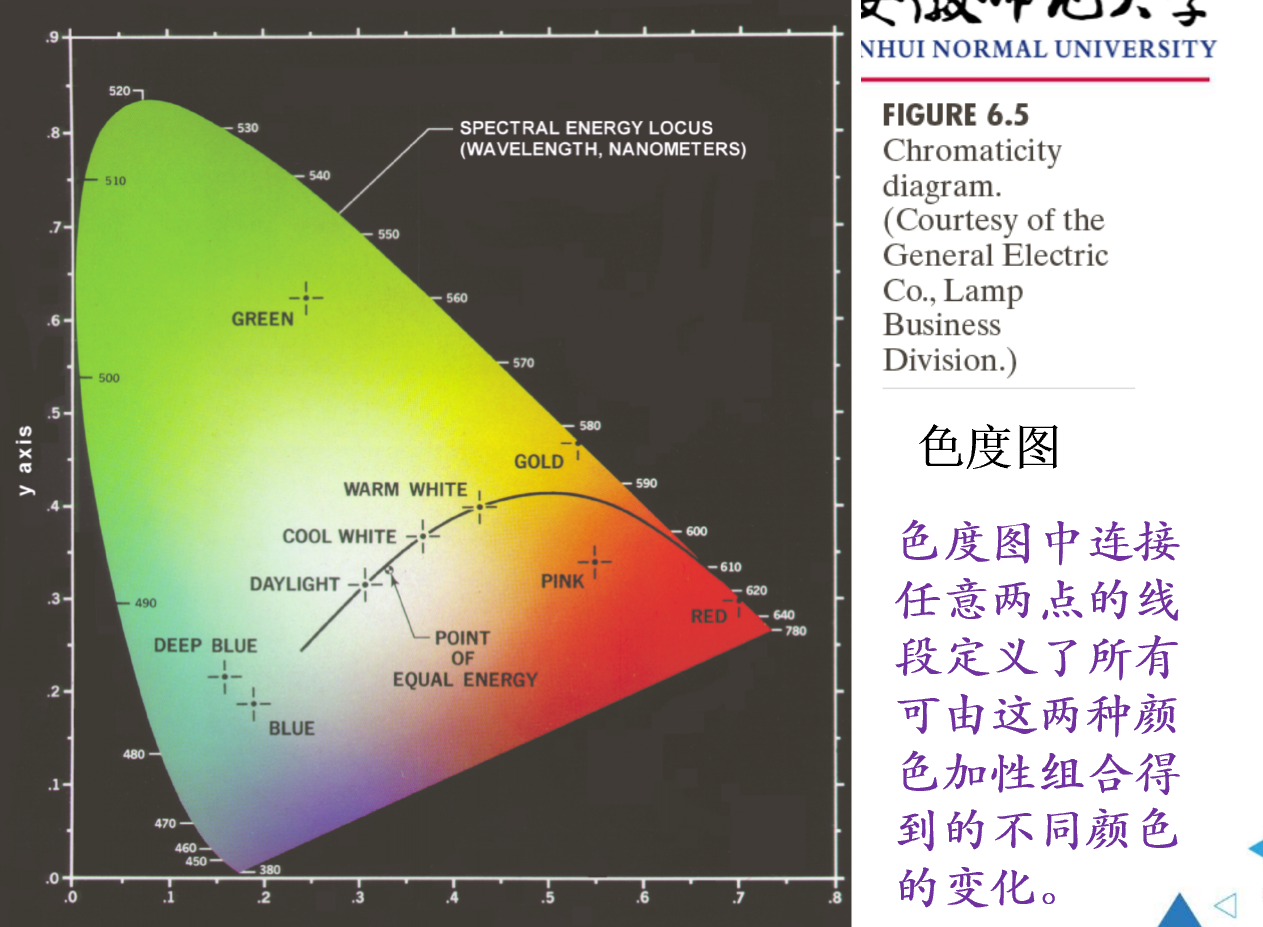
X轴代表R,Y代表G
任何一种颜色:c=xR+yG+(1-x-y)*B
例题:


什么是伪彩色图像处理?
伪彩色图像处理是将灰度图像映射到彩色空间的方法,突出兴趣区域或待分析的数据段。
彩色图像常用方式:灰度分层技术,灰度到彩色的变换
灰度分层技术
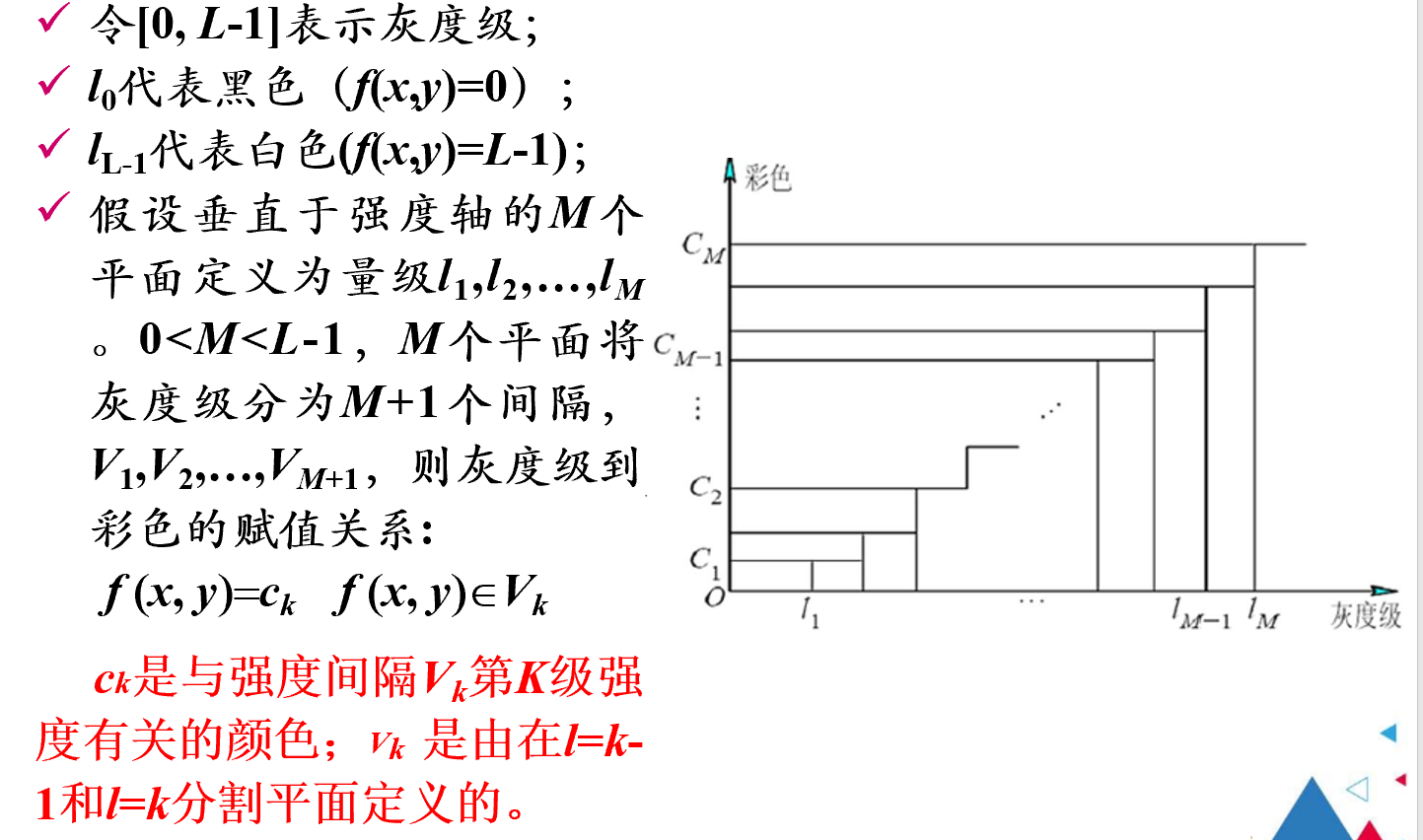
首先得到灰度值,按灰度值分层,不同层之间的灰度值赋值一个颜色。
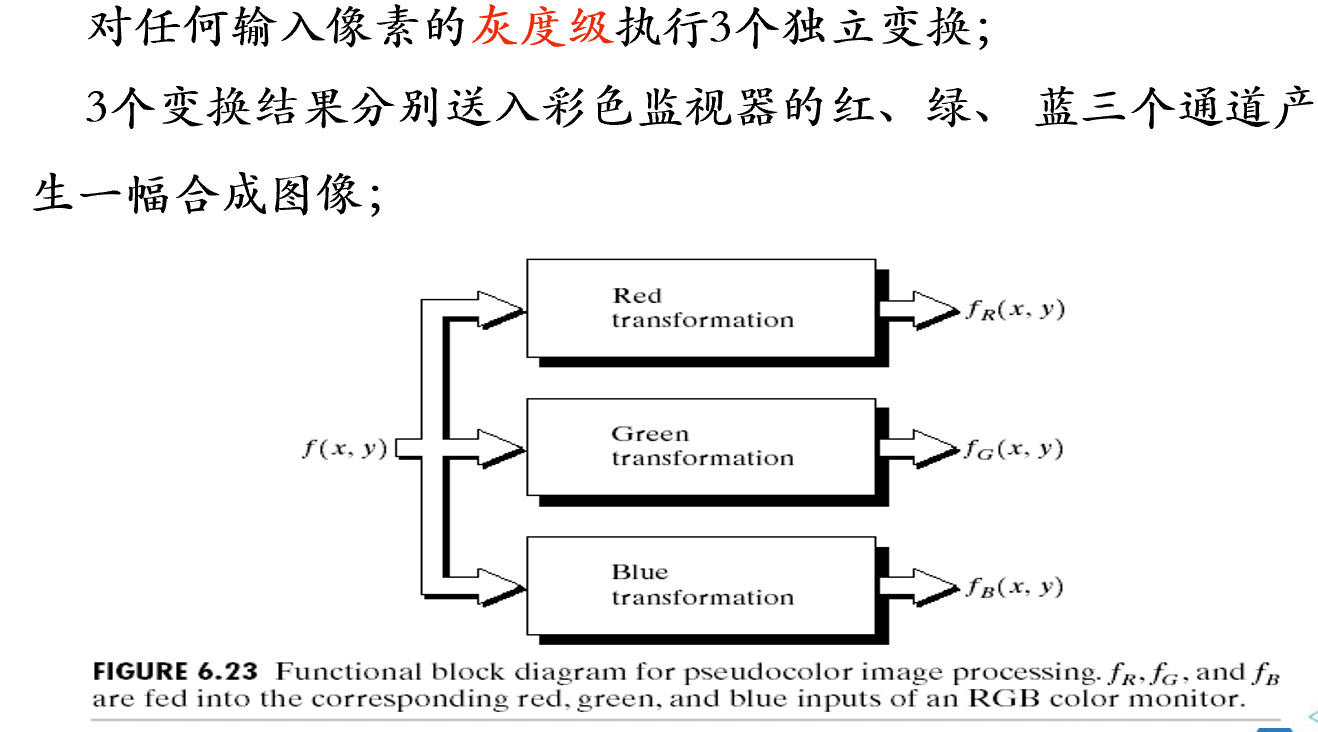
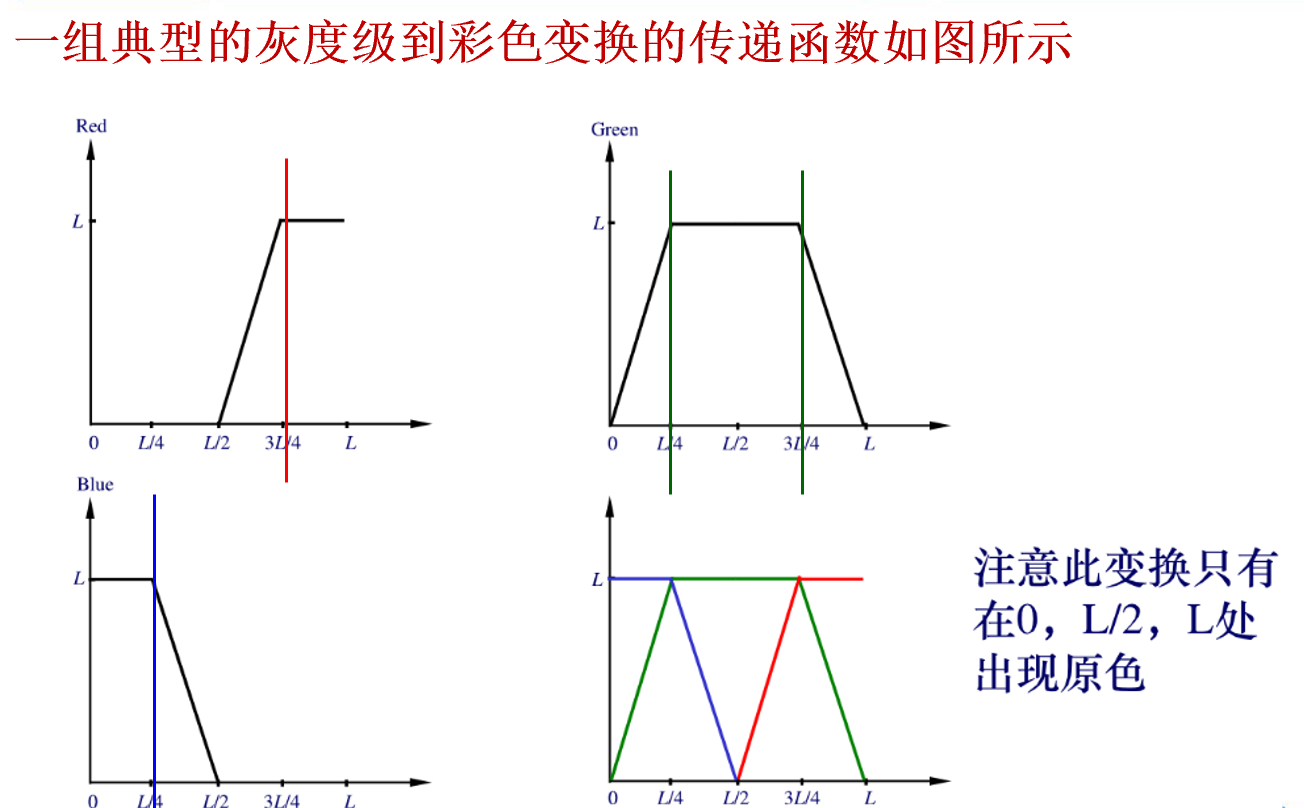
灰度到彩色的转换
对灰度值进行独立变换,R、G、B三个通道都要做一次变换,然后拼接在一起形成彩色图像1.
形态学图像处理
用途:简化图像数据,保持基本形状特性,出去不相干的结构。
运算操作:膨胀、腐蚀、开(先腐蚀后膨胀)、闭(先膨胀后腐蚀)
膨胀
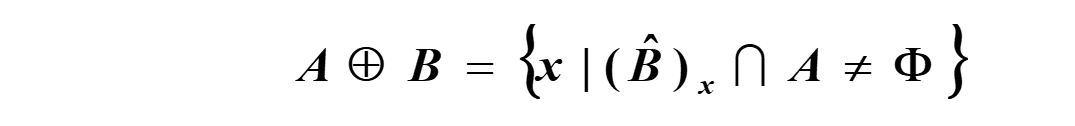
先对B结构元反射,然后将原点与像素对齐,有交集就置为1
例题:
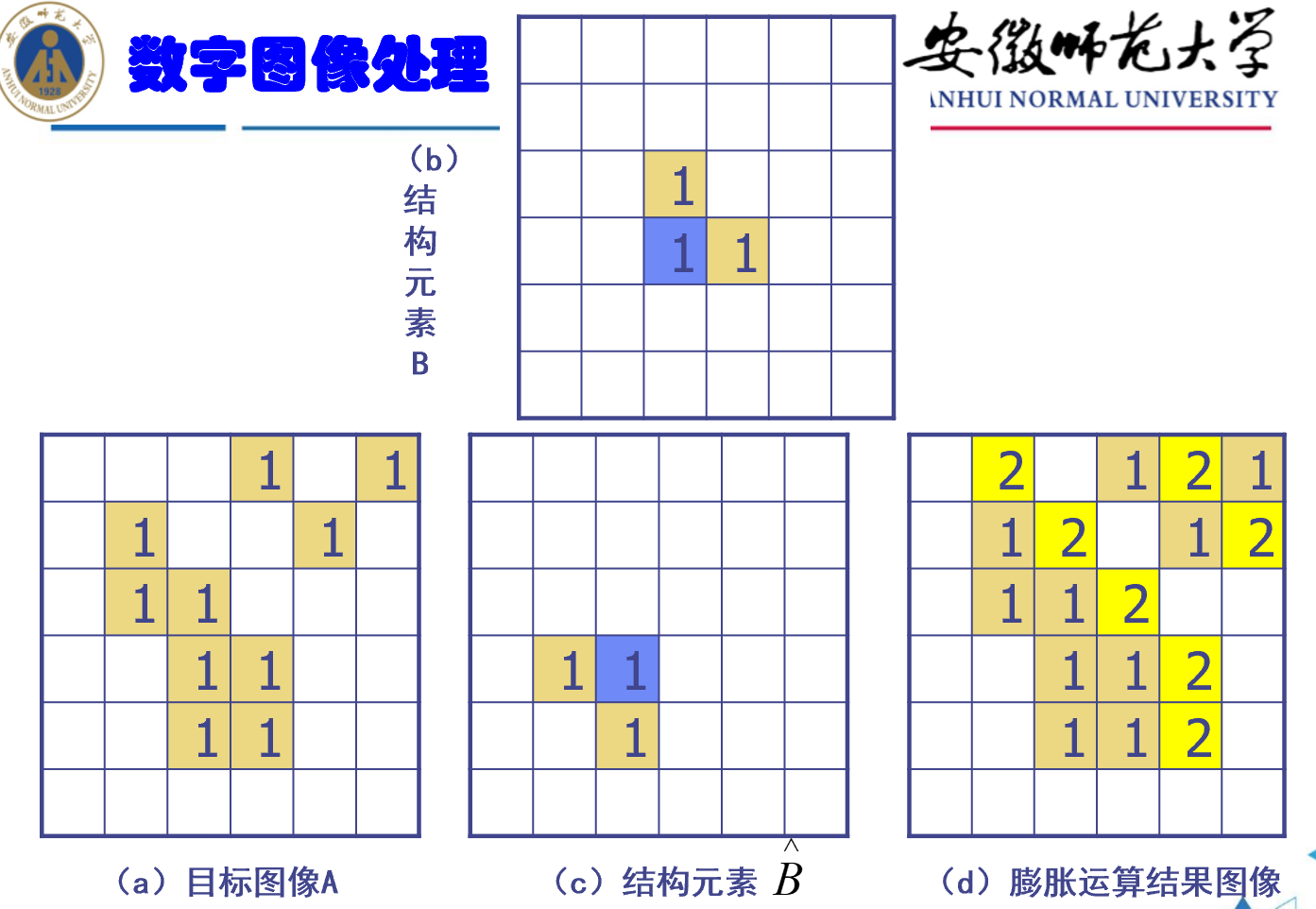
这里2代表新增加的像素,以区别1
可以出界
腐蚀
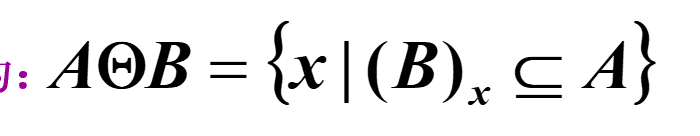
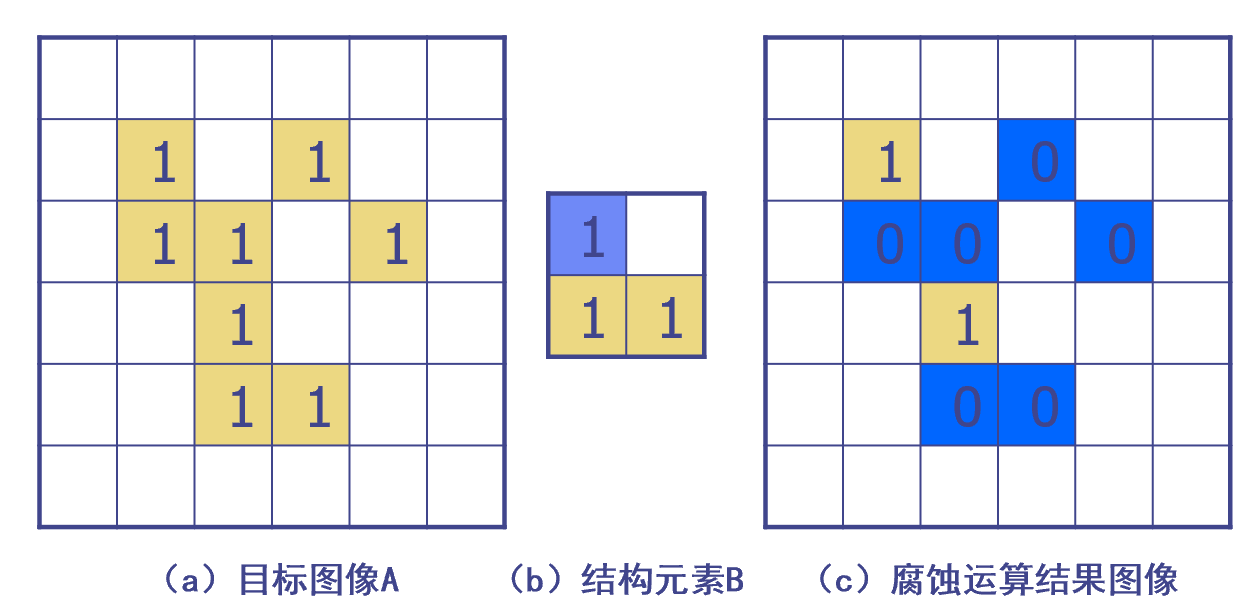
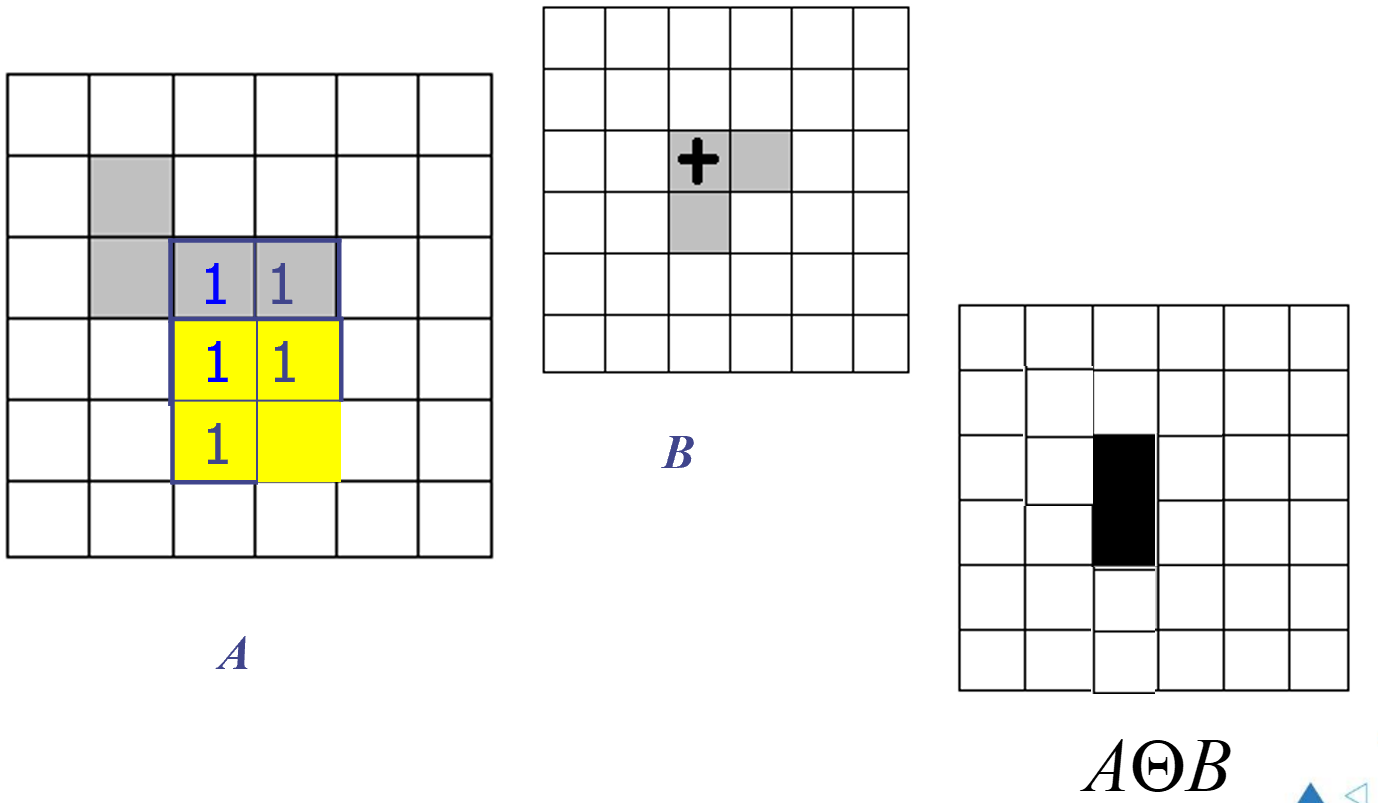
不可以出界
对偶性
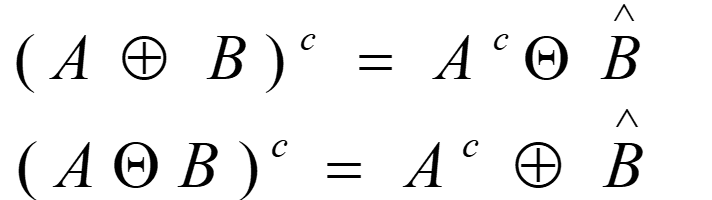
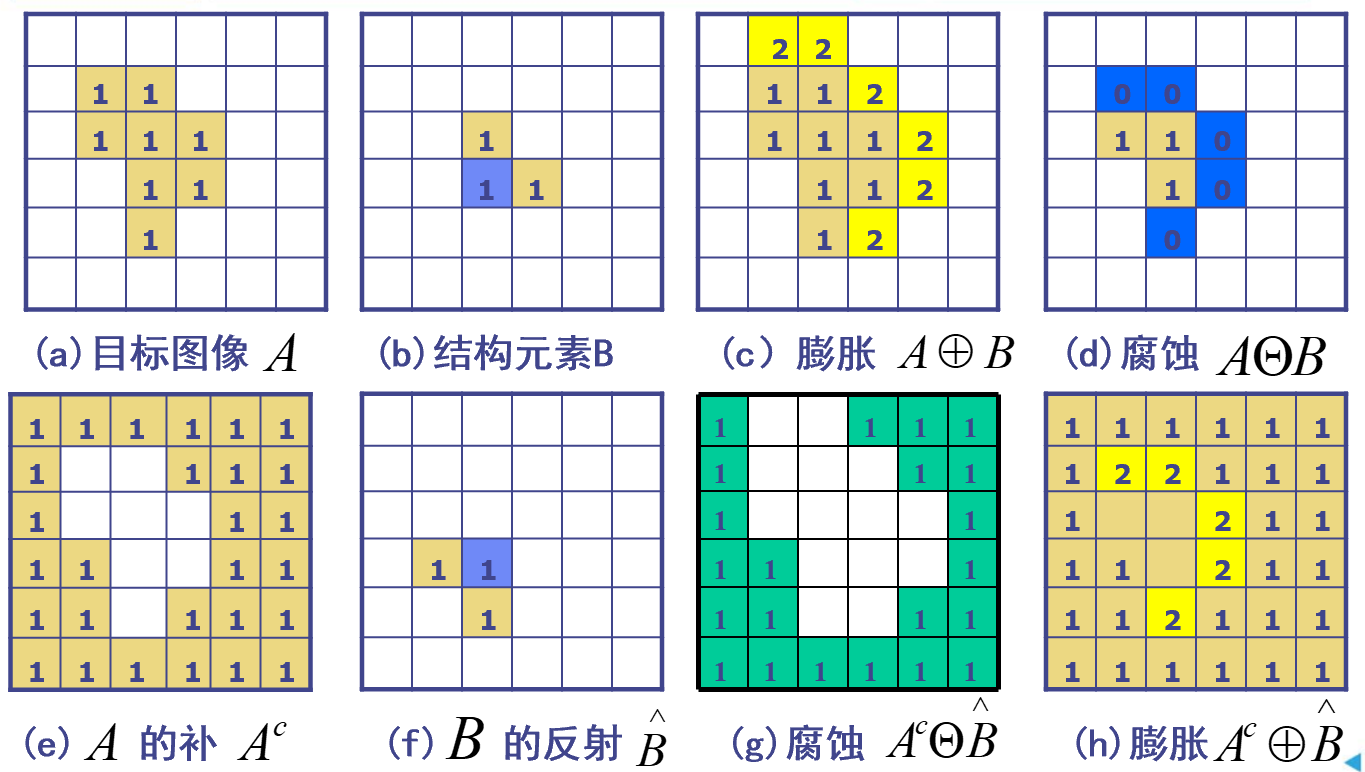
开操作
先腐蚀后膨胀
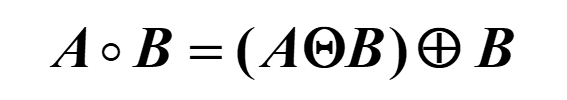
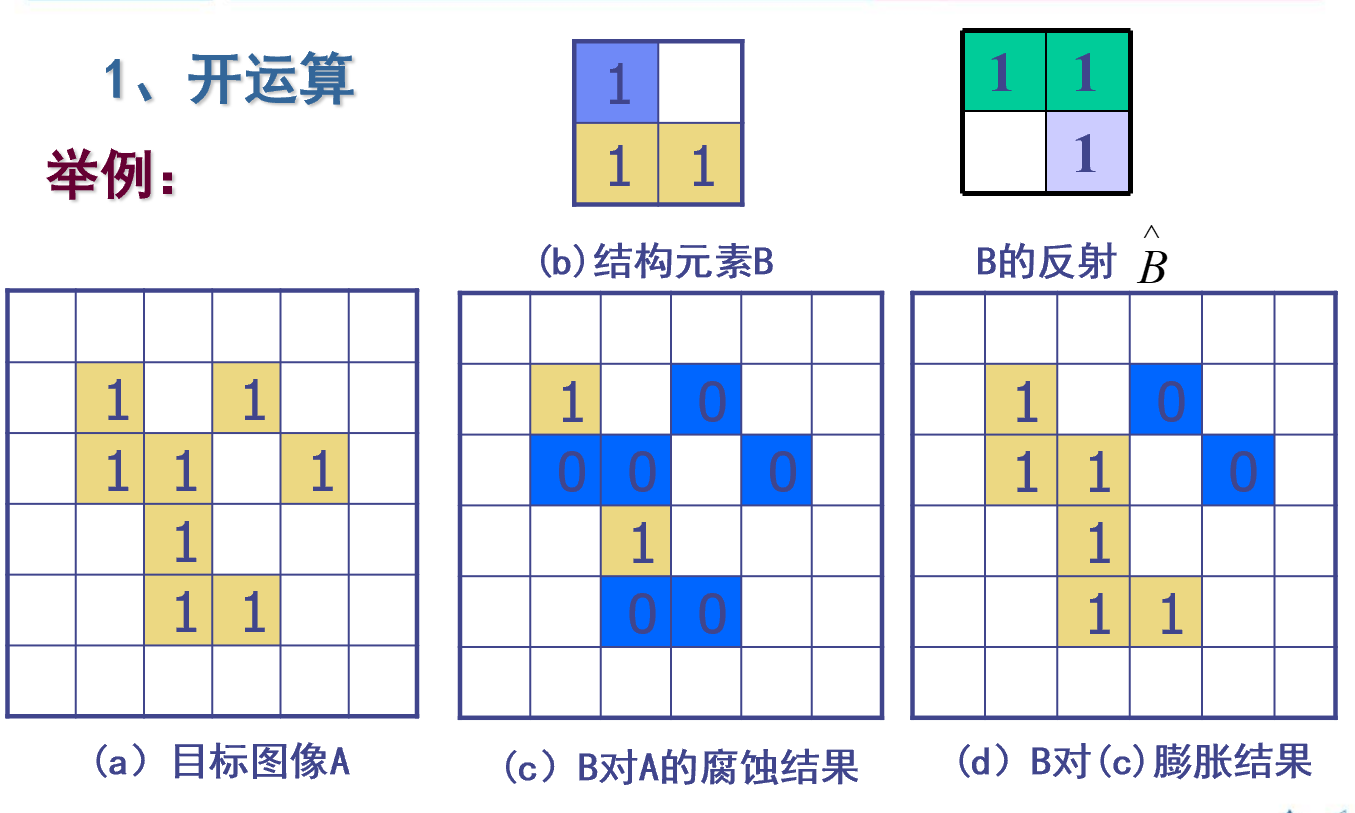
闭操作
先膨胀后腐蚀
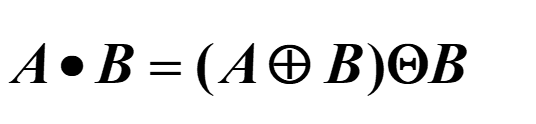
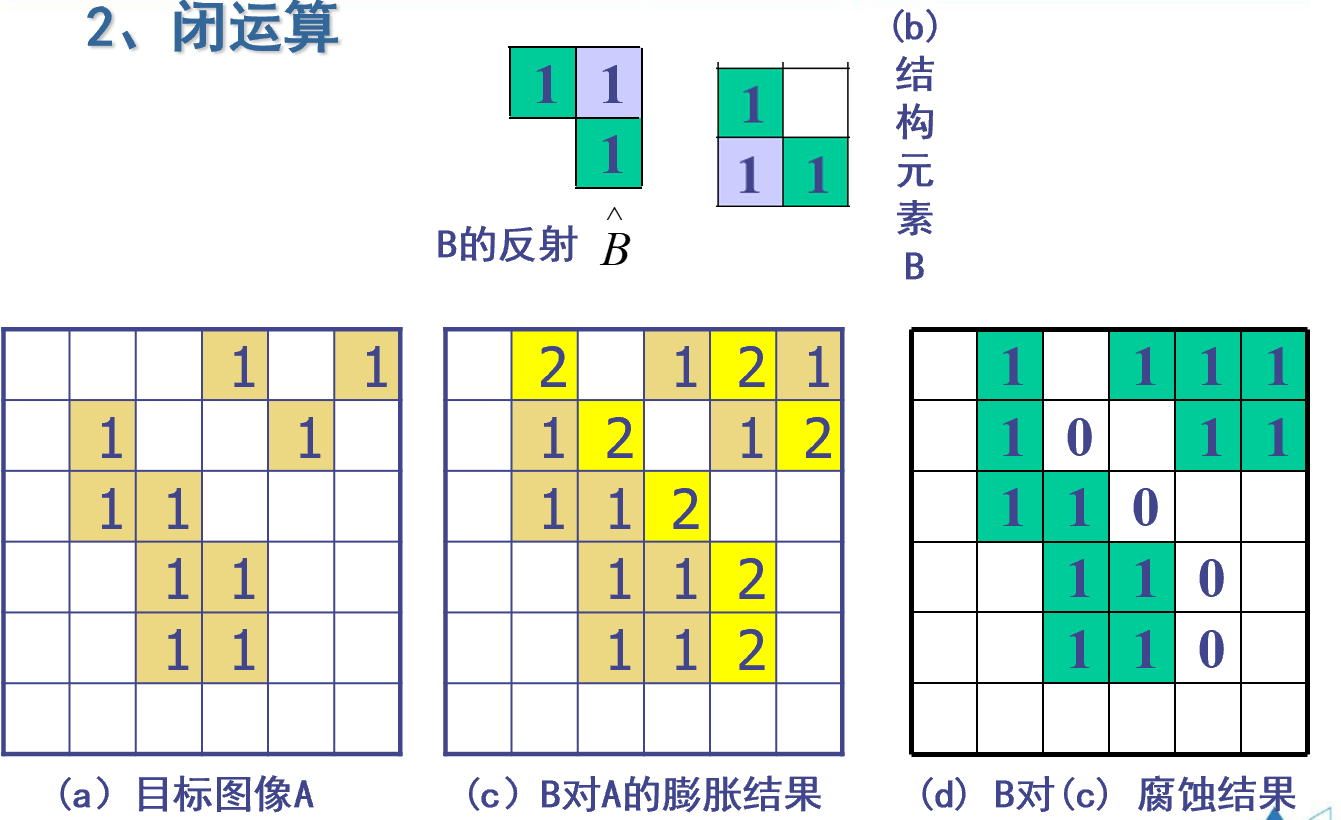
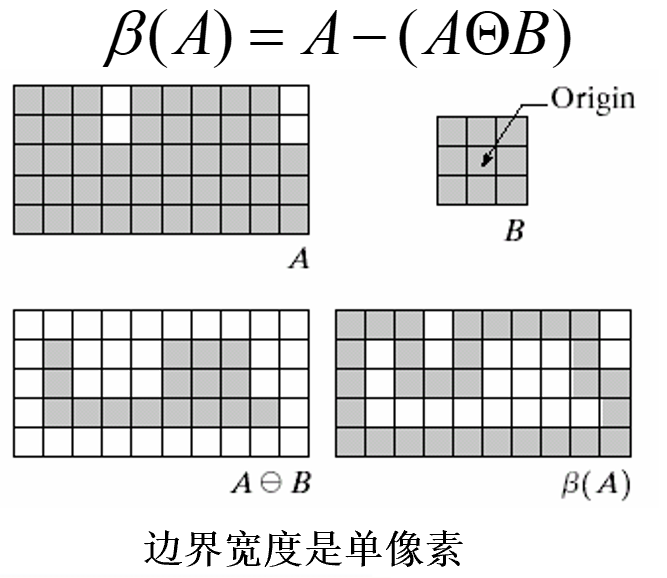
边界提取

区域填充
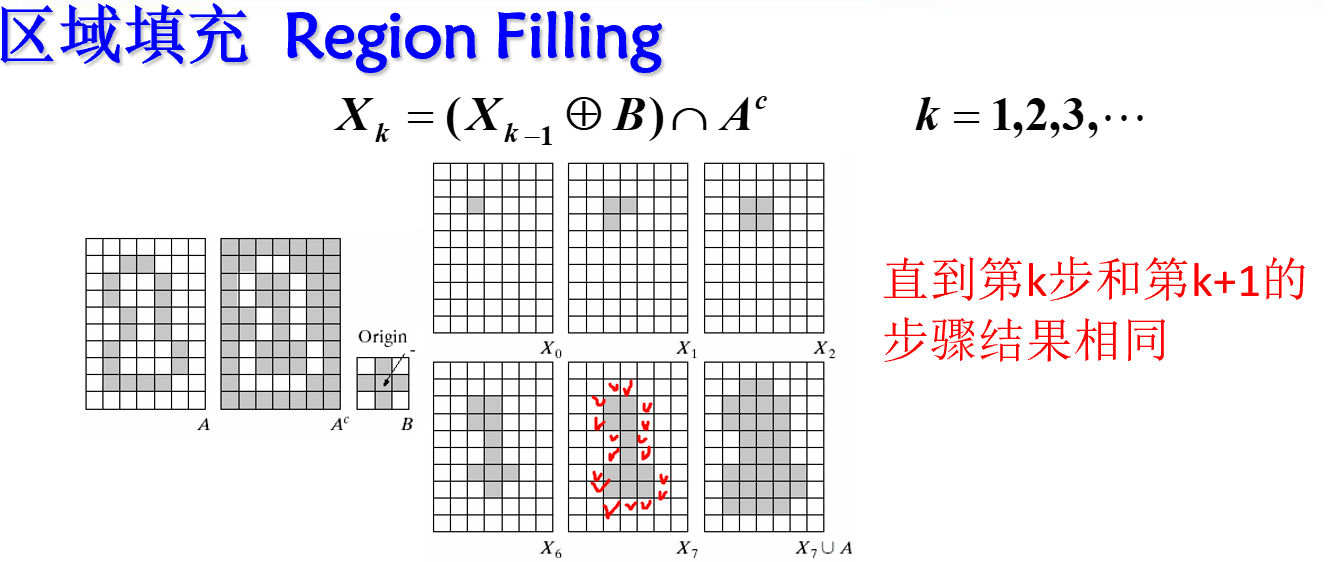
X_0里面随机挑一个点,用B结构元进行膨胀,再与A的补集进行与运算。
图像压缩
数据与信息的关系:
数据是信息传送的载体,相同的信息可以使用不同数量的数据表示
数据冗余类别
编码冗余



像素冗余


心理视觉冗余
主观:因人而异
图像压缩的目的
目的:满足一定的图像质量下,尽可能少的比特数表示原始图像,提高图像传输效率和减少图像的存储容量。
图像压缩技术的重要指标
指标有:压缩比、压缩算法、失真性
信息理论
信源符号为x_k,如果出现的概率为p_k,则x_k的信息量为:
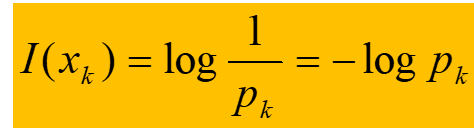
一个符号的p_k越小,不确定性越大,它的信息量越大
熵的概念
符号集中各个符号信息量的统计平均值,所有的信息量加起来除以信源符号的个数:
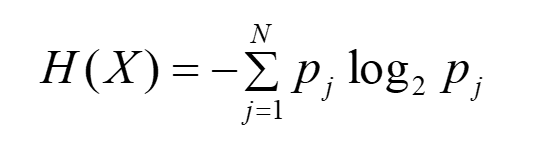
范围: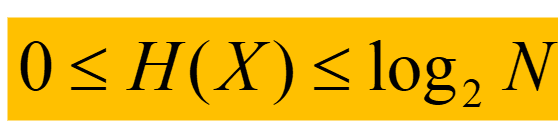
当p_i=1时,H(X)=0;
当p1=p2=...=p_n=1/N时,熵值最大(用拉格朗日约束证明)
用熵值来衡量是否为最佳编码:

什么意思?
首先使用熵值算法得到的压缩长度,是最理想的压缩长度,现实中不一定能够得到,因此作为一种参考标准
例题:


常用的图像压缩编码方法
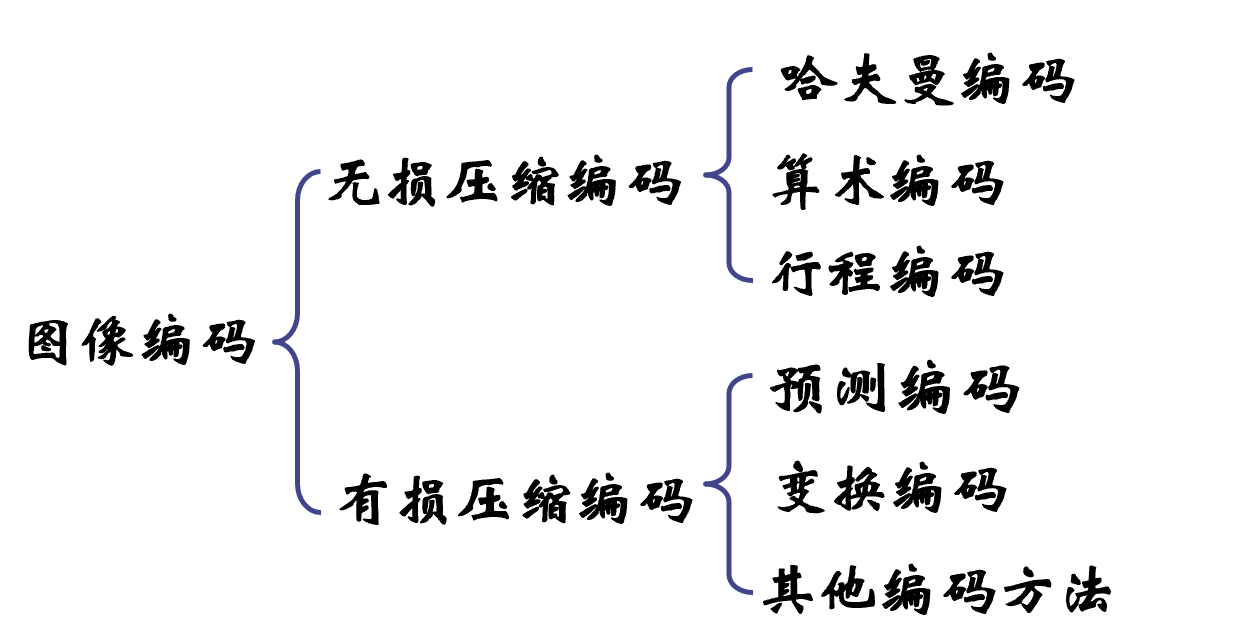
无损压缩编码

哈夫曼编码
哈夫曼编码利用信息符号概率分布特性的变长编码方法,概率大信息符号用短字节的码,概率小的信息符号使用长字节的码。

哈夫曼加权路径两种求法:
- 所有非叶子节点之和
- 叶子节点乘以他们所在的层数,第一层由根节点下面的层开始
例题:

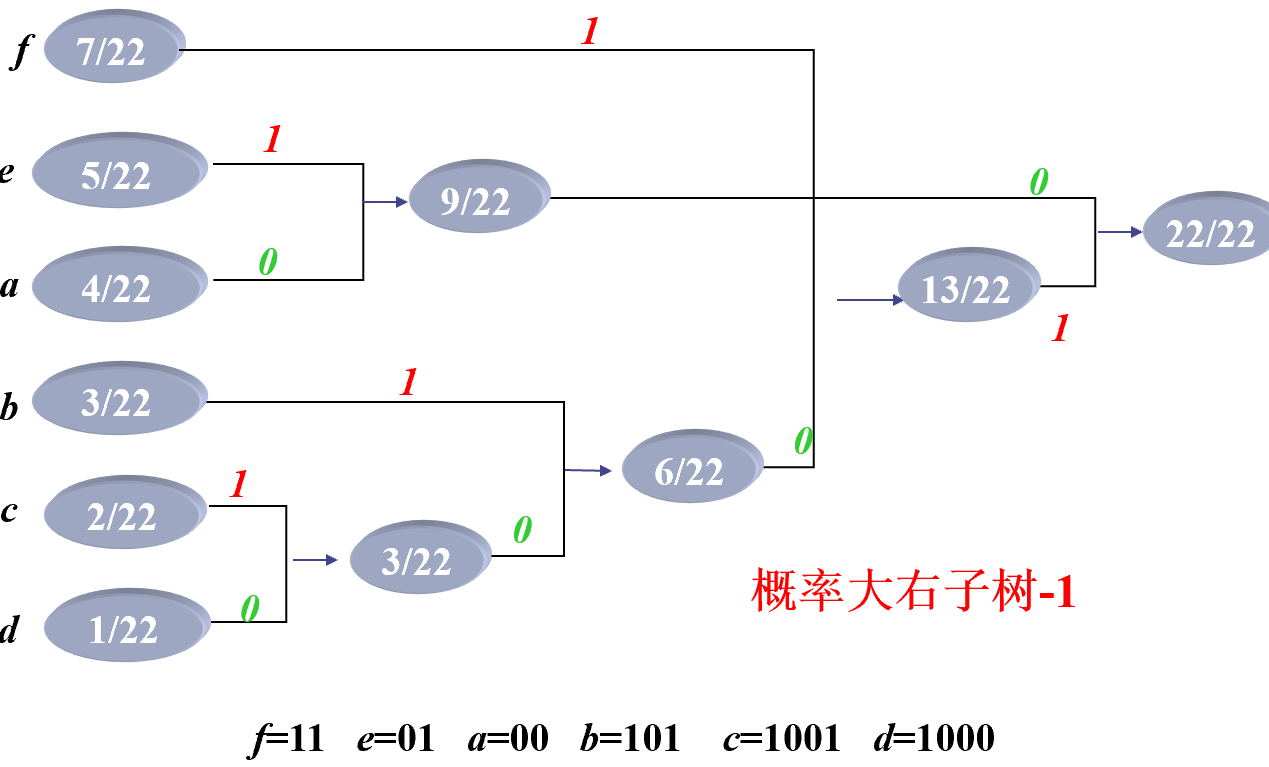

香农-费诺编码
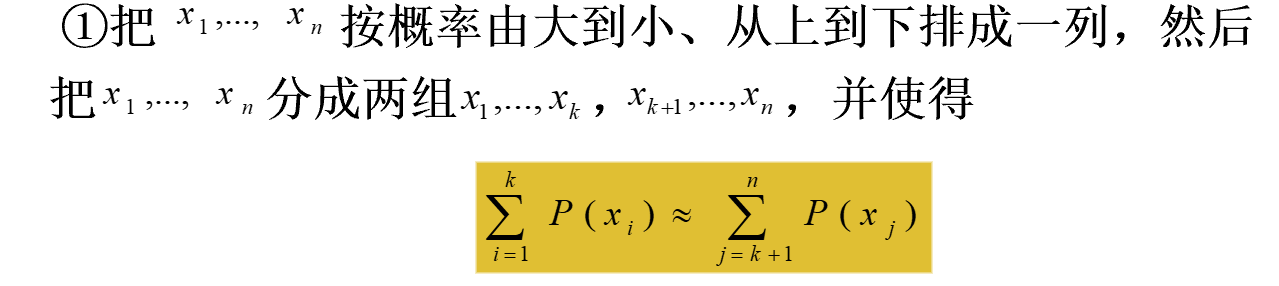
什么意思?
分成两半,使得两边的概率差最小。
例题:
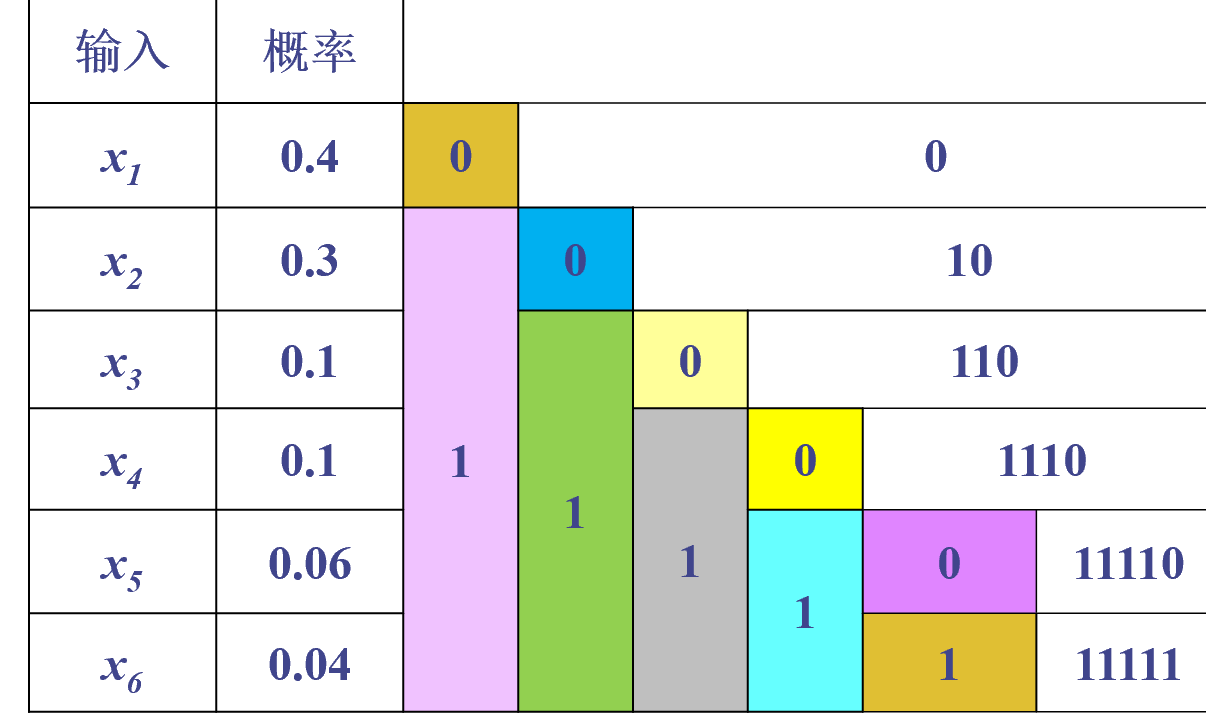

H(X)=-plogp正常算
算术编码
基本思想:

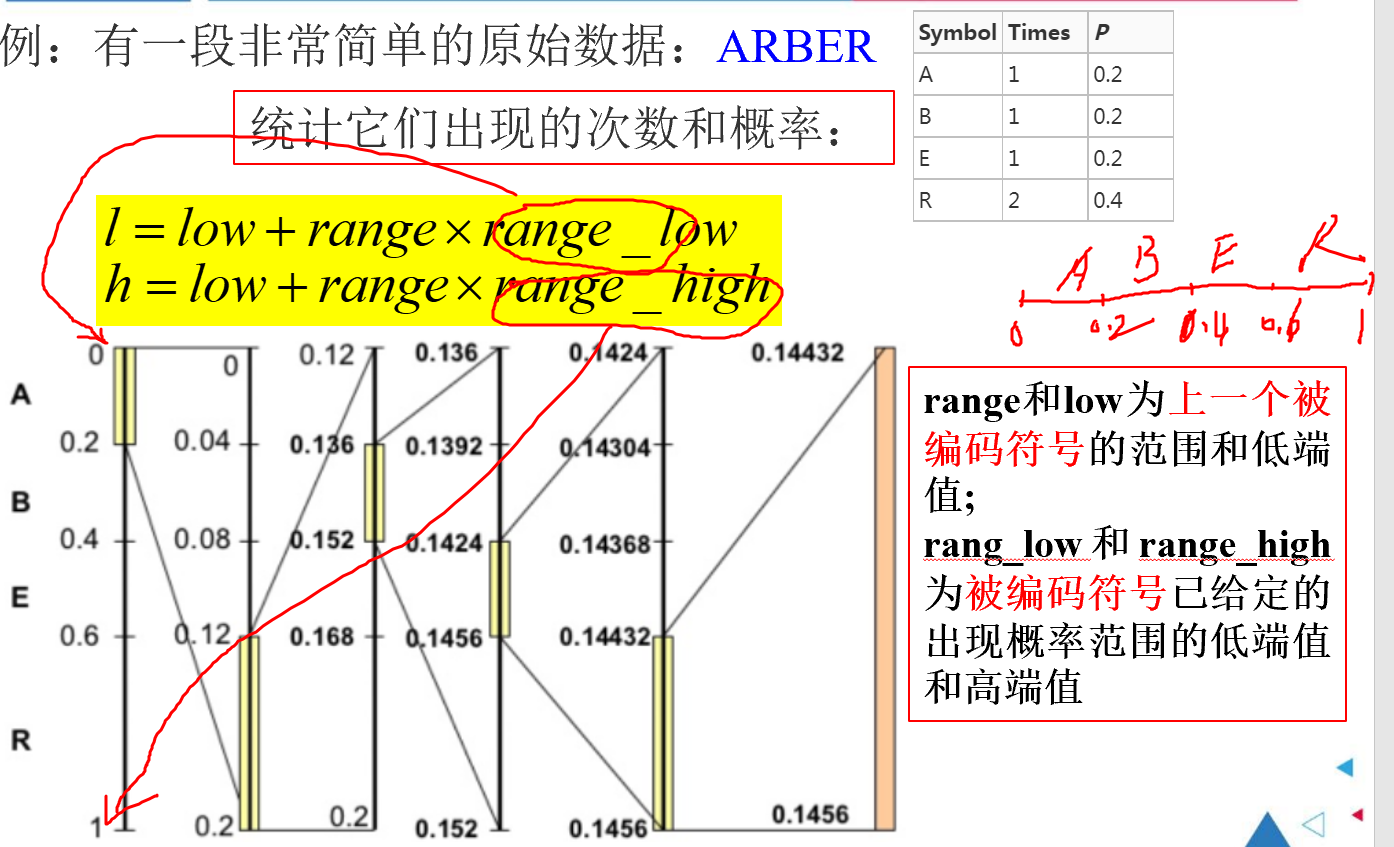
例题:
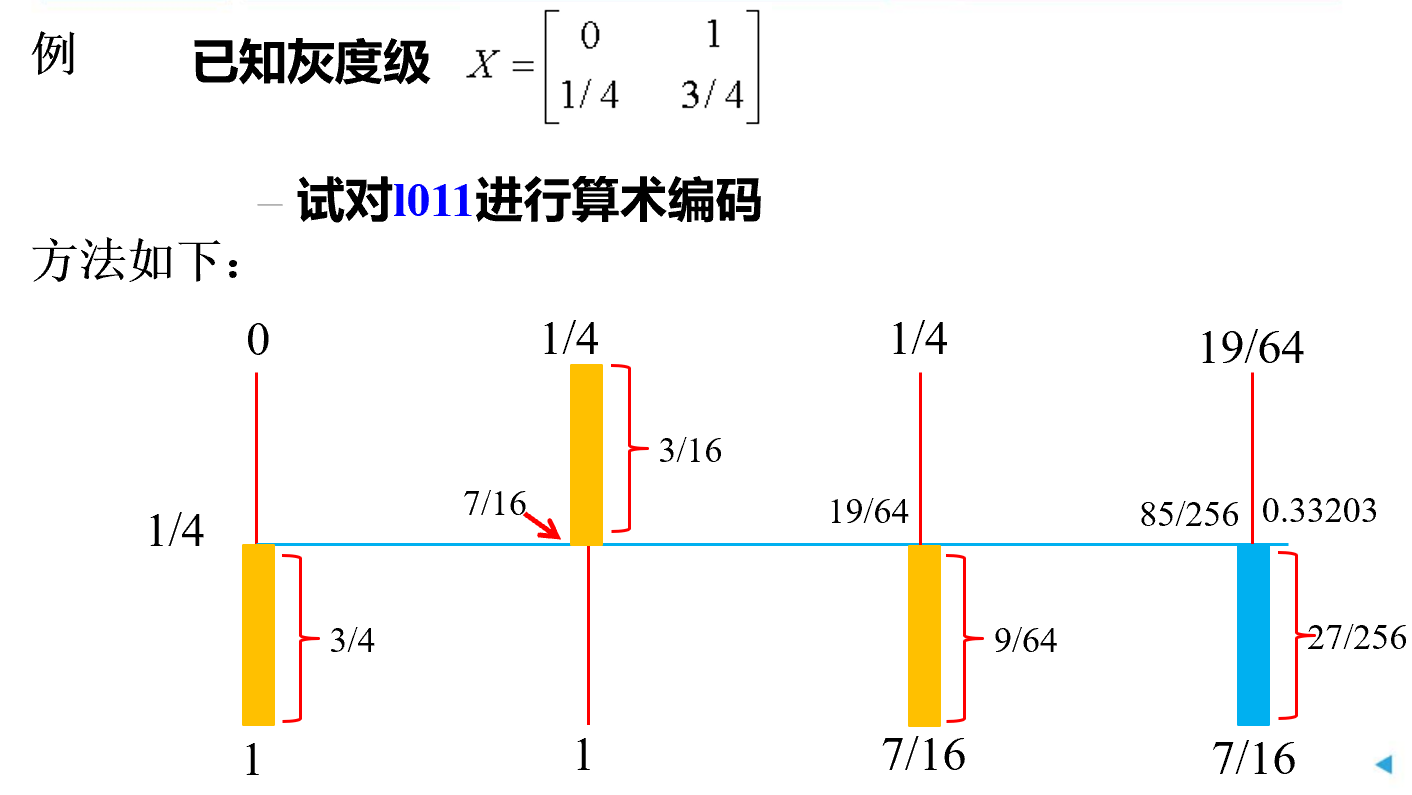
编码结果为子区间头尾之间取值。
解码:
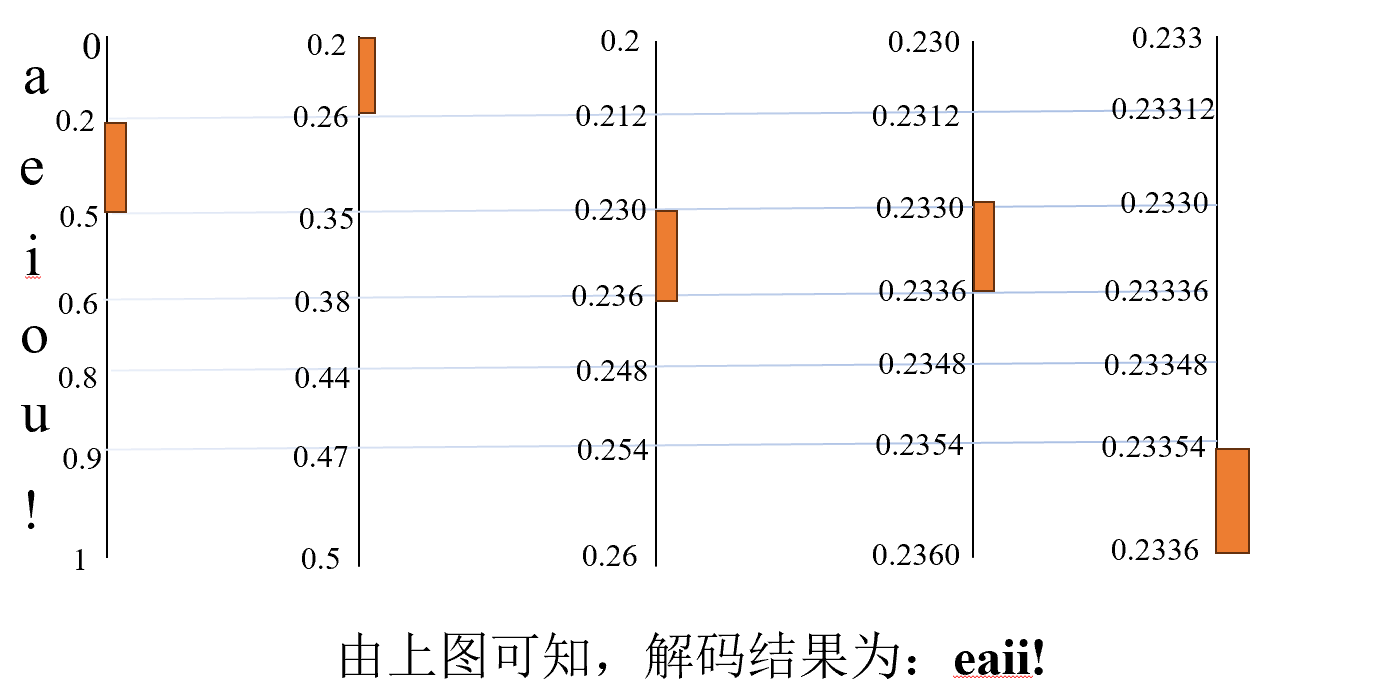

形成长度编码

有损压缩编码

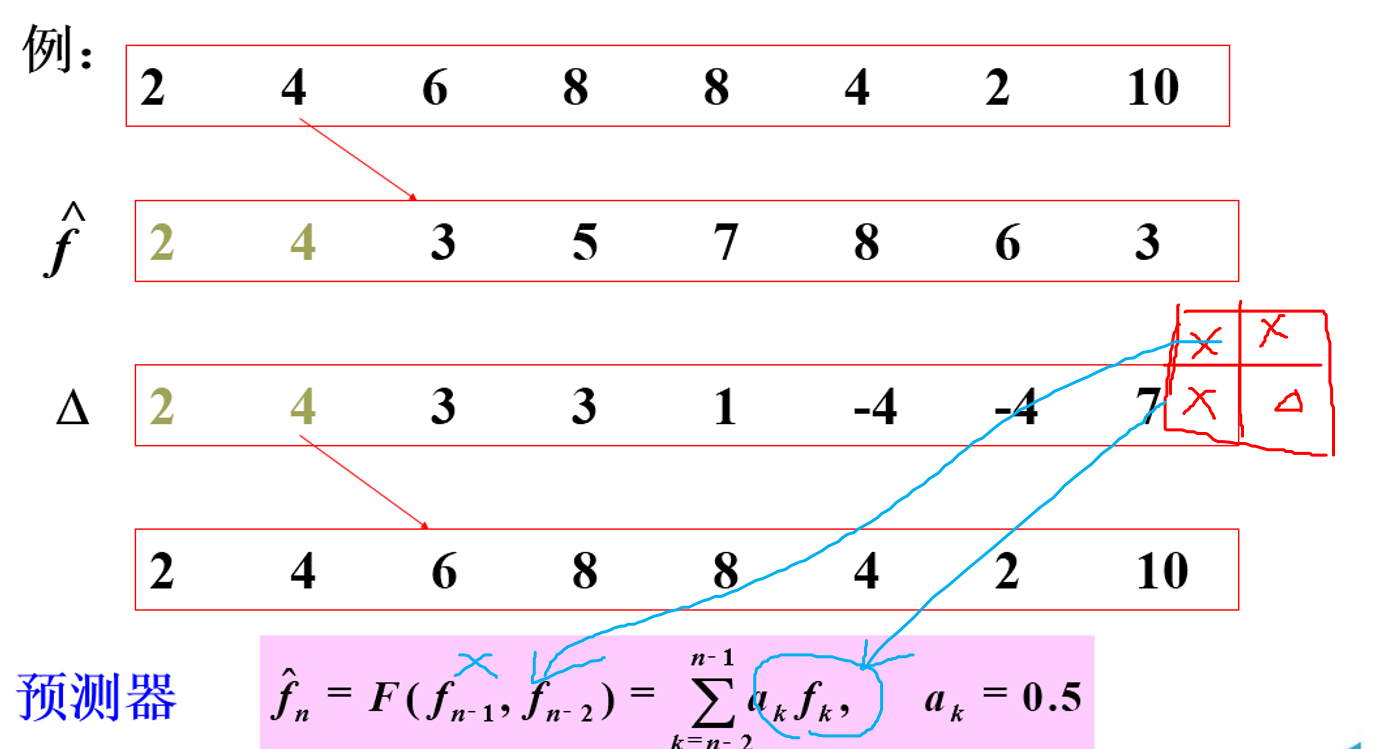
预测编码
图像分割
阈值分割
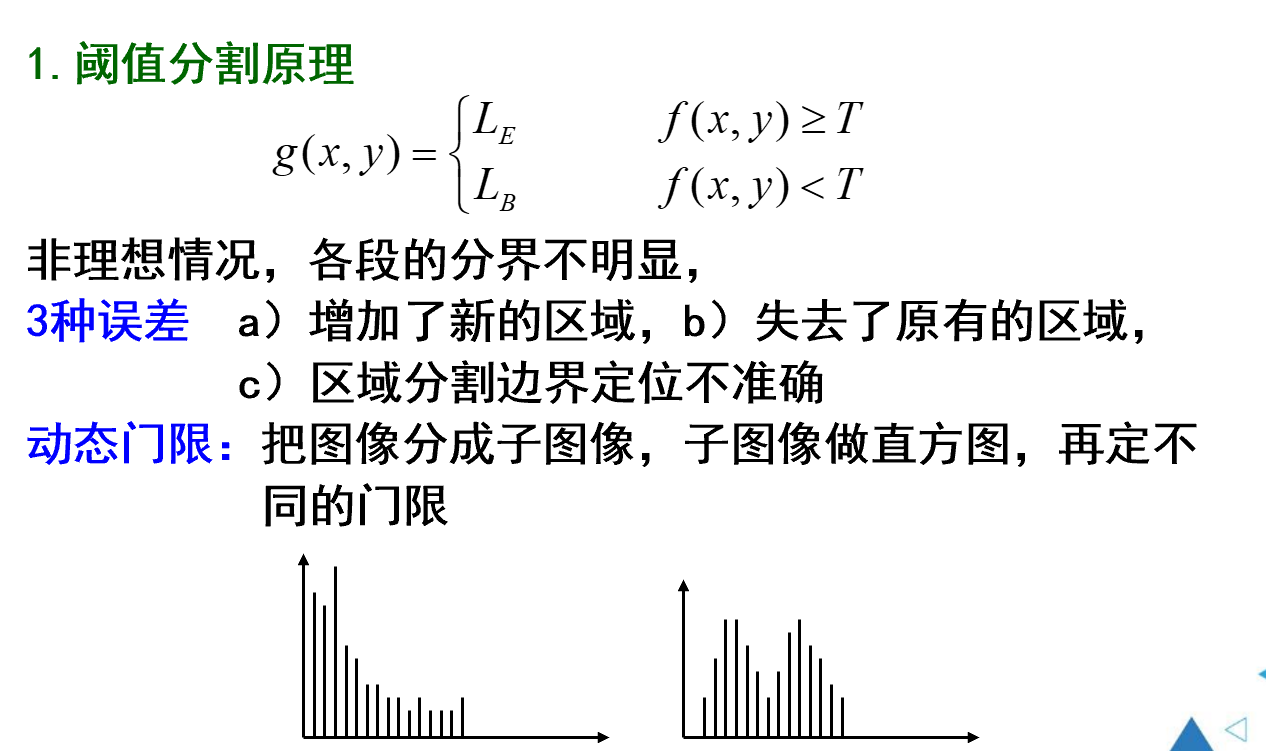
L_E和L_B分别表示目标与背景
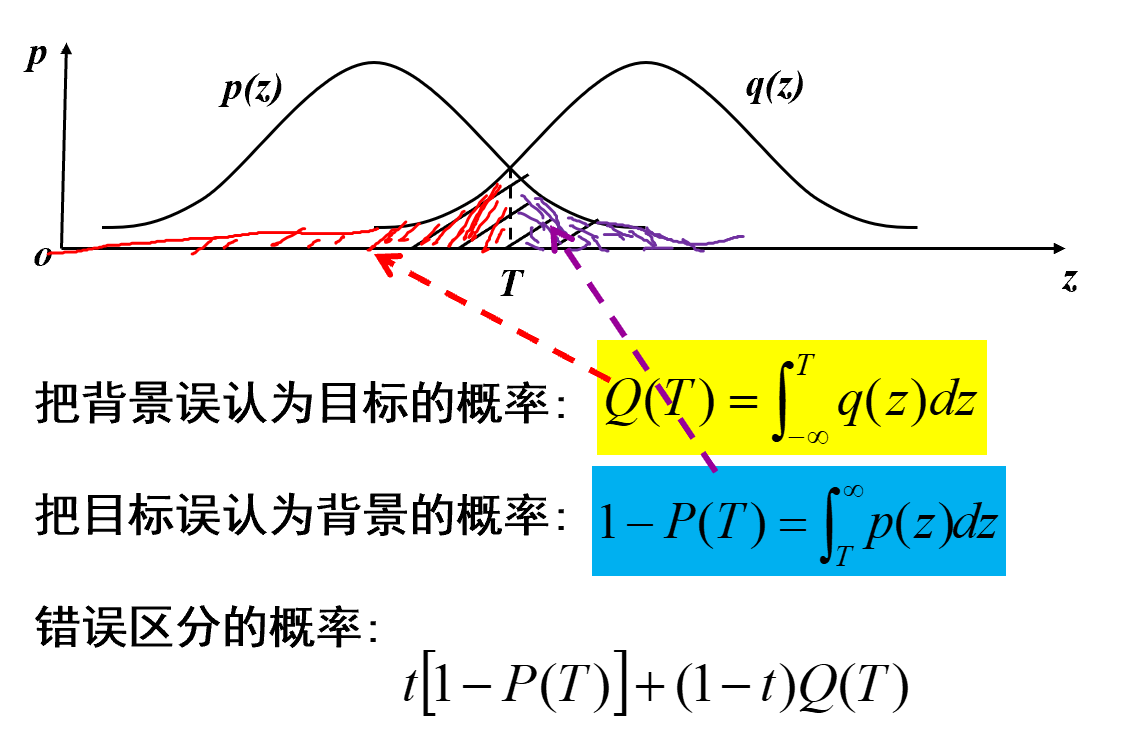
最小误差阈值值选取法
p(z)是目标,q(z)是背景
Hough变换的三个证明
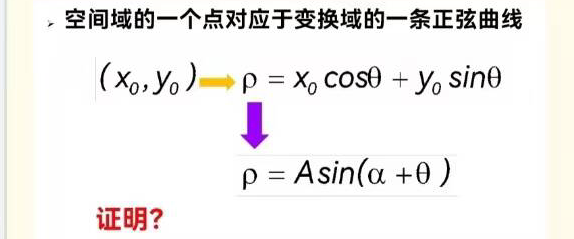
解答:
\(\eqalign{
& \rho = {x_0}\cos \theta + {y_0}\sin \theta \cr
& = \sqrt {x_0^2 + y_0^2} \sin (\alpha + \theta ) \cr
& \tan \alpha = {{{x_0}} \over {{y_0}}} \cr
& \cr}\)
高中背的三角函数公式:\(\sin (\alpha + \theta ) = \sin \alpha \cos \theta + \cos \alpha \sin \theta\)

解答:
\(\eqalign{
& {\rho _0} = x\cos {\theta _0} + y\sin {\theta _0} \cr
& \Rightarrow y = {{ - x\cos {\theta _0} + {\rho _0}} \over {\sin {\theta _0}}} \cr}\)
待定系数法,得到:$\left{ {\matrix{
{\alpha = - {1 \over {\tan {\theta _0}}}} \cr
{b = {{{\rho _0}} \over {\sin {\theta _0}}}} \cr
} } \right.\(

**解答:**
**将**\){y_i} = \alpha {x_i} + b\(**代入:**\)\rho = {x_i}\cos \theta + {y_i}\sin \theta\(**,得到:**
\)\eqalign{
& \rho = {x_i}\cos \theta + {y_i}\sin \theta \cr
& = {x_i}\cos \theta + (\alpha {x_i} + b)\sin \theta \cr
& = {x_i}(\cos \theta + a\sin \theta ) + b\sin \theta \cr}\(
**令**\)\cos \theta + a\sin \theta = 0\(**得到:**
\)\left{ {\matrix{
{{\theta _0} = - \arctan {1 \over \alpha }} \cr
{{\rho _0} = b\sin {\theta _0}} \cr
} } \right.\(
**因此每一条正弦曲线都过**\)({\rho _0},{\theta _0}) = (b\sin {\theta _0}, - \arctan {1 \over \alpha })$这一点。
这里参考高中数学解析几何过定点问题,例如**y=k(x-1)+2**,虽然k值在变,但是直线依然恒过(1,2)这个点。
制作人:LTQ
时间:2024.5.12夜

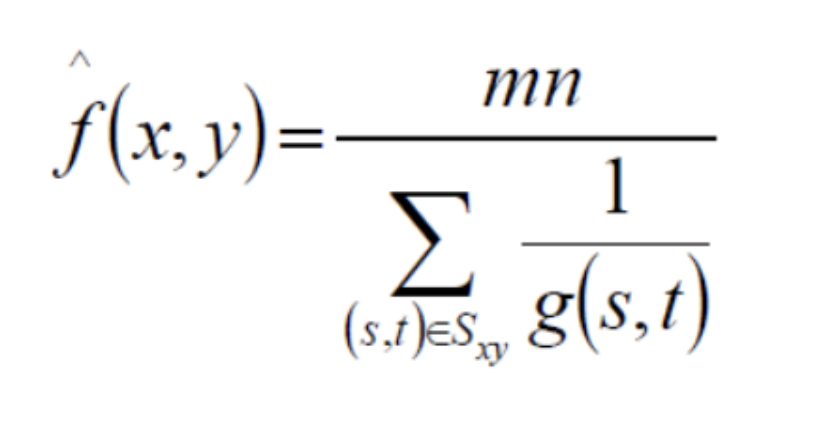

 浙公网安备 33010602011771号
浙公网安备 33010602011771号