10后都能看的懂的三大入门排序算法、冒泡排序、简单选择排序、直接插入排序

1、前言

1.1为什么要先谈这三个排序算法？

这三个排序算法是排序算法中最简单、最容易实现的。而且运用的思想在我们生活中常用，所以我们会很容易的去了解其基本思想。

2、冒泡排序（bubble sort）

2.1、什么是冒牌排序？

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。[1]
在经过n此扫描交换后即可将元素按照某种逻辑排序。

2.2、什么是扫描交换？

从一组数据中从前向后依次检查每一对相邻元素，一旦发现逆序即交换二者的位置。对于长度为n的序列，共需做n - 1次比较和不超过n - 1次交换，这一过程称作一趟扫描交换。[2]

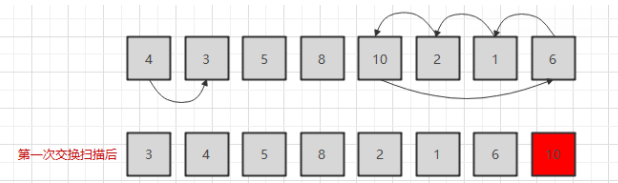
2.3、基本原理

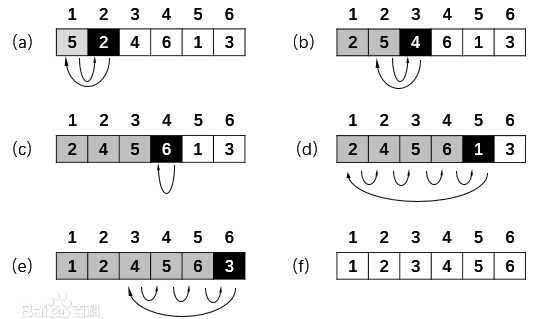
我们从图中发现，每经过一次扫描交换后局部有序就会增加一个元素，当局部有序中的元素的数量和整组数据中的元素数量相同的时候，排序就完成了。

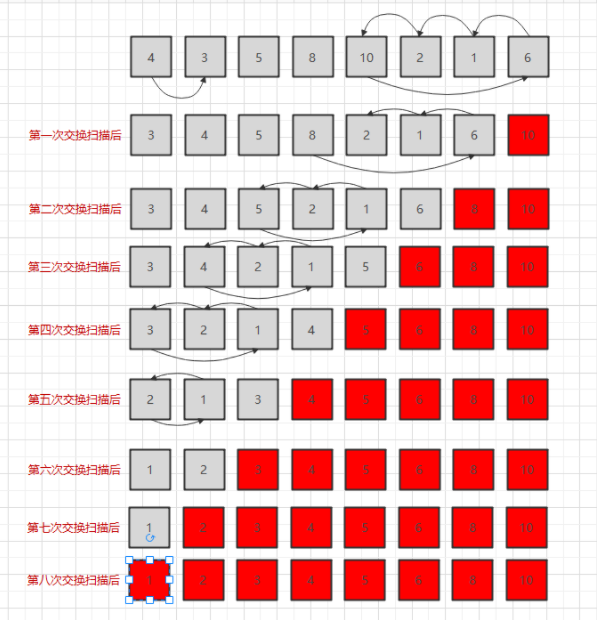
2.4、基本步骤

有一组n个元素的数据。
扫描交换：

1. 取出第1个元素与后面的元素比较
2. 如果后面的元素比较小，就将两个元素进行交换
3. 重复1-2步骤，从1元素到n-1个元素

冒泡排序：

1. 重复n-1次冒泡排序。

2.4、动态显示

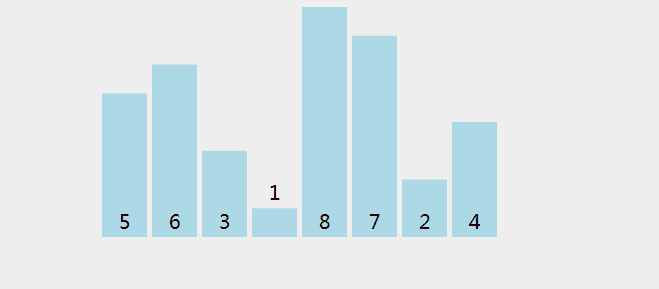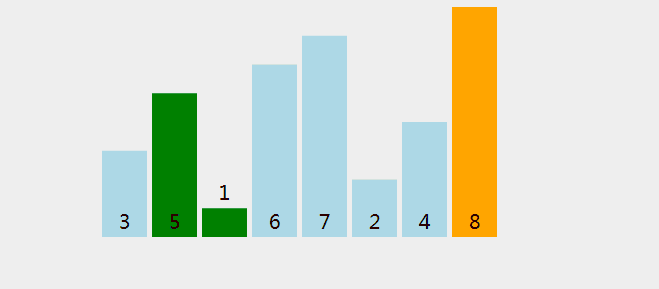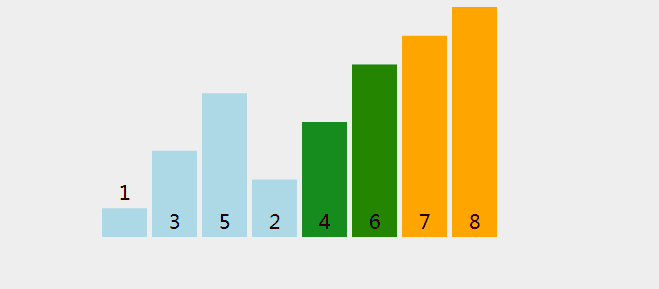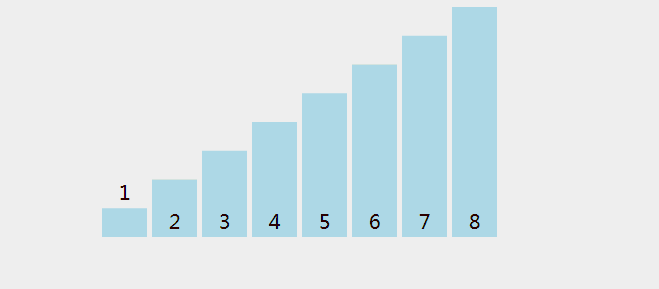
2.5、代码实现

    public static void sort(Integer[] arr) {
        // 进行n-1次扫描交换
        for (int i = 0; i < arr.length-1; i++) {
            // 扫描交换
            for (int j = 0; j < arr.length-1; j++) {
                // 获取当前元素的值
                int temp = arr[j];
                // 如果大于后面元素的值就交换
                if (temp > arr[j + 1]) {
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

2.6、优化代码

1. 由于扫描交换后会增加一个有序元素，所以在扫描交换的时候我们可以不再扫描已经有序了的元素。
2. 在基本的原理的图中我们可以发现，8个元素经过了6次扫描交换后即变成有序的数据了，不再需要扫描n-1次即7次，所以我们可以在扫描交换后判断数据中的元素是否有元素交换，如果没有交换即已经变成了有序的数据了就可以终结扫描。

优化后的代码

    public static void improveSort(Integer[] arr){
        // 用于判断是否已经有序的便利
        boolean isSort = true;
        // n-1次扫描交换
        for (int i = 0; i < arr.length-1; i++) {
            // 扫描交换，每次扫描后就不再扫描已经有序的元素。arr.length-i-1
            for (int j = 0; j < arr.length-i-1; j++) {
                // 获取当前元素的值
                int temp = arr[j];
                // 如果大于后面元素的值就交换
                if (temp > arr[j+1]){
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    // 如果有交换就表示数据不是有序的
                    isSort = false;
                }
            }
            // 判断数据是否有序，有序就终极扫描，排序完毕
            if (isSort){
                break;
            }else {
                isSort = true;
            }
        }
    }

测试优化

测试代码

    public static void main(String[] args) {
        // 从0-10000中获取10000个元素的数组
        Integer[] arr = SortUtils.getRandomArr(10000, 10000);
        long start1 = System.currentTimeMillis();
//        improveSort(arr);
        sort(arr);
        long end1 = System.currentTimeMillis();
        System.out.println("花费时间："+(end1-start1));
        SortUtils.printlnArr(arr);
    }

未优化的结果，大概500-600毫秒中间

优化后的结果，大概在340毫秒左右

2.7、时间复杂度

1. 最差情况

\[O（1+7*\sum_{i=1}^{n-1}n）=O（7*n*(n-1)/2）=O（7*n^2）=O（n^2） \]

2. 最好情况

\[O(1+7*(n-1))=O(n) \]

3. 平均情况(元素有一半的几率进行交换)

\[O（1+7*\sum_{i=1}^{(n-1)/2}n+4*\sum_{i=1}^{(n-1)/2}n）=O（n*(n-1)/2）=O（n^2）=O（n^2） \]

---

3、选择排序（selection sort）

3.1、什么是选择排序？

选择排序（Selection sort）是一种简单直观的排序算法。[3]

3.2、选择排序的基本思路

将序列划分为无序前缀和有序后缀两部分；此外，还要求前缀不大于后缀。如此，每次只需从前缀中选出最大者，并作为最小元素转移至后缀中，即可使有序部分的范围不断扩张，直到前缀消失，排序就完成了。
可以想象为打斗地主的时候理牌，从手中牌中抽出最大的一张放到最左边，依次对未理过的牌进行这样的操作，直到所有的牌都排序完毕。

3.3、基本步骤

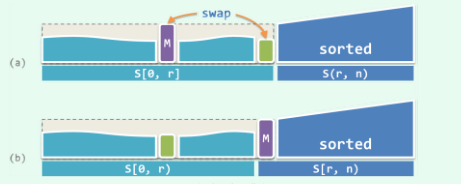
假设有个n个元素的数组，前缀是0-n 后缀为无

1. 从前缀中抽出第1个元素
2. 将其与前缀中所有的元素一一比较，如果小于前缀中的元素，就将其抽出继续比较。
3. 前缀比较完毕后将最后抽出来元素与后缀最后的一个元素的下一位交换位置。
4. 重复1-3知道前缀消失
   

3.4、实例

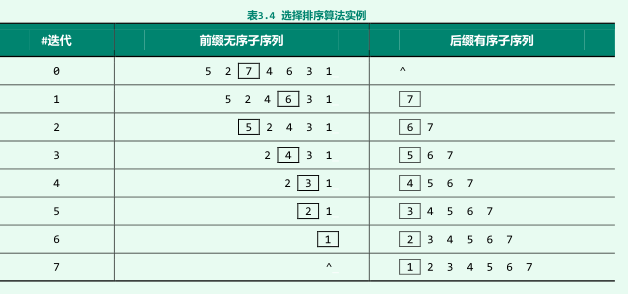
经过7此交换，数组已经变成了一个有序的数组，每次比较都会从前缀中抽取最大值与后缀最后一位的下一位前缀的位置交换，变成后缀的最后一位。

3.5、动态显示

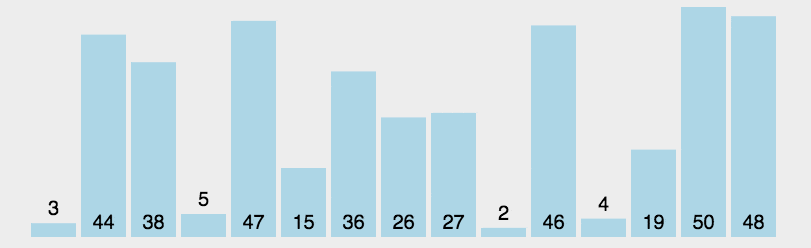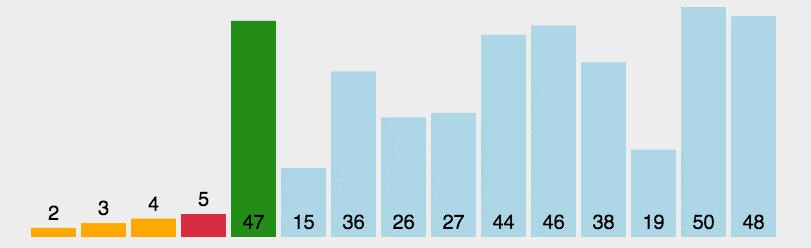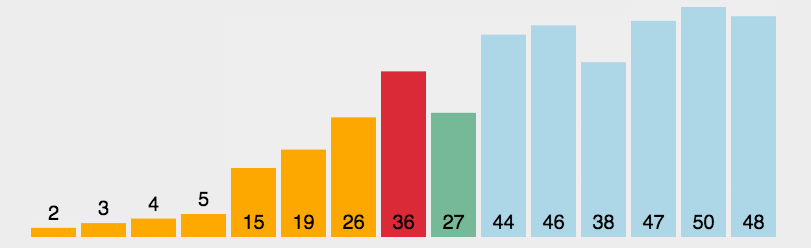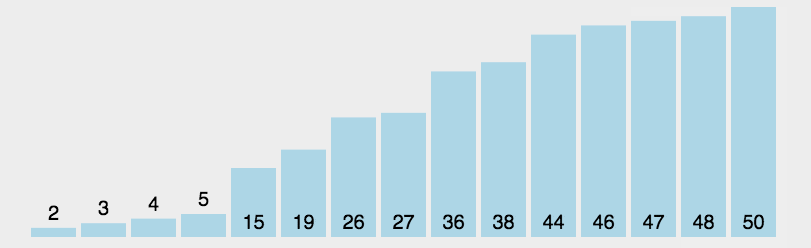
3.6、代码实现

    public static void simpleSelectSort(Integer[] arr){
        // 前缀中的最大值的索引
        Integer index;
        // 前缀中的最大值
        Integer max;
        // 进行n-1此找最大值交换
        for (int i = arr.length-1; i >= 0 ; i--) {
            // 将前缀获取临进后缀的元素的值和索引赋给max和 index
            max = arr[i];
            index = i;
            // 找出最大值
            for (int j = i; j >= 0; j--) {
                // 如果元素大于最大值就将值和索引都赋给max和index
                if (arr[j] > max){
                    max = arr[j];
                    index = j;
                }
            }
            // 如果没有值大过前缀获取临进后缀的元素
            if (i != index){
                // 与最大值进行交换
                exchange(arr, i,index);
            }
        }
    }

    public static void exchange(Integer[] arr,Integer index1,Integer index2){
        Integer temp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = temp;
    }

3.7、时间复杂度

为了节约时间，我们可以直接将与非循环的固定步骤变成O(1)

1. 最差情况

\[O(\sum_{1}^{n-1}n)=O(n^2) \]

1. 最好情况

\[O(\sum_{1}^{n-1}n)=O(n^2) \]

1. 平均情况

\[O(\sum_{1}^{n-1}n)=O(n^2) \]

4、简单插入排序（simple insert sort）

4.1、什么是简单插入排序

插入排序，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法[5]

4.2、简单插入排序的基本思路

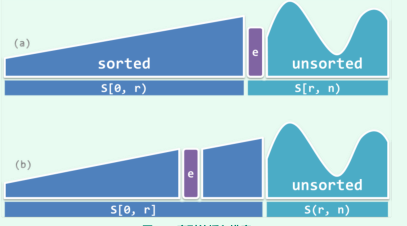
将序列划分为有序前缀和无序后缀两部分，将后缀中第一个元素移至前缀合适的位置保持前缀的有序性

4.3、基本步骤

有一个n个元素的数组，开始将[0,1）视为有序前缀，[1,n）视为无序后缀

1. 从左至右抽取后缀的第一个元素
2. 与前缀从右至左开始比较
   1. 如果抽取出来的后缀元素小于前缀元素就进行交换
   2. 如果大于，就停止
3. 重复1 2 直到后缀消失。
   
   

4.4、实例

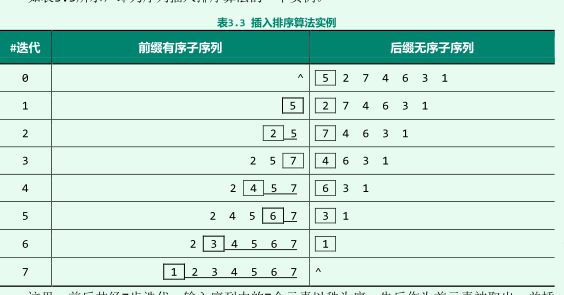
4.5、动态展示

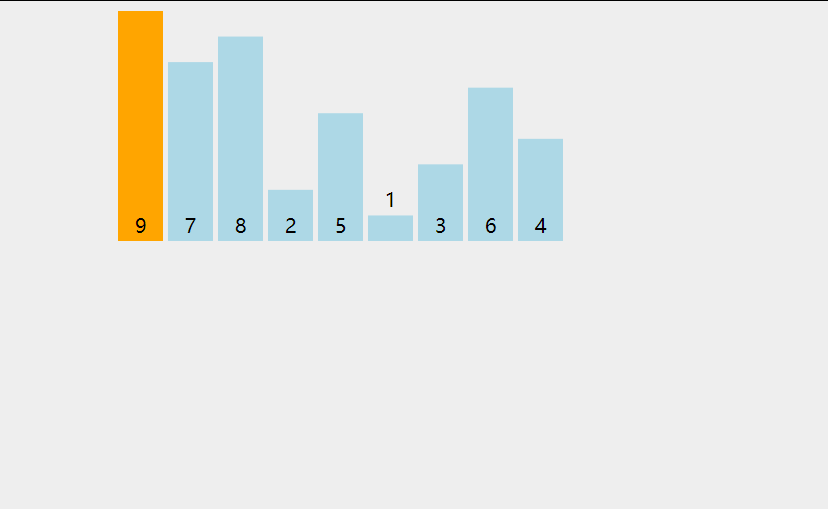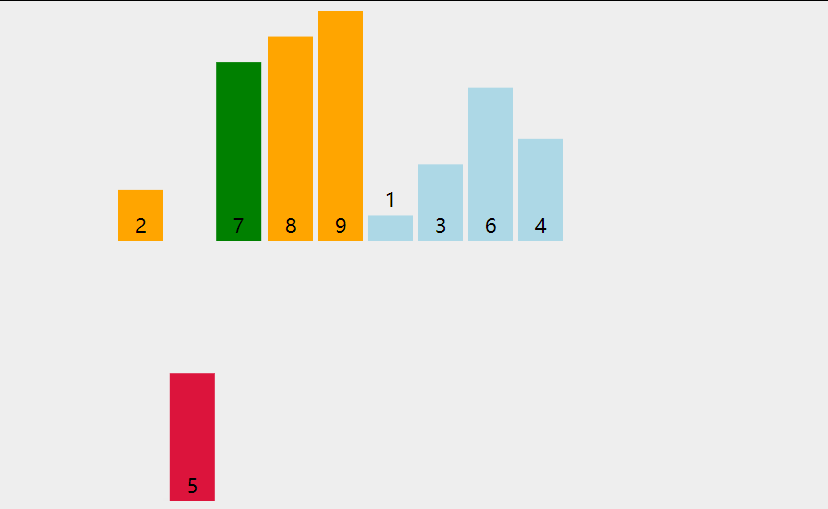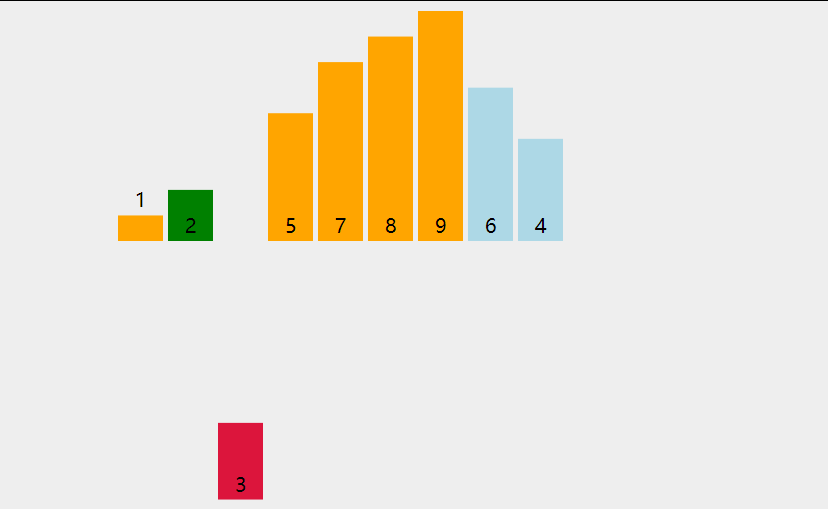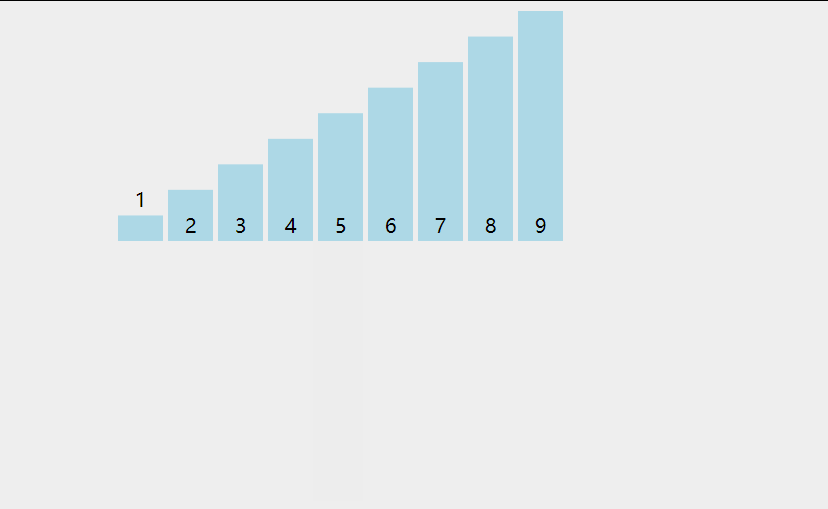
4.6、代码实现

移位法

    public static void moveSort(Integer[] arr){
        for (int i = 1; i < arr.length; i++) {
            // 抽去后缀中的第一个元素
            Integer temp = arr[i];
            // 从右至左依次与前缀比较
            for (int j = i-1; j >= 0; j--) {
                // 如果前缀元素大于temp就将其往后移移位
                if (temp < arr[j]){
                    arr[j+1] = arr[j];
                }else{
                    //否则就将temp赋给小于temp的前缀元素后面
                    arr[j+1] = temp;
                    break;
                }
                // 如果前缀中所有的元素都移位了，就直接将temp赋给第一个位置
                if (j == 0){
                    arr[j] = temp;
                    break;
                }
            }
        }
    }

交换法

    public static void swapSort(Integer[] arr){
        for (int i = 1; i < arr.length; i++) {
            // 从2个元素开始，从右至左与前一个元素开始比较
            for (int j = i; j > 0; j--) {
                // 如果小于前一个元素就进行交换
                if (arr[j] < arr[j-1]){
                    exchange(arr,j,j-1);
                }else{
                    break;
                }
            }
        }
    }
    public static void exchange(Integer[] arr,Integer index1,Integer index2){
        Integer temp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = temp;
    }

4.7、时间复杂度

最差情况

\[O(3*\sum_{1}^{n-1}n)=O(n^2) \]

平均情况

\[O(3*\sum_{1}^{n-1}n)=O(n^2) \]

最好情况

\[O(n) \]

5、总结

5.1、时间复杂度比较

排序算法	时间复杂度(最差)	时间复杂度(平均)	时间复杂度(最好)
冒泡排序	O(n^2)	O(n^2)	O(n)
简单插入排序	O(n^2)	O(n^2)	O(n)
选择排序	O(n^2)	O(n^2)	O(n^2)

虽然根据上面的公式我们可以轻易的看出来选择排序是最垃圾，冒泡排序和选择排序差不多。但是这些都只是理论上的数据，那么实际测试是怎样的呢？

测试代码

        // 从0-10000中获取10000个元素的数组
        Integer[] arr = SortUtils.getRandomArr(10000, 10000);
        long start1 = System.currentTimeMillis();
        improveSort(arr);
        long end1 = System.currentTimeMillis();
        System.out.println("花费时间："+(end1-start1));
        SortUtils.printlnArr(arr);

如果时10000个10000以内的随机数，那么多次的结果是

冒泡排序340毫秒左右

选择排序50毫秒以内

插入排序270毫秒左右

如果时100000个100000以内的随机数，那么多次的结果是

冒泡排序40000毫秒左右

选择排序6000毫秒左右

插入排序18000毫秒左右

如果时500000个500000以内的随机数，那么1次的结果是

冒泡排序1243428毫秒

选择排序330943毫秒

插入排序889498毫秒

思考

三个排序算法在实际的操作中有了明显区别，并不像理论的那样（我测试的本质是测试平均情况）。我们可以明显的发现选择排序是最好的，插入排序其次，冒泡排序最差。这是为什么呢？
个人看法：可能在冒泡排序和插入排序的时候右大量的交换操作，而交换操作就一定牵扯到写操作，写操作(赋值)比其他的操作比较费时，所以明显操作在减少但是由于右大量的写操作导致实际时间增加。当人操作时间其实跟很多因素都有关系，比如硬件的硬盘内存等，软件的操作系统，编程语言等有关系，所以我的这个测试是有一定的局限性。
但是无论如何，三个排序算法，都会随着数据量的增大，时间呈指数增加，这明显不是一个好的算法的表现。那么有没有更好一点的算法呢？答案是肯定的。