games 101 第三课作业

完整讲太累了，只挑重点讲

    objl::LoaderLoader;

  这次引入了一个新的第三方.obj 文件加载库来读取更加复杂的模型文件，这部分库文件在 OBJ_Loader.h file. 我们无需详细理解它的工作原理，只需知道这个库将会传递给我们一个被命名被 TriangleList 的 Vector，其中每个三角形都有对应的点法向量与纹理坐标。此外，与模型相关的纹理也将被一同加载。

  不过为了了解读取的三角形法向量和纹理坐标的格式还是去要去看看类定义如：

        std::vector<Vertex> Vertices;以Vertex为对象的数组。

 在Vertices中依次存放着每个三角形的每个顶点的相关数据

struct Vertex
{
    Vector3 Position;// 顶点坐标
    Vector3 Normal;// 顶点法向量
    Vector2 TextureCoordinate;// 纹理映射的uv坐标
};

创建三角形逐个读取mesh中存储的三角形信息

for(int i=0;i<mesh.Vertices.size();i+=3)//i计数每次加3，是因为要从每个三角形的第一个顶点开始逐个读入
{
    Triangle* t = new Triangle();//创建三角形
    for(int j=0;j<3;j++)//通过i+j依次读取每个三角形的数据,同时j也标志着三角形内部顶点的顺序，安装逆时针方向
    {
        t->setVertex(j,Vector4f(mesh.Vertices[i+j].Position.X,mesh.Vertices[i+j].Position.Y,mesh.Vertices[i+j].Position.Z,1.0));//设置齐次坐标的去空间点坐标
        t->setNormal(j,Vector3f(mesh.Vertices[i+j].Normal.X,mesh.Vertices[i+j].Normal.Y,mesh.Vertices[i+j].Normal.Z));//设置三角形顶点法向量
        t->setTexCoord(j,Vector2f(mesh.Vertices[i+j].TextureCoordinate.X, mesh.Vertices[i+j].TextureCoordinate.Y));//设置uv坐标
    }
    TriangleList.push_back(t);//把三角形插入一个存储三角形用的向量组
}

之后就是读取贴图 ：

autotexture_path = "hmap.jpg";

r.set_texture(Texture(obj_path+texture_path));

Texture 的输入是纹理的路径，通过cv：：read 函数读取该路径指定的纹理图片，并依据该纹理的的分辨率设置长宽。

再通过set_texture() 函数将该纹理设置到光栅器当中。

接下来这行代码重点理解一下：

    std::function<Eigen::Vector3f(fragment_shader_payload)> active_shader = phong_fragment_shader;

  先理解一下std::function,是一个函数包装模板，std::function对象可被拷贝和转移，并且可以使用指定的调用特征来直接调用目标元素。

这行代码将phong_fragment_shader包装为active_shader,且函数的输入数据格式为fragment_shader_payload,输出数据格式为Eigent：：Vector3f

  关于Eigen::Vector3f phong_fragment_shader函数的之后再说，因为关系到作业。

  从这里开始先完成我们的作业：

实现法向量、颜色、纹理颜色的插值

  要完成rasterize_triangle(newtri, viewspace_pos);  首先要看调用它的rst::rasterizer::draw函数。

  对每个三角形计算他们经过mvp变换中的mv变换之后的顶点坐标，这是因为为了实习纹理映射需要计算机顶点的法向量，但是mv矩阵的变换可能导致原先的法向量与切向量不再垂直，因此要在mv变换之后再求一次法向量。不再完整的mvp矩阵之后做的原因是：p变换是为了实现变换到相机空间的变换，此时的坐标都是为了方便进行正交投影的变换后的坐标。并非在“真实”的世界坐标系下，没有必要在这个坐标系下求顶点的法向量，在这个坐标系下求法向量反而会影响实际的着色。

Triangle newtri = *t;
        std::array<Eigen::Vector4f, 3> mm {
                (view * model * t->v[0]),
                (view * model * t->v[1]),
                (view * model * t->v[2])
        };
        std::array<Eigen::Vector3f, 3> viewspace_pos;
        std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
            return v.template head<3>();
        });
        Eigen::Vector4f v[] = {
                mvp * t->v[0],
                mvp * t->v[1],
                mvp * t->v[2]
        };
        //Homogeneous division
        for (auto& vec : v) {
            vec.x()/=vec.w();
            vec.y()/=vec.w();
            vec.z()/=vec.w();//这里需要注意一个点，还并未对坐标进行完整的齐次化，因为需要w保存z坐标
        }

下面是求经过mp变换后的法向量的代码：

Eigen::Matrix4f inv_trans = (view * model).inverse().transpose();
Eigen::Vector4f n[] = {
    inv_trans * to_vec4(t->normal[0], 0.0f),
    inv_trans * to_vec4(t->normal[1], 0.0f),
    inv_trans * to_vec4(t->normal[2], 0.0f)
    };

  然后调用rasterize_triangle(newtri, viewspace_pos); 传入了三角形顶点上的各种属性（法线，颜色等），以及三角形在view_space的顶点坐标。只所以传入顶点坐标是为了在后续对各种属性做出正确的插值，这个步骤是此次作业的坑点之一。

  先来看代码我认为是错误版本的代码：

void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos) 
{   
    auto v = t.toVector4();
    float ymin=std::min(std::min(v[0][1],v[1][1]),v[2][1]);float ymax=std::max(std::max(v[0][1],v[1][1]),v[2][1]);
    float xmin=std::min(std::min(v[0][0],v[1][0]),v[2][0]);float xmax=std::max(std::max(v[0][0],v[1][0]),v[2][0]);
    for(int x=xmin;x<=xmax;x++){
        for(int y=ymin;y<=ymax;y++){
            if(insideTriangle(x+0.5,y+0.5,t.v)){
                auto[alpha, beta, gamma] = computeBarycentric2D(x+0.5 , y+0.5 , t.v);
                float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float Z = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                float zp=Z * w_reciprocal;

                if(zp>depth_buf[get_index(x,y)]){
                        auto interpolated_color=interpolate(alpha,beta,gamma,t.color[0],t.color[1],t.color[2],1);
                        auto interpolated_normal =interpolate(alpha,beta,gamma,t.normal[0],t.normal[1],t.normal[2],1);
                        auto interpolated_texcoord =interpolate(alpha,beta,gamma,t.tex_coords[0],t.tex_coords[1],t.tex_coords[2],1);
                        auto interpolated_shadingcoords=interpolate(alpha,beta,gamma,view_pos[0],view_pos[1],view_pos[2],1);
                        Use: fragment_shader_payload payload( interpolated_color, interpolated_normal.normalized(), interpolated_texcoord, texture ? &*texture : nullptr);
                        payload.view_pos = interpolated_shadingcoords;
                        auto pixel_color = fragment_shader(payload);
                        set_pixel(Eigen::Vector2i(x,y),pixel_color);
                        depth_buf[get_index(x,y)] = zp;
                }
            }
        }
    }

  这个代码的前部分和我们以前在作业1、2中完成的代码一样先是求出屏幕空间中bounding box然后遍历其中的所有像素，再运行函数insideTriangle（） 判断像素中点是否在三角形中。之后便是之前在作业1、2中掠过的部分透视矫正插值。

   透视矫正插值

  

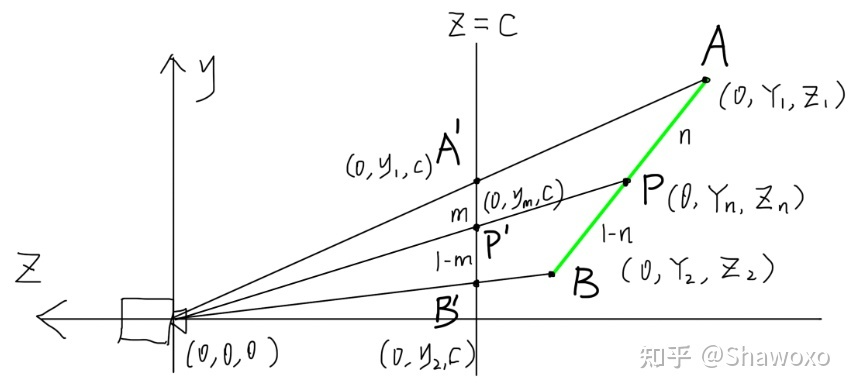
  方便起见以深度Z的线性插值为例，虽然图片是2维的但是可以假设AB为未经投影变换的一条空间中的垂直X轴的直线，image plane的线条本身与y轴平行，camera的观察方向与z轴平行。

  然后假设c点由a、b点插值所得 c = a + s ∗ ( b − a ) ，连接视点和c的直线和AB相交于C点(Xt​,Zt​)，显然C点投影到z=d上得到c点。现在已知 A,B点的Z坐标Z1​,Z2​，以及c点的插值系数s，需要找到一个表达式求出C点的Z坐标Zt​。

  首先要分别过A点和过B点做2条平行于A'B'的直线，相交于C'C及其延长线，构成相似三角形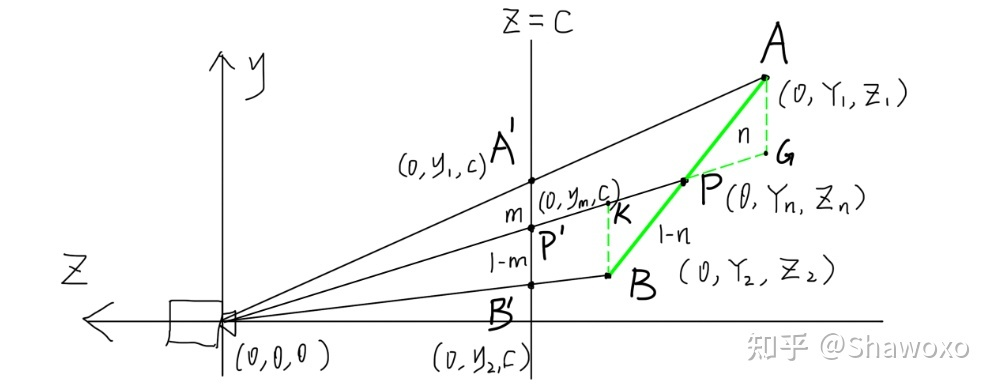

  则由相似可得：

 

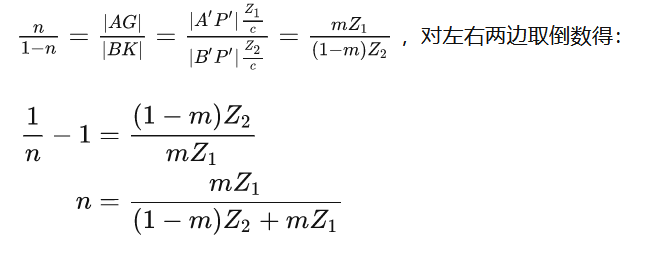
  到现在，我们就可以根据m和世界坐标求出n了，而 P=(1-n)A+nB ，于是我们现在可以对其进行任何插值计算了，只需替换A和B为相应的属性即可。比如P点的z坐标应该为：

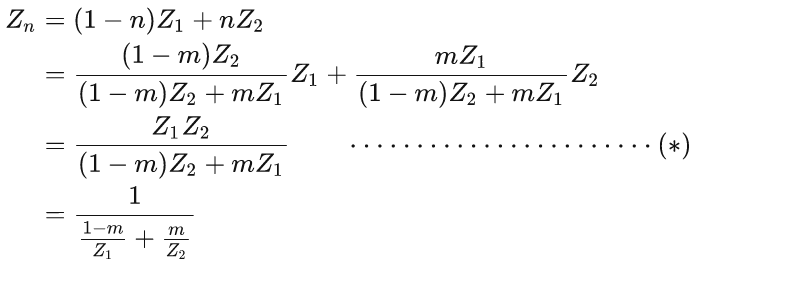
  可以将1-m和m分别用α和β替换，且α+β=1；