games101作业1以及框架理解

main.cpp

头文件与常量

#include <iostream>
#include <opencv2/opencv.hpp>
#include "rasterizer.hpp"
#include "global.hpp"
#include "Triangle.hpp"
constexpr double MY_PI = 3.1415926;

代码开头引入了一堆头文件，并不是很重要，其中global.hpp、Triangle.hpp与rasterize.hpp是我们自定义的。

MY_PI是我们自定义的圆周率常量，使用constexpr。这里有个点是constexpr与const的差别：const强调只读，constexpr强调常量（点击此处做更多了解）。常量表达式(const expression）是指值不会改变并且在编译过程就能得到计算结果的表达式。而const可以通过 const type & 应用来改变其值。不过在该处影响不大。

main()函数

int main(int argc, const char** argv)

这句话中argc是命令行总的参数个数,argv则是数组字符串。argc不用显式的输入而是会自动统计，而在以0为开始下标argv的字符串数组中则储存了所有参数，一般第0个参数是程序的全名。具体用法如下：Rasterzier是第0个参数是程序全名，-r是第1个参数意为当前的模式，20是第2个参数为旋转的度数，image.png是第3个参数为存储的图片名。

./Rasterizer //循环运行程序，创建一个窗口显示，且你可以
//使用A键和D键旋转三角形。
./Rasterizer −r 20 //运行程序并将三角形旋转20度，
//然 后 将 结 果 存 在output.png中
 ./Rasterizer −r 20 image.png //运行程序并将三角形旋转20度，
//然 后 将 结 果 存 在image.png中。

然后是一系列初始化：

    rst::rasterizerr(700, 700);          //初始化700*700的光栅化器，实际是将frame_buf与depth_buf初始化为该尺寸的向量。
    Eigen::Vector3feye_pos = {0, 0, 5};  //定义摄像机坐标，其数据类型为Eigen库的三维数组。
    std::vector<Eigen::Vector3f> pos{{2, 0, -2}, {0, 2, -2}, {-2, 0, -2}}  //定义pos数组，该数组中每个对象的数据类型都为
    //eigen库的三维浮点数组。
    std::vector<Eigen::Vector3i> ind{{0, 1, 2}};    //定义顶点顺序

初始化完成后相光栅器中传入pos与ind：

    autopos_id = r.load_positions(pos);
    autoind_id = r.load_indices(ind);

load_positions()是rasterizer内部的函数：

rst::pos_buf_id rst::rasterizer::load_positions(const std::vector<Eigen::Vector3f> &positions){
    auto id = get_next_id();
    pos_buf.emplace(id, positions);
    return {id};
}

int get_next_id() { return next_id++; }

rasterizer的类中定义了 next_id的值，其初始值为0；每传入一组pos都会使返会当前next_id的值给id，并使next_id的值加1。而pos_buf的数据类型是std::map<int,std::vector<Eigen::Vector3f>>，使用map.emplce（）函数向pos_buf中写入该数据。pos_buf的每对数据中id都是不同的。最后load_postions函数再将当前传入的坐标的id返回。load_indices也是相同的思路，对应的pos数组与ind数组的id是相同的。

然后初始化：

    intkey = 0;          //捕捉键盘输入字符的ASCII码
    intframe_count = 0;  //帧计数

接下来的这段代码我们可以先略过，因为这是在使用命令行启动程序并在一定条件下才会生效的语句，对我们理解图像生成的过程意义不大。

    if (command_line) {
        r.clear(rst::Buffers::Color|rst::Buffers::Depth);

        r.set_model(get_model_matrix(angle));
        r.set_view(get_view_matrix(eye_pos));
        r.set_projection(get_projection_matrix(45, 1, 0.1, 50));

        r.draw(pos_id, ind_id, rst::Primitive::Triangle);
        cv::Matimage(700, 700, CV_32FC3, r.frame_buffer().data());
        image.convertTo(image, CV_8UC3, 1.0f);

        cv::imwrite(filename, image);

        return0;
    }

直接看：

    while (key != 27) {　　
        r.clear(rst::Buffers::Color|rst::Buffers::Depth);

        r.set_model(get_model_matrix(angle));
        r.set_view(get_view_matrix(eye_pos));
        r.set_projection(get_projection_matrix(45, 1, 0.1, 50));

        r.draw(pos_id, ind_id, rst::Primitive::Triangle);

        cv::Matimage(700, 700, CV_32FC3, r.frame_buffer().data());
        image.convertTo(image, CV_8UC3, 1.0f);
        cv::imshow("image", image);
        key = cv::waitKey(10);

        std::cout<<"frame count: "<<frame_count++ <<'\n';

        if (key == 'a') {
            angle += 10;
        }
        elseif (key == 'd') {
            angle -= 10;
        }
    }

这一段代码是生成图像的过程，首先key用于捕捉我们键盘的输入。Key=27对应的是在键盘上按下'ESC'键，按下'ESC'后结束while循环并退出程序。

然后看r.clear,clear也是rasterizer内部定义的函数。rst::Buffers::Color 与 rst::Buffers::Depth都内部定义的枚举类：

enum class Buffers{
    Color = 1,
    Depth = 2
};

而rst::Buffers::Color | rst::Buffers::Depth之间的'|'的运算符也有经过重写：

inline Buffers operator|(Buffers a, Buffers b){  
    return Buffers((int)a | (int)b);
}

重写'|'操作符是返回经过int数据类型转换后的枚举类的值的|操作即按位或运算。

(int) rst::Buffers::Color=1 其二进制为01

(int) rst::Buffers::Depth=2 其二进制为10

(int) (rst::Buffers::Color | rst::Buffers::Depth)=3 其二进制为11

结合clear（）函数的定义：

void rst::rasterizer::clear(rst::Buffers buff)
{
    if ((buff & rst::Buffers::Color) == rst::Buffers::Color)
    {
        std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{0, 0, 0});
    }
    if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth)
    {
        std::fill(depth_buf.begin(), depth_buf.end(), std::numeric_limits<float>::infinity());
    }
}

clear()将输入rst::Buffers buff分别与rst::Buffers::Color和rst::Buffers::Depth进行同位与操作，若rst::Buffers buff与rst::Buffers::Color的同位与操作与rst::Buffers::Color 相等则将frame_buf中的所有向量都以Eigen::Vector3f数据类型的{0, 0, 0}替换，若rst::Buffers buff与rst::Buffers::Depth的同为与操作与rst::Buffers::Depth 相等这将depth_buf中的所有向量都以

std::numeric_limits<float>::infinity() 替换。

然后讨论

        r.set_model(get_model_matrix(angle));
        r.set_view(get_view_matrix(eye_pos));
        r.set_projection(get_projection_matrix(45, 1, 0.1, 50));

分别调用了三个函数，将光栅器r内部的model,view与projection赋值：

void rst::rasterizer::set_model(const Eigen::Matrix4f& m){
    model = m;
}
void rst::rasterizer::set_view(const Eigen::Matrix4f& v){
    view = v;
}
void rst::rasterizer::set_projection(const Eigen::Matrix4f& p){
    projection = p;
}

关于get_model_matrix(angle)，get_view_matrix(eye_pos)和get_projection_matrix(45, 1, 0.1, 50)的讨论放在下面的Model-View-Projection矩阵变换的定义中讨论。

Model-View-Projection矩阵的定义

首先明确MVP矩阵的作用：

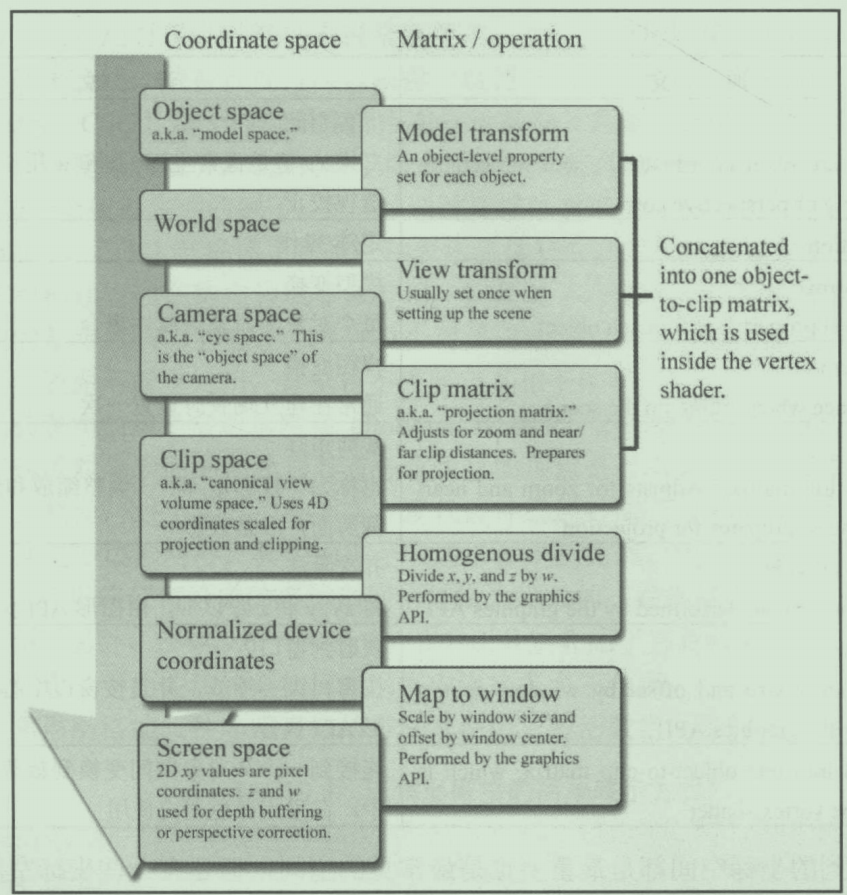
Model transform

可以看到通过Model transform，从对象空间（Object space）转换到了世界空间（World space）。在课堂中老师讲到Model transformation的作用是Find a good place and arrange people ，其实其作用就是通过旋转和位移矩阵从对象空间转移到直立空间再到世界空间。

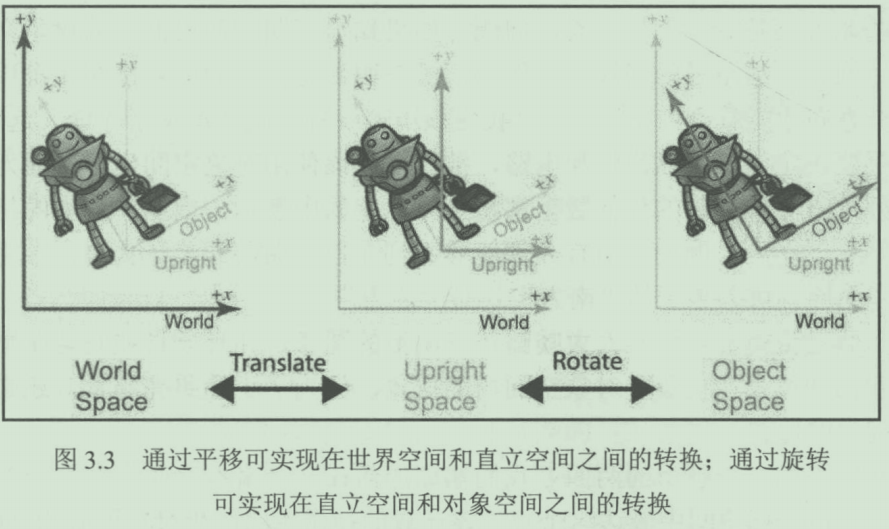
那么Model就是通过先旋转后位移的的方式转移到世界坐标。

回到games101的作业中讨论该问题：

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    return model;
}

作业1中要求我们补充该函数：但是目的是绕z轴旋转。已经由上面描述，图像通过旋转，位移从对象空间到直立空间再到世界空间。但是给到的作业中并没有涉及到位移矩阵，我的理解是默认对象空间的原点与世界空间的原点重合，同时程序默认世界空间的轴经过rotation_angle的角度的正方向旋转后与对象空间的轴重合。从对象空间变换到世界空间意味着使用对象空间中的点的坐标乘以描述对象空间轴在世界空间中方向的矩阵，以世界坐标系描述所有点。如果将点在对象空间中的坐标和点在世界空间中的坐标都直接表现在世界空间中的话，前者也确实是后者正向旋转rotation_angle的角度以后的结果。

因此经过补充的代码如下所示

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    rotation_angle = rotation_angle / 180 * MY_PI;
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f rotation;
    rotation<<std::cos(rotation_angle),-std::sin(rotation_angle),0,0,
              std::sin(rotation_angle),std::cos(rotation_angle),0,0,
              0,0,1,0,
              0,0,0,1;
    model =rotation*model;
    return model;
}

View transform

View transform和Model Transform很类似，Model Transform是将对象空间转换到世界空间，而View Transform则是从世界空间转换到相机空间。

先决定相机摆放的位置（将相机移动到原点），再决定相机的gaze directon即相机朝哪看，最后决定相机的向上方向up-direction（相机本身的以gaze-direction方向为轴的旋转）。

不过通常我们会有关于相机约定俗成的一些规定，如永远在原点，gaze-direction朝-Z方向，up-direction与+Y同方向。

然后我们要解决的问题是将摄像机摆放的原点以我们约定的朝向。

将摄像机摆放到原点很简单只要通过以下矩阵：

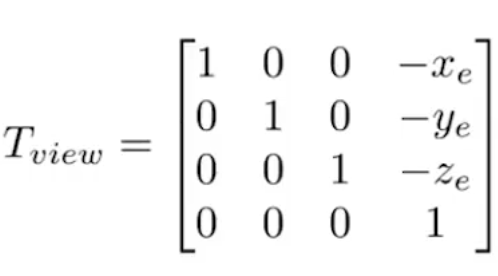
比较巧妙的是旋转，描述摄像机朝向的矩阵可以通过以下矩阵描述

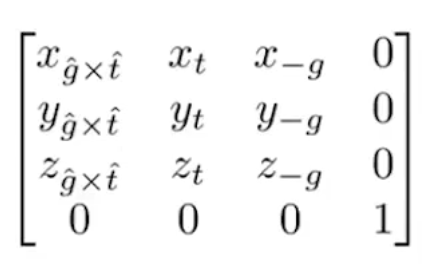
t轴对应的up-direction，g则对应gaze-direction。因为要使所有轴经过旋转能与坐标轴重合且相机空间的轴的正方向与世界空间的正方向相同，而g指向世界空间的-Z，所以相机空间的Z轴要用-g来描述，是相机空间的Z轴与世界空间的Z轴同方向。而相机空间的X轴通过g叉乘t得出。我们可以通过该矩阵的逆矩阵使相机空间的所有轴和世界空间所有的轴对齐，因为该矩阵是正交矩阵，所以该矩阵的逆矩阵为其转置。

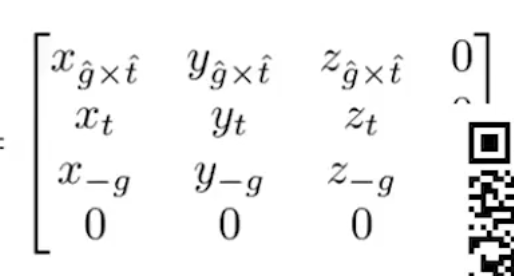
代码中默认所有轴均已对齐，暂时只需要将相机移动到原点。

Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos){
    Eigen::Matrix4f view = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f translate;
    translate << 1, 0, 0, -eye_pos[0],
                 0, 1, 0, -eye_pos[1], 
                 0, 0, 1,-eye_pos[2],
                 0, 0, 0, 1;
    view = translate * view;
    return view;
}

Projection Transform

在进行投影变换之前，需要了解透视投影(Perspective projection)和正交投影（Orthographic projection）.

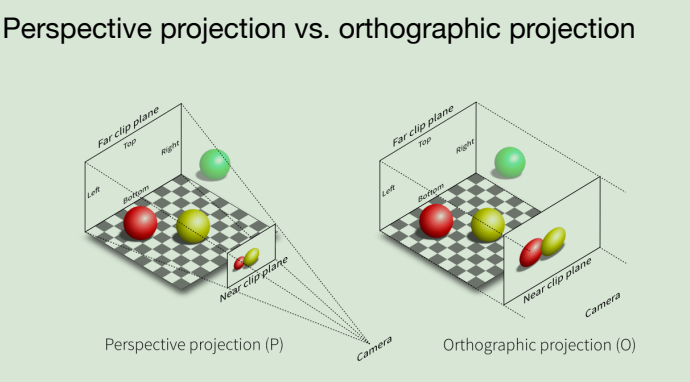
正交投影变换用一个长方体来取景，并把场景投影到这个长方体的前面。这个投影不会有透视收缩效果（远些的物体在图像平面上要小一些），因为它保证平行线在变换后仍然保持平行，也就使得物体之间的相对距离在变换后保持不变。简单的说，正交投影变换忽略物体远近时的大小缩放变化，将物体以原比例投影到截面（如显示屏幕）上，实现这样效果的照相机叫做正交投影照相机，也称正交照相机。

透视投影变换跟正交投影一样，也是把一个空间体（指的是以投影中心为顶点的透视四棱锥）投影到一个二维图像平面上。然而，它却有透视收缩效果：远些的物体在图像平面上的投影比近处相同大小的物体的投影要小一些。跟正交投影不同的是，透视投影并不保持距离和角度的相对大小不变，所以平行线的投影并不一定是平行的了。
处理正交投影的过程是将一个盒形的视锥体移动，使其中点和原点重合，再将该视锥体变形成[-1,1]³ 的立方体。

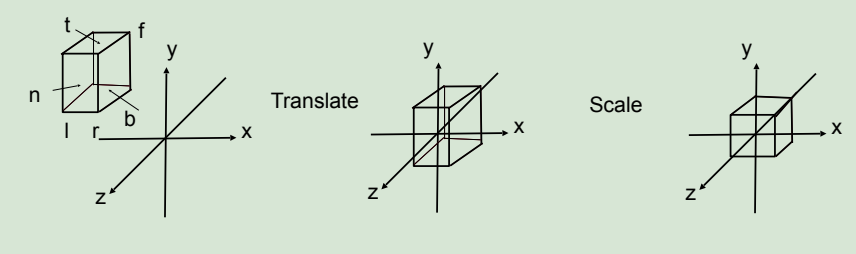
ln general
- We want to map a cuboid [l,r]x [b,t]x [f, n] to
the "canonical (正则、规范、标准)”cube [-1,1]³

正交投影的正交矩阵如下所示，我们的程序默认左乘，所以是先位移变换再做比例的变换。

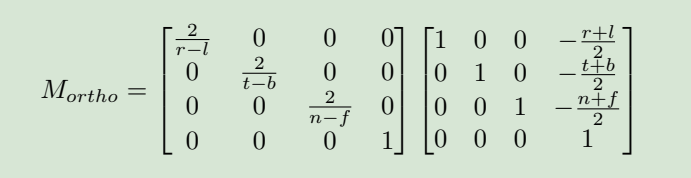
^{透视投影的不同则是先将视锥体挤压成盒形，再做正交投影。}

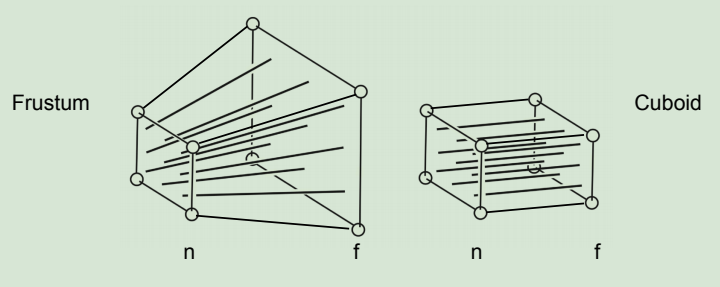
^{具体的代码如下所示。}

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar){
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f persp;
    Eigen::Matrix4f translate;
    Eigen::Matrix4f scale;
    eye_fov=(eye_fov/180.0)*MY_PI;
    float n=abs(zNear);
    float f=abs(zFar);
    float t=n*tanf(eye_fov/2);
    float r=aspect_ratio*t;
    persp    <<zNear,0,0,0,
               0,zNear,0,0,
               0,0,zFar+zNear,-zFar*zNear,
               0,0,1,0;
    translate<<1,0,0,0,
               0,1,0,0,
               0,0,1,-(zFar+zNear)/2,
               0,0,0,1;
     scale   <<1/r,0,0,0,
               0,1/t,0,0,
               0,0,2/(f-n),0,
               0,0,0,1;
    projection=scale*translate*persp;
    return projection;
}

posted @ 2022-08-20 20:39 ahab1016 阅读(89) 评论(0) 收藏举报

刷新页面返回顶部

ahab1016