求三角形面积

 

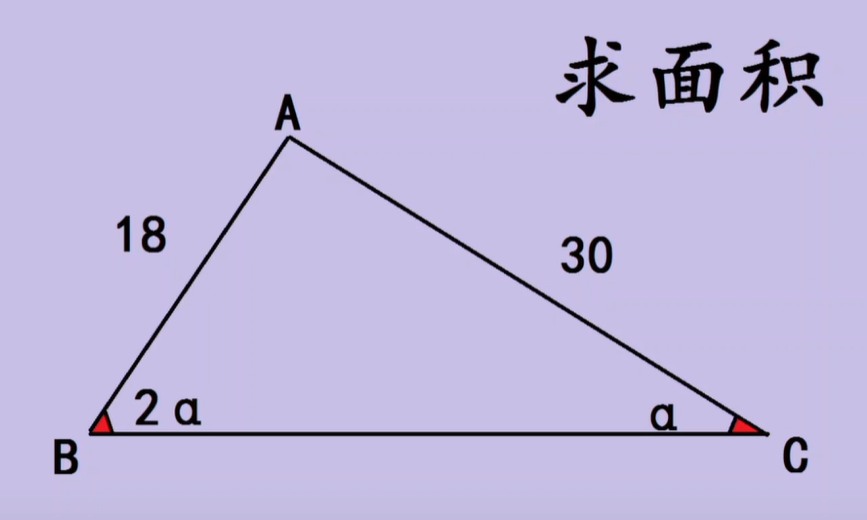
设$BC$之高为$h$，$h$与$BC$的交点为$H$。

 

根据正弦函数，可知

      $\sin\alpha=\frac{h}{AC}=\frac{h}{30}$

      $\sin2\alpha=\frac{h}{AB}=\frac{h}{18}$
      $h=18\sin2\alpha=30\sin\alpha$

∵    $\sin2\alpha=2\sin\alpha\cos\alpha$

∴    $\frac{h}{18}=2·\frac{h}{30}·\cos\alpha$

∴    $\cos\alpha=\frac{5}{6}$

 

∵    $\sin^2+\cos^2=1$

∴    $\sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-{\frac{5}{6}}^2 }= \sqrt{\frac{11}{36}}=\frac{\sqrt{11}}{6}$

∴    $h= 30\sin\alpha=30·\frac{\sqrt{11}}{6} = 5\sqrt{11}$

∴    $\sin2\alpha=\frac{h}{18}=\frac{5\sqrt{11}}{18}$

∴    $\cos2\alpha=\sqrt{1-sin^2 2\alpha}=\sqrt{1-{\frac{5 \sqrt{11}}{18}}^2}=\frac{7}{18}$
可得：

      $BH=AB\cos2\alpha=18\times\frac{7}{18}=7$

      $HC=AC\cos\alpha=30\times\frac{5}{6}=25$

      $BC=BH+HC=7+25=32$

 

∴    三角形面积

      $S=\frac{BC\times h}{2}=\frac{32\times5\sqrt{11}}{2}=80\sqrt{11}$

 

使用到的数学知识：

1. 三角函数
2. 三角函数公式
   1. 平方关系公式
   2. 二倍角公式
3. 平方根乘除运算
4. 三角形面积公式