广度优先遍历

概述

广度优先搜索的设计思想

广度优先搜索以顶点 u 为起始点，依次访问和 u 有路径相通且路径长度为 1、2、…的顶点。

广度优先搜索的基本思想是

• 访问顶点 u，然后依次访问 u 的各个未被访问的邻接点 v1、v2、…、vk，
• 分别从 v1、v2、…、vk 出 发依次访问它们未被访问的邻接点
• 至图中所有与顶点 u 有路径相通的顶点都被访问到

为了使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问，设置队列存储已被访问的顶点

算法：BFS
输入：起始顶点 u
输出：搜索经过的顶点序列
       1. 队列 Q 初始化;
       2. 访问顶点 u; 修改标志visited[u]=1; 顶点 u 入队列 Q;
       3. 当队列 Q 非空时执行下述操作：
            3.1 u = 队列 Q 的队头元素出队;
            3.2 v =顶点 u 的邻接点；
            3.3 重复下述操作直至 v 不存在： 
                  3.3.1 如果 v 未被访问，则
                           访问顶点 v; 修改标志visited[v]=1; 顶点 v 入队列 Q；
                  3.3.2 v =顶点 u 的下一个邻接点；

例题

农夫抓牛

假设农夫和牛都位于数轴上，农夫位于点 \(N\)，牛位于点 \(K（K>N）\)，农夫有以下两种移动方式

• 从点 \(X\) 移动到 \(X-1\) 或 \(X+1\)，每次移动花费一分钟
• 从点 \(X\) 移动到点 \(2X\)，每次移动花费一分钟

假设牛没有意识到农夫的行动，站在原地不动，农夫最少要花费多长时间才能抓住牛？

分析

将数轴上每个点看作是图的顶点，对于任意点 \(X\)，有两条双向边连到点 \(X-1\) 和 \(X+1\)，有一条单向边连到点 \(2X\)，则农夫抓牛问题转化为求从顶点 N 出发到顶点 K 的最短路径长度

如图，假设 N=3，K=5，广度优先搜索过程如右图所示，最短路径长度是 2

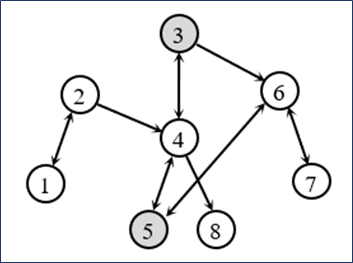
实现

int catchCattle(int N,int K){
	int flag[K]={0};
	int Q[K]={0};
	//队列遍历指针
	int front=-1,rear=-1;
	
	//初始化
	Q[++rear]=N;
	flag[N]=1;
	int u,v;
	int step=0;
	//right指针指向队列最后一个元素
	int right=0;
	while(front!=rear){
		u=Q[++front];
		if(u==K){
			return step;
		}
		v=u-1;
		if(flag[v]==0){
			Q[++rear]=v;
			flag[v]=1;
		}
		v=u+1;
		if(flag[v]==0){
			Q[++rear]=v;
			flag[v]=1;
		}
		v=u*2;
		if(flag[v]==0){
			Q[++rear]=v;
			flag[v]=1;
		}
		if(front==right){
			step++;
			right=rear;
		}
	}
	return -1;
}

骑士旅行

题目

国际象棋的骑士走“日”字并且可以越子，在一个国际象棋的棋盘上，给定起点\((x_1, y_1)\)和终点\((x_2, y_2)\)，计算骑士从起点到终点最少需要移动的步数

分析

骑士每次移动的位置增量有八个方向。骑士旅行问题属于寻找最短路径问题，可以用广度优先搜索求解

实现

struct status{
	int x;
	int y;
	int step;
};
int x[8]={-2,-1,1,2,2,1,-1,-2};
int y[8]={1,2,2,1,-1,-2,-2,-1};


int kingnightBFS(status s,status t){
	int flag[8][8]={0};
	status u,v,next,Q[64];
	int front=-1,rear=-1;

	Q[++rear]=s;
	flag[s.x][s.y]=1;

	while(front!=rear){
		u=Q[++front];
		if(u.x==t.x&&u.y==t.y)
			return u.step;
		for(int i=0;i<8;i++){
			next.x=u.x+x[i];
			if(next.x<0||next.x>7)
				continue;
			next.y=u.y+y[i];
			if(next.y<0||next.y>7)
				continue;
			if(flag[next.x][next.y]==0){
				next.step=u.step+1;
				Q[++rear]=next;
				flag[next.x][next.y]=1;
			}
	}
	return -1;

}

A*算法

A*算法是一种启发式搜索算法，用于在有向图中找到从起点到终点的最短路径

所谓启发式搜索是通过启发式函数引导算法的搜索方向，以达到减少搜索结点的目的

启发式函数通常利用与问题有关的某种启发信息，对于路径搜索问题，结点就是搜索空间的状态，启发信息通常是距离，启发式函数表示为：

\[f(n) = g(n) + h(n) \]

其中，

• \(f(n)\)是从初始状态到目标状态的估计代价；
• \(g(n)\)是从初始状态到状态n的实际代价；
• \(h(n)\)是从状态n到目标状态最佳路径的估计代价

A*算法以优先队列形式组织的open表，存储搜索过程中经过的状态，每次从open表中选取 f(n) 值最小（或最大）的结点作为下一个待扩展的结点

算法：A*算法
输入：问题模型，启发式函数
输出：最优值
       1. 将起始状态加入open表中；
       2. 重复下述操作直到open表为空：
           2.1 n = open表中第一个状态结点；
           2.2 如果结点 n 为终点，则返回最优值，算法结束；
           2.3 结点 n 不是终点，执行下述操作：
                 2.3.1 将结点 n 从open表中删除；
                 2.3.2 生成结点 n 的所有子结点：
                 2.3.3 计算所有子结点的估价函数值；
                 2.3.4 将所有子结点加入open表中，并按估价函数排序；
       3. 搜索失败；

A*算法能够尽快找到或最优解的关键在于函数h(n)的选取,以d(n)表示状态n到目标状态的最短距离，则h(n)的选取大致有如下三种情况

• \(h(n) < d(n)\)，搜索的结点数较多，搜索范围较大，效率较低，但能保证得到最优解。h(n)值越小，搜索越多的结点，也就导致算法效率越低。
• h(n) = d(n)，搜索将严格沿着最短路径进行，此时的搜索效率最高。在没有达到终点之前，很难确切计算出距离终点还有多远。
• h(n) > d(n)，搜索的结点数较少，搜索范围较小，效率较高，但不能保证得到最优解。因为启发仅仅是下一步将要采取措施的一个猜想，这个猜想常常根据经验和直觉来判断，所以启发式搜索可能出错。

八数码问题

问题

八数码问题也称重排九宫问题，在一个 3×3 的方格盘上，放有 1~8 个数码，余下一格为空，空格四周上下左右的数码可以移动到空格。给定一个八数码问题的初始状态，要求找到一个移动序列到达目标状态

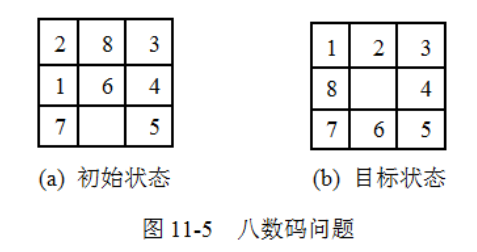
应用 A*算法求解八数码问题的关键是确定启发式函数，可以将实际代价函数g(n)定义为解空间树中从根结点到该状态的路径长度（即移动次数），估计代价函数h(n)定义为该状态与目标状态不相符的数码个数

多段图的最短路径问题

问题

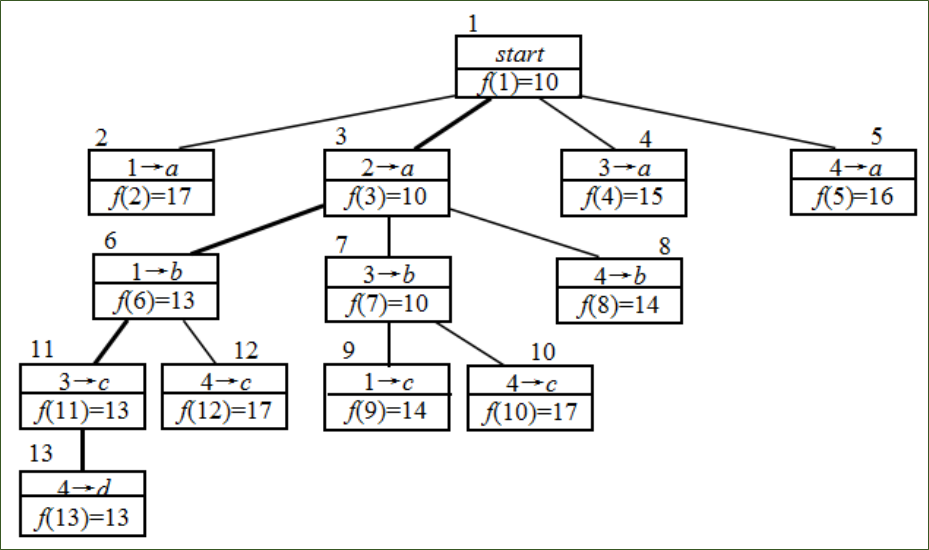
设\(G=(V, E)\)是一个带权有向连通图，如果把顶点集合 V 划分成k个互不相交的子集 \(V_i（2≤k≤n, 1≤i≤k）\)，使得 \(E\) 中的任一条边\((u, v)\)，必有 \(u∈Vi，v∈Vi+m（1≤i＜k, 1＜i+m≤k）\)，称 \(s∈V1\) 为源点，\(t∈Vk\) 为终点。
多段图的最短路径问题是求从源点到终点的最小代价路径

分析

设可以将g(i)定义为从源点到顶点 i 的实际路径长度，将h(i)定义为从顶点 i 到终点每一段的最小代价之和
启发函数为：

\[g(i)=\sum_{j=1}^{j}c[r_{j-1}][r_j]\\ h(i)=\min_{r_j}c[r_{i}][r_p]+\sum_{j=i+2}^{k}第j段的最小代价 \]

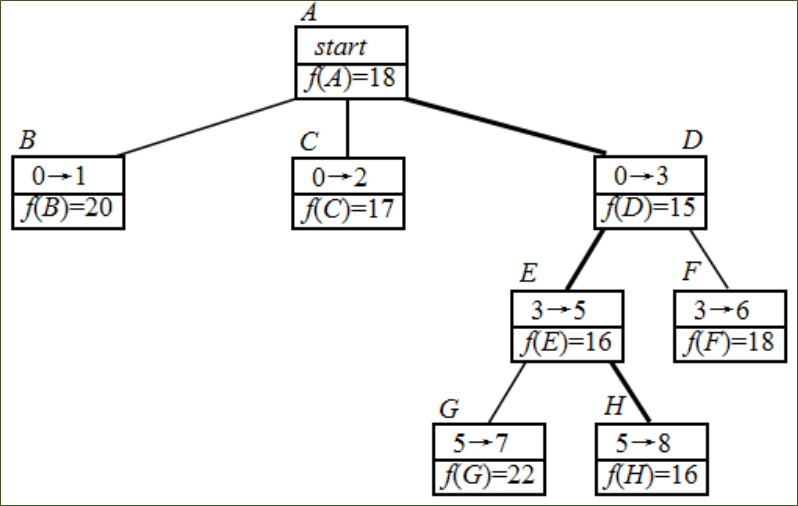
任务分配问题

问题

把 n 项任务分配给 n 个人，每个人完成每项任务的成本不同，任务分配问题要求总成本最小的最优分配方案

分析

将g(n)定义为已经分配的任务成本，h(n)定义为其余任务的最小分配成本。任务分配问题可以采用成本矩阵表示，令 cij 表示人员i分配了任务 j（1≤i, j≤n），一般情况下，假设当前已对人员 1～i 分配了任务，启发式函数定义如下

\[g(n)=\sum_{k=1}^{i}c_{Kx_k}\\ h(n)=\sum_{k=i+1}^{n}第k行的最小值 \]

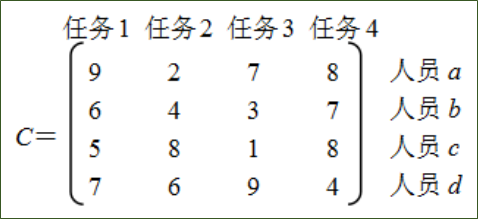
限界剪枝法

限界的设计思想

限界剪枝法首先确定一个合理的限界函数，并根据限界函数确定目标函数的界[down, up]。然后，按照广度优先策略搜索问题的解空间树
在分支结点上，依次扩展该结点的所有孩子结点，分别估算这些孩子结点的目标函数值，如果某孩子结点的目标函数值超出目标函数的界，则将其丢弃，因为从这个结点生成的解不会比目前已经得到的解更好；否则，将其加入open表中。依次从open表中选取使目标函数取得极值的结点成为当前扩展结点，重复上述过程，直至找到最优解

因为限界函数常常基于问题的目标函数而确定，所以，限界剪枝法适用于求解最优化问题

实质上，限界剪枝法是在A*算法的基础上加入剪枝操作，减少open表中的结点数量，从而提高搜索效率

算法：限界剪枝法
输入：问题模型，限界函数
输出：最优值
       1. 根据限界函数确定目标函数的界[down, up]；
       2. 估算根结点的目标函数值并加入open表；
       3. 循环直到某个叶子结点的目标函数值在open表中取得极值：
           3.1 n = open表中具有极值的结点；
           3.2 对结点 n 的所有子结点 x 执行下述操作：
                 3.2.1 估算结点 x 的目标函数值value;
                 3.2.2 若value在[down, up]中，则将结点 x 加入open表；否则丢弃结点 x；
       4. 输出叶子结点对应的最优值，回溯求得最优解的各个分量；

关键问题

• 确定合适的限界函数
  好的限界函数要求
  • 计算简单；
  • 保证最优解在搜索空间中；
  • 能在搜索的早期对超出目标函数界的结点进行丢弃，减少搜索空间，从而尽快找到问题的最优解。
• open表的存储结构
  为了能快速在open表中选取使目标函数取得极值的结点，通常采用优先队列存储open表。如果open表的结点数不是很多，也可以简单的采用数组存储
• 确定最优解的各个分量
  限界剪枝法跳跃式处理搜索空间中的结点，需要对每个扩展结点保存该结点到根结点的路径，或者在搜索过程中构建搜索经过的树结构。

0/1背包问题

分析

假设 n 种物品已按单位价值由大到小排序，可以采用贪心法求解 0/1背包问题的一个下界。
如背包中装入的全部是第 1 个物品且可以将背包装满，则可以得到一个上界非常简单的计算方法： \(ub=C×(v_1/w_1)\)

例如：
4 个物品重量为(4, 7, 5, 3)，价值分别为(40, 42, 25, 12)，背包容量 C=10。

贪心法求得的下界为：\(lb=40+25=65\)
若背包中装入的全部是第 1 个物品且可以将背包装满，则可以得到一个上界：\(ub=10×(40/4)=100\)

则本问题的限界范围为：\([65, 100]\)

TSP问题

分析

考虑TSP问题的一个完整解，路径上每个城市都有两条邻接边，一条是进入这个城市的，另一条是离开这个城市的，那么，把矩阵中每一行最小的两个元素相加再除以 2，就得到了一个合理的下界

这个下界对应的解可能不是一个可行解（没有构成哈密顿回路），但给出了一个参考下界。

圆的排列问题

问题

给定 n 个圆的半径序列，将这些圆放到一个矩形框中，各圆与矩形框的底边相切，则圆的不同排列会得到不同的排列长度。要求找出具有最小长度的圆排列。

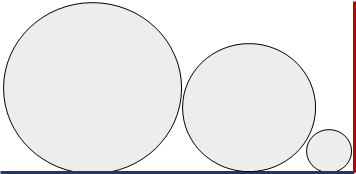
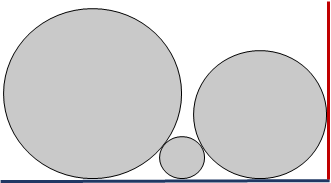
不同的排列方式会造成长度不同

分析

定义

• \(x_k\)：第 k 个位置所放圆的圆心坐标，规定第 1 个圆的圆心为坐标原点，即 x1=0。
• \(d_k\)：第 k 个位置所放圆的圆心坐标与第 k-1 个位置所放圆的圆心坐标的差。
• \(L_k\)：第 1~k 个位置放置圆后，可能得到的目标函数的极小值

有

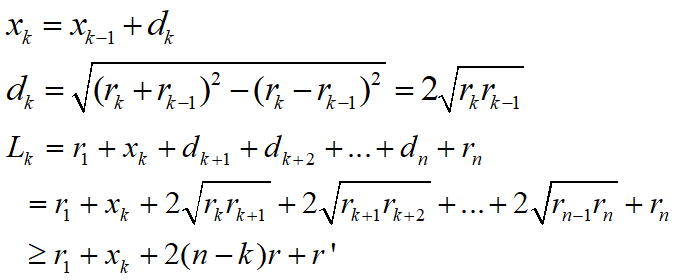
批作业处理问题

分析

• 上界：可以随机产生几个调度方案，从中选取具有最短完成时间的调度方案作为近似最优解
• 下界：

电线布线问题

题目

印刷电路板将布线区域划分成n×m个方格如图a所示。精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案。在布线时，电路只能沿直线或直角布线，如图b所示。为了避免线路相交，已布了线的方格做了封锁标记，其它线路不允穿过被封锁的方格

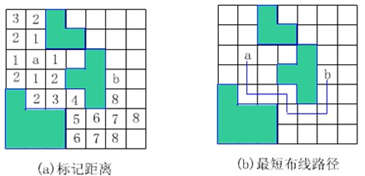
分析

从起始位置a开始将它作为第一个扩展结点。与该扩展结点相邻并且可达的方格成为可行结点被加入到活结点队列中，并且将这些方格标记为1，即从起始方格a到这些方格的距离为1。

接着，算法从活结点队列中取出队首结点作为下一个扩展结点，并将与当前扩展结点相邻且未标记过的方格标记为2，并存入活结点队列。这个过程一直继续到算法搜索到目标方格b或活结点队列为空时为止