贪心法
概述
贪心法把一个复杂问题分解为一系列较为简单的局部最优选择,每一步选择都是对当前解的一个扩展,直至获得问题的完整解。
求解过程
应用贪心法的关键是确定贪心选择策略,这种贪心策略只是根据当前信息作出最好的选择,不去考虑在后面看来这种选择是否合理
贪心法即使不能得到整体最优解,通常也是最优解的很好近似
例题
付款问题
问题
假设有面值为 5元、2元、1元、5 角、2 角、1 角的货币,需要找给顾客4 元 6 角现金,付款问题要求找到一个付款方案,使得付出的货币张数最少
分析
贪心选择策略:每次都找面值最大的货币,直到找不出更大的面值为止
值得注意的是,不一定能找出最优解,比如找给顾客 4 元 6 角,贪心法会找出 5 元、1 元、1 角、1 角、1 角,但是最优解是 2 元、2 元、1 角、1 角
实现
int payMoney(double sum){
int money[6]={50, 20, 10, 5, 2, 1};
int count=0,n=sum*10;
int i=0;
while(n>0){
if(n>=money[i]*10){
n-=money[i]*10;
count++;
}
else
i++;
}
}
TSP问题
问题
给定一个有 n 个城市的地图,每个城市之间都有一条道路相连,求从某个城市出发,经过每个城市一次,最后回到出发城市的最短路径
分析
从任意城市出发,每次在没有到过的城市中选择最近的一个,直至经过了所有城市,最后回到出发城市
实现
int TSP(int *arc[],int n,int w){
bool flag[n]={false};
int edgeCount=0;
int TSPLength=0;
int u=w;
flag[u]=true;
while(edgeCount<n-1){
int min=9999;
int v;
for(int i=0;i<n;i++){
if(arc[u][i]<min && flag[i]==false){
min=arc[u][i];
v=i;
}
}
TSPLength+=arc[u][v];
cout<<u<<"->"<<v<<endl;
u=v;
flag[u]=true;
edgeCount++;
}
cout<<u<<"->"<<w<<endl;
TSPLength+=arc[u][w];
return TSPLength;
}
图着色问题
问题
求无向连通图G=(V, E)的最小色数 k,使得用 k 种颜色对 G 中的顶点着色,可使任意两个相邻顶点着不同颜色
分析
贪心法解决着色问题
- 选择一个颜色,依次对所有自身未着色且邻接点未着色的顶点进行着色
- 选择下一个颜色,依次对所有自身未着色且邻接点着色不冲突的顶点进行着色
- 依次进行,直至所有顶点都被着色
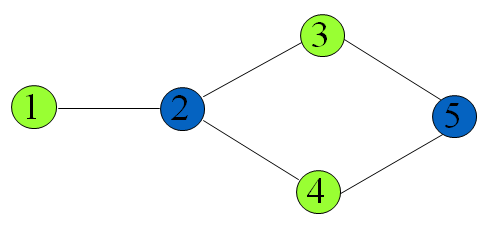
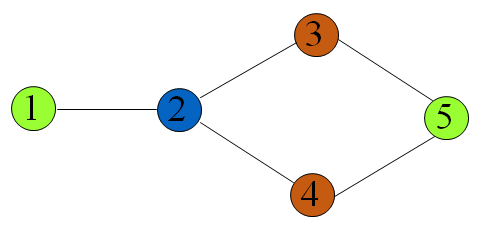
这种贪心策略是不一定能得到最优解的,比如对于下图,贪考虑顶点顺序为1、2、3、4、5得到最优解
考虑顶点顺序为1、5、2、3、4得到近似解
实现
int colorGraph(int *arc[],int n,int color[]){
int m=n;
int k=0;
while(m>0){
k++;
for(int i=0;i<n;i++){
if(color[i]!=0)
continue;
//找到第一个没有着色的点,着新色
color[i]=k;
m--;
//找到所有与它相邻的点,跳过着色
int j;
for(j=0;j<n;j++){
if(arc[i][j]==1&&color[j]==k)
break;
}
if(j==n)
continue;
//如果有相邻的点着了新色,那么这个点就不能着新色,跳过
else{
color[i]=0;
m++;
}
}
}
return k;
}
最小生成树
问题
给定一个连通图,求生成树中边的权值之和最小的生成树
分析
贪心法求解最小生成树:prim算法
- 从图中任意选取一个顶点作为初始顶点,将其加入到生成树中
- 找到与初始顶点相邻的最小权值的边,将该边的另一个顶点加入到生成树中
- 循环寻找与生成树相邻的最小权值的边,将该边的另一个顶点加入到生成树中
实现
int prim(int *r[],int n,int w){
int lowcost[n];
int closest[n];
int minDist=0;
for(int i=0;i<n;i++){
lowcost[i]=r[w][i];
closest[i]=w;
}
lowcost[w]=0;
int m=n-1;
while(m--){
int k;
int min=999;
for(int i=0;i<n;i++){
if(lowcost[i]<min&&lowcost[i]!=0){
min=lowcost[i];
k=i;
}
}
cout<<"k="<<k<<endl;
//k点放入树中
minDist+=lowcost[k];
lowcost[k]=0;
cout<<closest[k]<<"---"<<k<<endl;
//更新lowcost和closest
for(int i=0;i<n;i++){
if(lowcost[i]!=0&&r[k][i]<lowcost[i]){
lowcost[i]=r[k][i];
closest[i]=k;
}
}
}
return minDist;
}
背包问题
问题
给定 n 个物品和一个容量为 C 的背包,物品\((i1 ≤ i ≤ n)\)的重量是 \(w_i\),其价值为 \(v_i\),背包问题是如何选择装入背包的物品,使得装入背包中物品的总价值最大
分析
选择单位重量价值最大的物品(与0/1背包问题不同,背包内物品可以切分)
实现
double knapSack(int w[],int v[],int n,int C){
double x[n]={0};
int maxV=0;
int i=0;
for(i=0;w[i]<=C;i++){
x[i]=1;
maxV+=v[i];
C-=w[i];
}
if(C>0){
x[i]=(double)C/w[i];
maxV+=v[i]*x[i];
}
return maxV;
}
活动安排问题
问题
设有 \(n\) 个活动的集合 \(E=\{1, 2, …, n\}\),其中每个活动都要求使用同一资源,而在同一时间只有一个活动能使用这个资源。每个活动 \(i(1 ≤ i ≤ n)\)都有一个要求使用该资源的起始时间 \(s_i\) 和一个结束时间 \(f_i\),且 \(s_i < f_i\) 。如果选择了活动\(i\),则它在半开时间区间\([s_i, f_i )\)内占用资源。若区间\([s_i, f_i )\)与区间\([s_j, f_j )\)不相交,则称活动 \(i\) 与活动 \(j\) 是相容的。
活动安排问题要求在所给的活动集合中选出个数最多的相容活动
分析
贪心法求解活动安排问题
- 最早开始时间:增大活动利用率
- 最早结束时间:使下一个活动尽早开始
后者更合适,因为活动安排问题的目标是使得活动的总数最大,而不是使得活动的总时间最长,贪心策略为选择最早结束的活动
实现
int activityManage(int s[],int f[],int B[],int n){
//设s[]和f[]已经按照f[]的非递减顺序排列
int count=0;
B[0]=0;
count++;
int k=0;
for(int i=1;i<n;i++){
if(s[i]>=f[k]){
B[count]=i;
count++;
k=i;
}
}
return count;
}
埃及分数
问题
古埃及人只用分子为 1 的分数,在表示一个真分数时,将其分解为若干个埃及分数之和,例如:7/8 表示为 1/2 + 1/3 + 1/24。埃及分数问题要求把一个真分数表示为最少的埃及分数之和的形式
分析
贪心法求解埃及分数问题:
选择小于此真分数的最大埃及分数
实现
int egyptFraction(int a,int b){
while(a!=1){
int c=b/a+1;
cout<<1<<"/"<<c<<" + ";
a=a*c-b;
b=b*c;
//通分
for(int i=2;i<=a;i++){
if(a%i==0&&b%i==0){
a=a/i;
b=b/i;
}
}
}
cout<<1<<"/"<<b<<endl;
}
田忌赛马
问题
田忌和齐王赛马,他们各有 n 匹马,每次双方各派出一匹马进行赛跑,获胜的一方记 1 分,失败的一方记 -1 分,平局不计分,假设每匹马只能出场一次,每匹马有个速度值,比赛中速度快的马一定会获胜。田忌知道所有马的速度值,且田忌可以安排每轮赛跑双方出场的马,问田忌如何安排马的出场次序,使得最后获胜的比分最大?
分析
- 田忌最快的马比齐王最快的马快,则直接记1分
- 田忌最快的马比齐王最快的马慢,则用田忌最慢的马比齐王最快的马,记-1分
- 田忌最快的马和齐王最快的马速度相同
- 田忌最慢的马比齐王最慢的马快,则直接记1分(齐王最慢的马肯定会输,则消耗最差的和他比)
- 田忌最慢的马比齐王最慢的马慢,则用田忌最慢的马比齐王最快的马,记-1分
实现
int TianjiHorse(int t[],int q[],int n){
int s=0;
int t1=0,q1=0,t2=n-1,q2=n-1;
while(t1<=t2){
//1
if(t[t1]>q[q1]){
s++;
t1++;
q1++;
}
//2
else if(t[t1]<q[q1]){
s--;
t2--;
q1++;
}
//3
else{
//3.1
if(t[t2]>q[q2]){
s++;
t2--;
q2--;
}
//3.2
else if(t[t2]<q[q2]){
s--;
t1++;
q2--;
}
}
}
return s;
}
哈夫曼算法
问题
给出各元素权重,生成哈夫曼树,计算最小带权路径长度
分析
利用贪心算法,每次选择权重最小的两个元素,生成一个新的元素,权重为两个元素权重之和,重复此过程,直到所有元素都被合并为一个元素
实现
int huffman(int w[],int n){
int s=0;
while(n>1){
int min1=0,min2=1;
if(w[min1]>w[min2]){
int temp=min1;
min1=min2;
min2=temp;
}
for(int i=2;i<n;i++){
if(w[i]<w[min1]){
min2=min1;
min1=i;
}
else if(w[i]<w[min2]){
min2=i;
}
}
s+=w[min1]+w[min2];
w[min1]=w[min1]+w[min2];
w[min2]=w[n-1];
n--;
}
return s;
}
练习
-
- 题目:对于给定n位正整数a,删掉其中任意的k位数字,使得剩下的数字按原次序组成的新整数仍然是一个正整数,且新整数尽可能小。例如,当n=5,k=2,a=32547时,应输出247
- 分析:贪心法,从高位开始,如果当前位比后一位大,则删除当前位,否则不删除,直到删除k位
- 实现:
void deleteK(int a[],int n,int k){ int i=0; while(k>0){ if(a[i]>a[i+1]){ for(int j=i;j<n-1;j++){ a[j]=a[j+1]; } k--; if(i>0){ i--; } } else{ i++; } } for(int i=0;i<n-k;i++){ cout<<a[i]; } } ``` -
- 题目:有n个顾客,顾客\(i\)需要的时间为\(t_i\),如何安排这n个顾客的服务顺序,使得所有顾客的等待时间之和最小?
- 分析:贪心法,每次选择等待时间最短的顾客
- 实现:
void customer(int t[],int n){ int s=0; for(int i=0;i<n;i++){ int min=i; for(int j=i+1;j<n;j++){ if(t[j]<t[min]){ min=j; } } int temp=t[i]; t[i]=t[min]; t[min]=temp; s+=t[i]*(n-i-1); } cout<<s<<endl; } -
- 问题:一辆汽车加满油后可以行驶m公里,途中有若干加油站,距离由A[m]给出,其中A[i]表示第i-1个加油站到i加油站的距离,起点终点各有一个加油站,计算加油最少次数
- 分析:贪心法,每次选择能到达的最远的加油站
- 实现:
int car(int a[],int n,int m){ int i=0; //加满 int last=n; int sum=0; for(i=0;i<m;i++){ last=last-a[i]; if (last<0) break; if(a[i]>last){ sum++; last=n; } } if(i==m) return sum; else return -1; } -
- 问题:TSP采用最短链接策略,每次选择最短的边加入解集合,保证最终形成哈密顿回路,设计算法求解TSP问题
- 分析:首先按照城市之间距离远近进行排列,从距离最近的两个城市开始,如果这两个城市不在一个联通分量中并且度数均小于等于2,那么记录二者之间的路径,将它们划分到一个联通分量并将度数增加1;然后从距离第二小的两个城市开始,重复上述操作直到记录的路径有n-1条,最后找到度数为1的两个城市,作为最后一条路径。
- 实现:
//最短链接策略TSP问题 int tsp(int **a,int n){ //保存连接图中每个点的度 int d[n]={0}; int k=n; int totalLenth=0; while(k>0){ //找到权重最小的边 int min=10000; int minI,minJ; for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ if(a[i][j]<min&&a[i][j]!=0){ min=a[i][j]; minI=i; minJ=j; } } } //如果这条边的两个顶点的度都小于2,则加入到最短路径中 if(d[minI]<2&&d[minJ]<2){ totalLenth+=a[minI][minJ]; d[minI]++; d[minJ]++; a[minI][minJ]=0; cout<<minI<<"->"<<minJ<<endl; k--; } else a[minI][minJ]=10000; } return totalLenth; } -
- 问题:Kruskal算法生成最小生成树
- 分析:首先将所有边按照权重从小到大排序,然后从权重最小的边开始,如果这条边的两个顶点不在一个联通分量中,那么将这条边加入到最小生成树中,否则不加入,直到最小生成树中有n-1条边为止
- 实现:
//Kruskal算法生成最小生成树 int kruskal(int **a,int n){ int totalLenth=0; int k=n; while(k>0){ //找到权重最小的边 int min=10000; int minI,minJ; for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ if(a[i][j]<min&&a[i][j]!=0){ min=a[i][j]; minI=i; minJ=j; } } } //如果这条边的两个顶点不在一个联通分量中,那么将这条边加入到最小生成树中 if(!isConnected(a,minI,minJ,n)){ totalLenth+=a[minI][minJ]; a[minI][minJ]=0; cout<<minI<<"->"<<minJ<<endl; k--; } else a[minI][minJ]=10000; } return totalLenth; } -
- 问题:Dijkstra算法求解最短路径
- 分析:首先将所有顶点的距离初始化为无穷大,然后将起点的距离初始化为0,然后从起点开始,找到与起点相连的所有顶点,更新这些顶点的距离,然后从这些顶点中找到距离最小的顶点,重复上述操作直到所有顶点的距离都被更新
- 实现:
//Dijkstra算法求解最短路径 void dijkstra(int **a,int n,int start){ int *d=new int[n]; int *p=new int[n]; int *s=new int[n]; for(int i=0;i<n;i++){ d[i]=10000; p[i]=-1; s[i]=0; } d[start]=0; s[start]=1; for(int i=0;i<n;i++){ if(a[start][i]!=0&&a[start][i]!=10000){ d[i]=a[start][i]; p[i]=start; } } for(int i=0;i<n;i++){ int min=10000; int minI; for(int j=0;j<n;j++){ if(d[j]<min&&s[j]==0){ min=d[j]; minI=j; } } s[minI]=1; for(int j=0;j<n;j++){ if(a[minI][j]!=0&&a[minI][j]!=10000&&s[j]==0){ if(d[j]>d[minI]+a[minI][j]){ d[j]=d[minI]+a[minI][j]; p[j]=minI; } } } } for(int i=0;i<n;i++){ cout<<d[i]<<" "; } cout<<endl; for(int i=0;i<n;i++){ cout<<p[i]<<" "; } cout<<endl; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号