分治法
概述
分治法将一个难以直接解决的大问题划分成一些规模较小的子问题,分别求解各个子问题,再合并子问题的解得到原问题的解
求解过程
- 划分
把规模为 n 的原问题划分为 k 个(通常 k = 2)规模较小的子问题 - 求解子问题
分别求解各个子问题 - 合并
把各个子问题的解合并起来
启发式原则
- 平衡子问题
子问题的规模最好大致相同 - 各子问题之间相互独立
例题
汉诺塔问题
题目:
有一座宝塔(塔A)上有 64 个金碟,所有碟子按从大到小的次序从塔底堆放至塔顶。紧挨着这座宝塔有另外两个宝塔(塔 B 和塔 C),要求把塔 A 上的碟子移动到塔 C 上去,其间借助于塔 B 的帮助。每次只能移动一个碟子,任何时候都不能把一个碟子放在比它小的碟子上面
分析:
对于 n 个碟子的汉诺塔问题,其操作步骤如下:
- 将塔 A 上的 n-1 个碟子借助塔 C 先移到塔 B 上
- 把塔 A 上剩下的一个碟子移到塔 C 上;
- 将 n-1 个碟子从塔 B 借助塔 A 移到塔 C 上
实现:
void Hanio(int n, char a, char b, char c){
if(n==1){
cout<<a<<"-->"<<c<<endl;
}
else{
Hanio(n-1,a,c,b);
cout<<a<<"-->"<<c<<endl;
Hanio(n-1,b,a,c);
}
}
归并排序
分析:
- 划分
将待排序序列从中间位置划分为两个长度相等的子序列; - 求解子问题
分别对这两个子序列进行排序,得到两个有序子序列; - 合并
将这两个有序子序列合并成一个有序序列
实现
void Merge(int r[],int s,int m,int t){
int temp[t+1];
int i=s,j=m+1,k=s;
while(i<=m&&j<=t){
if (r[i]<=r[j])
temp[k++]=r[i++];
else
temp[k++]=r[j++];
}
while (i<=m){
temp[k++]=r[i++];
}
while (j<=t){
temp[k++]=r[j++];
}
for ( i = s; i <= t; i++){
r[i]=temp[i];
}
}
void mergeSort(int r[],int s,int t){
if(s==t) return;
else{
int m=(s+t)/2;
mergeSort(r,s,m);
mergeSort(r,m+1,t);
Merge(r,s,m,t);
}
}
快速排序
分析:
- 划分
选定一个记录作为轴值,以轴值为基准将整个序列划分为两个子序列,轴值的位置在划分的过程中确定,并且左侧子序列的所有记录均小于或等于轴值,右侧子序列的所有记录均大于或等于轴值; - 求解子问题
分别对划分后的每一个子序列递归处理; - 合并
由于对子序列的排序是就地进行的,所以合并不需要执行任何操作
实现:
int Partition(int r[],int low, int high){
int p=r[low];
while (low<high){
while(low<high&&r[high]>p)
high--;
r[low]=r[high];
while(low<high&&r[low]<p)
low++;
r[high]=r[low];
}
r[low]=p;
return low;
}
void quickSort(int r[],int low,int high){
if (low>=high)return;
int p=Partition(r,low,high);
quickSort(r,low,p);
quickSort(r,p+1,high);
}
最大字段和问题
问题:
给定由 n 个整数(可能有负整数)组成的序列(a1, a2, …, an),最大子段和问题要求字串和的最大值。例如,序列(-20, 11, -4, 13, -5, -2)的最大子段和为 20
分析:
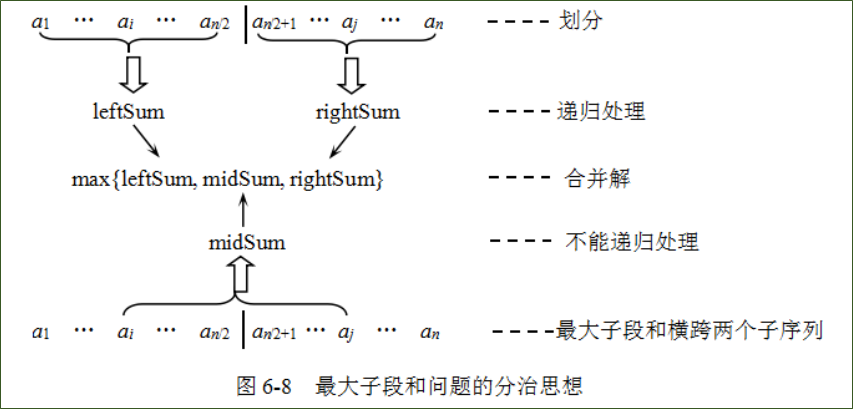
- 划分
划分为(a1, …, an/2 )和(an/2+1, …, an),则会出现以下三种情况:- (a1, a2, …, an)的最大子段和 = (a1, …, an/2 )的最大子段和;
- (a1, a2, …, an)的最大子段和 = (an/2+1, …, an)的最大子段和;
- (a1, a2, …, an)的最大子段和在中间
- 求解子问题
分别求解划分阶段的三种情况 - 合并
取三者之中的较大者为原问题的解。
实现
int maxSum(int t[],int left,int right){
int sum=0,leftSum=0,rightSum=0,centerSum=0,center=0;
if (left==right)
sum = t[left];
else{
center=(left+right)/2;
leftSum=maxSum(t,left,center);
rightSum=maxSum(t,center+1,right);
//求解第三种情况
//左侧最大
int lefts=0,s1=0;
for (int i = center; i >= left; i--){
lefts+=t[i];
if(lefts>s1) s1=lefts;
}
//右侧最大
int rights=0,s2=0;
for (int i = center+1; i <=right; i++){
rights+=t[i];
if(rights>s2) s2=rights;
}
centerSum=s1+s2;
}
if(centerSum<leftSum)
sum=leftSum;
else
sum=centerSum;
if(sum<rightSum)
sum=rightSum;
return sum;
}
棋盘覆盖问题
问题:
在一个\(2^k×2^k\) 个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用 4 种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2 个L型骨牌不得重叠覆盖
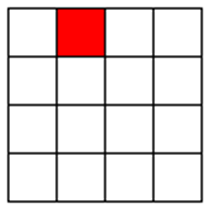
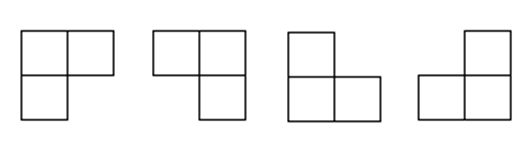
想法:
将整个棋盘平均划分4个区域,在中间放置一个骨牌,因此每个区域都包括一个特殊方格,将问题转化为4个子问题。
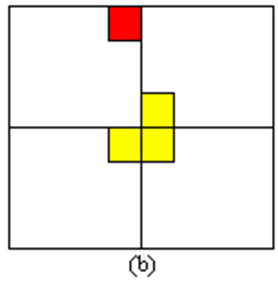
实现:
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
int s, t1;
if (size == 1) return;
t1 = ++t;
s = size/2;
if (dr < tr + s && dc < tc + s)
ChessBoard(tr, tc, dr, dc, s);
else{
board[tr + s - 1][tc + s - 1] = t1;
ChessBoard(tr, tc, tr+s-1, tc+s-1, s);
}
if (dr < tr + s && dc >= tc + s)
ChessBoard(tr, tc+s, dr, dc, s);
else {
board[tr + s - 1][tc + s] = t1;
ChessBoard(tr, tc+s, tr+s-1, tc+s, s);
}
if (dr >= tr + s && dc < tc + s)
ChessBoard(tr+s, tc, dr, dc, s);
else {
board[tr + s][tc + s - 1] = t1;
ChessBoard(tr+s, tc, tr+s, tc+s-1, s);
}
if (dr >= tr + s && dc >= tc + s)
ChessBoard(tr+s, tc+s, dr, dc, s);
else {
board[tr + s][tc + s] = t1;
ChessBoard(tr+s, tc+s, tr+s, tc+s, s);
}
}
最近对问题
问题:
要求在包含n个点的集合中找出距离最近的两个点。严格地讲,距离最近的点对可能多于一对,简单起见,只找出其中的一对即可
分析:
- 划分
利用\(x=m\)将点集划分为两个子集,其中m为中位数,每个子集包含n/2个点,最近的点有三种情况:- 最近的点在左子集中
- 最近的点在右子集中
- 最近的点横跨两个子集
- 求解子问题
- 同在一个子集中:递归解决
- 不在一个子集中:取\(d=min\{d_1,d_2\}\),可能出现最近距离的点必然在\([m-d,m+d]\)的范围内,因此只需在这个范围内搜索即可
- 合并
实现
//默认x坐标都是从小到大排列的
double closedPoint(int x[],int y[],int low,int high){
if(high-low==1){
return sqrt((x[low]-x[high])*(x[low]-x[high])+(y[low]-y[high])*(y[low]-y[high]));
}
int mid=(low+high)/2;
double d1=closedPoint(x,y,low,mid);
double d2=closedPoint(x,y,mid,high);
//第三种情况
double d=min(d1,d2);
int i,j;
for(i=mid;i>=low;i--){
if(x[mid]-x[i]>d){
break;
}
for(j=mid+1;j<=high;j++){
if(x[j]-x[mid]>d){
break;
}
double d3=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
if(d3<d){
d=d3;
}
}
}
return d;
}
练习
-
- 题目:分治法求最大元素
- 实现:
int max(int a[],int low,int high){ if(low==high){ return a[low]; } int mid=(low+high)/2; int max1=max(a,low,mid); int max2=max(a,mid+1,high); return max1>max2?max1:max2; } -
- 题目:分治法,数组循环左移k位
- 分析:前后分别翻转,再整体翻转
- 实现:
void reverse(int a[],int low,int high){ while(low<high){ int temp=a[low]; a[low]=a[high]; a[high]=temp; low++; high--; } } void leftMove(int a[],int n,int k){ reverse(a,0,k-1); reverse(a,k,n-1); reverse(a,0,n-1); } -
- 题目:递归n个元素全排列
- 实现:
void perm(int a[], int k, int m) { int i; if (k > m) { for (i = 0; i <= m; i++) cout<<a[i]; cout<<endl; } else { for (i = k; i <= m; i++) { swap(a[k], a[i]); perm(a, k + 1, m); swap(a[k], a[i]); } } } -
- 题目:有序序列\((r_1,r_2,r_3,...r_n)\),有\(i\)使得\(r_i=i\),用分治法求i;
- 分析:二分查找
- 实现:
int find(int a[],int low,int high){ if(low>high){ return -1; } int mid=(low+high)/2; if(a[mid]==mid){ return mid; }else if(a[mid]>mid){ return find(a,low,mid-1); }else{ return find(a,mid+1,high); } } -
- 题目:\(n\times n\)的二维数组,从左到右,从上到下升序排列,分治查找
- 分析:二分查找
- 实现:
int find(int *a[],int s, int n, int x){ int mid = (s+n)/2; if(s>n) return -1; if(a[mid][mid]==x) return mid; if(a[mid][mid]>x) return find(a,s,mid-1,x); else return find(a,mid+1,n,x); } -
- 题目:分治法逆序个数
- 分析:归并排序
- 实现:
int merge(int a[],int low,int mid,int high){ int i=low,j=mid+1,k=0; int temp[high-low+1]; int count=0; while(i<=mid&&j<=high){ if(a[i]<=a[j]){ temp[k++]=a[i++]; }else{ temp[k++]=a[j++]; count+=mid-i+1; } } while(i<=mid){ temp[k++]=a[i++]; } while(j<=high){ temp[k++]=a[j++]; } for(i=0;i<k;i++){ a[low+i]=temp[i]; } return count; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号