模拟法

概述

模拟法，对于很难通过数学推导找到规律的问题，采用模拟法直接模拟问题中事物的变化过程，是最简单的算法设计技术。

设计思想

对问题进行抽象，将现实世界的问题映射成计算机能够识别的符号表示。

例题

鸡兔同笼

题目：🐓有两只脚，🐇有四只脚，已知脚的数量，最多多少动物，最少多少动物。

void Feet(int n,int &maxNum,int &minNum){
    //如果n为奇数，则没有解
    if(n%2==1){
        maxNum=-1;
        minNum=-1;
        return;
    }
    //如果n为4的倍数，则最大值为n/2，最小值为n/4
    else if (n%4==0){
        maxNum=n/2;
        minNum=n/4;
        return;
    }
    //如果n为2的倍数，则最大值为n/2，最小值为n/4+1
    else{
        maxNum=n/2;
        minNum=n/4+1;
        return;
    }
}

约瑟夫环

题目：n个人围坐一圈，从1开始报数，报到m者出圈，输出最后一个出圈的人

void JosephusCircle(int n,int m){
    int *p=new int[n];
    for(int i=0;i<n;i++){
        p[i]=0;
    }
    int count,i=-1,num=0;
    while(num<n-1){
        count=0;
        while(count<m){
            i=(i+1)%n;
            if (p[i]==0)
                count++;
        }
        p[i]=1;
        num++;
    }
    for(int j=0;j<n;j++){
        if(p[j]==0){
            cout<<j+1<<endl;
            break;
        }
    }
}

埃拉托色尼筛法

题目：确定给定区间[1,n]内的素数，方法如下，依次标记2，3，4……n/2的倍数，未被标记的为素数。

void EratoSieve(int A[],int n){
    for(int i=2;i<=n/2;i++){
        //跳过已经被标记的数
        if(A[i]==1){
            for(int j=2;i*j<=n;j++){
                A[i*j]=0;
            }
        }
    }
}

计数排序

题目：对于每一个元素\(x\),记录小于\(x\)的记录的个数，然后把\(x\)放在对应的位置
分析：

1. 利用新数组num[],先统计记录待排序数组中各个元素的数量
2. 根据统计结果再计算每个元素小于等于自己的元素数量，存回num[]中；
3. 将原数组中数值x放在新数组中num[x]-1的位置，同时将num[x]的值-1；
4. 输出新数组

void countSort(int a[],int n){
    int num[n]={0};
    for (int i = 0; i < n; i++){
        num[a[i]]++;
    }
    for (int i = 1; i < n; i++){
        num[i]+=num[i-1];
    }
    int output[n];
    for (int i = n-1; i >= 0; i--){
        output[--num[a[i]]]=a[i];
    }
    for (int i = 0; i < n; i++){
        a[i]=output[i];
    }
}

颜色排序

问题：有红绿蓝三种颜色混合排列在数组中，将他们按红绿蓝的顺序将相同的颜色排列在一起
分析：

1. 快速排序变种
2. 设置三个指针i,j指向数组头，k指向数组尾
3. j从左往右遍历，若遍历到红色，则与i交换；交换后两者右移一位；
4. 若j遍历到蓝色，则与k交换，交换后k左移一位；

   注意这里j不左移，因为交换过来的可能是红色；需要继续判断；

5. j==k时停止判断

void colorSort(int a[],int n)
{
    int low=0,mid=0,high=n-1;
    while(mid<=high)
    {
        if(a[mid]==0)
        {
            swap(a[low],a[mid]);
            low++;
            mid++;
        }
        else if(a[mid]==1)
        {
            mid++;
        }
        else
        {
            swap(a[mid],a[high]);
            high--;
        }
    }
}

装箱问题

问题：分别有\(1×1，2×2，3×3，4×4，5×5，6×6\)大小的物品，放入\(6×6\)大小的箱子里，问需要箱子的个数
分析：

1. 依次分析情况

   产品	个数	剩余1×1	剩余2×2
   6×6	1	0	0
   5×5	1	0	11
   4×4	1	5	0
   3×3	1	5	7
   3×3	2	3	6
   3×3	3	1	5
   3×3	4	0	0
   2×2	9	0	0
   1×1	36	0	0

2. 由分析可知，\(4×4，5×5，6×6\)总要占一个箱子，\(3×3\)的箱子留下的空间可以放\(2×2,1×1\) 箱子，但是无法被放入\(4×4，5×5，6×6\)剩下的空间
3. 用\(4×4，5×5，6×6\)和\(3×3\)整除后的空间放入\(2×2,1×1\) 箱子
4. 向上取整

int Packing(int k1,int k2,int k3,int k4,int k5,int k6){
    int p2[4]={0,5,3,1};
    int n,x,y=0;
    n+=(k3+3)/4+k4+k5+k6;
    //x是剩余2x2空间的数量
    x=k4*5+p2[k3%4];
    if(k2>x){
        n+=(k1-x+8)/9;
    }
    //y是剩余1x1空间的数量
    y=36*n-36*k6-25*k5-16*k4-9*k3-4*k2;
    if(k1>y){
        n+=(k1-y+35)/36;
    }
    return n;
}

数字回转方阵

问题：输出如下矩形：
、

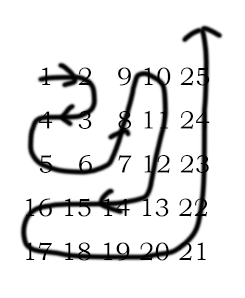void full(int n){
    //创建大小为n*n的矩阵
    int **a=new int*[n];
    for(int i=0;i<n;i++){
        a[i]=new int[n];
    }
    int num=1;
    a[0][0]=num++;
    for(int i=0,j=1;i<n&&j<n;){
        while (i<j){
            a[i++][j]=num++;
        }
        while (j>=0){
            a[i][j--]=num++;
        }
        i++;j=0;
        while (i>j){
            a[i][j++]=num++;
        }
        while(i>=0){
            a[i--][j]=num++;
        }
        j++;i=0;
    }
    //打印数组
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
}

逢7过

题目：输出1-100的整数，不包括7的倍数或带有7的数字；

void expSeven(){
    for(int i=0;i<100;i++){
        if (i%7==0||i/10==7||i%10==7);
        else cout<<i<<endl;
    }
}