MjAyNS4xMi4xNyBXYXRjaCBTb2x1dGlvbiBSZWNvcmQ=

QOJ4788 Gravity（\(\mathbf{Hard. 0}\)）

题目描述

给定一个 $N×M$ 的二进制矩阵。单元格 $(i,j)$ 如果空闲则包含字符 "."，如果被碎片占据则包含字符 "#"。每个 "#" 字符的最大 $4$ 连通分量形成一个不可分割的碎片。在下面描述的过程中，碎片不会以任何方式合并或分裂。属于同一碎片的所有单元格将以完全相同的方式移动。

碎片开始以相同的速度向地面（矩阵的最后一行）下落。碎片向下移动时不会旋转。每秒，所有碎片都尝试向下移动一行。如果这个运动导致碎片越过矩阵的下边界，则该碎片在原地停止。类似地，如果这个运动导致碎片与另一个碎片重叠（注意这只有在后一个碎片没有移动时才会发生），那么前一个碎片也会在原地停止。换句话说，当碎片碰到地面或碰到另一个碎片时，它们停止下落。

输出所有碎片停止下落后矩阵的最终状态。

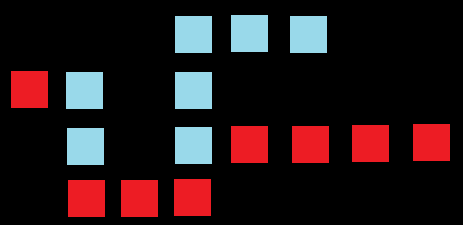
注意到对于每一列，连通块的相对顺序是不会发生变化的。我们只需要求出每个红色方块所能在的最低位置，就可以确定一个连通块。

我们按照连通块从下往上的顺序访问，求出每个块最低的一行的行坐标即可。

假设 \(p_i\) 为编号为 \(i\) 的连通块最终下落了多少，那么有 \(p_x \geq p_y + w\) 状物的不等式，差分约束系统即可。

点击查看代码

#include <bits/stdc++.h>
using namespace std; const int N=2007,dx[]={0,1,0,-1},dy[]={1,0,-1,0};
struct Node{int d,x,y;bool operator<(const Node &x)const{return d>x.d;}}u;
int n,m,i,j,k;char c[N][N],a[N][N];bool v[N][N];
int main() {
	cin>>n>>m;for(int i=1;i<=n;i++){cin>>c[i]+1;for(j=1;j<=m;j++)a[i][j]='.';}
	priority_queue<Node>q;for(j=1;j<=m;j++)q.push({0,n+1,j});
	while(!q.empty()){
		u=q.top();q.pop();if(u.x<1||u.x>n+1||u.y<1||u.y>m||v[u.x][u.y]||c[u.x][u.y]=='.')continue;
		v[u.x][u.y]=1,a[u.x+u.d][u.y]='#';if(u.x<=n)for(k=0;k<4;k++)q.push({u.d,u.x+dx[k],u.y+dy[k]});
		for(k=u.x-1;k>=1;k--)if(c[k][u.y]=='#'){q.push({u.d+u.x-k-1,k,u.y});break;}}
	for(i=1;i<=n;i++)puts(a[i]+1);
}

QOJ4786 Balance（\(\mathbf{?}\)）

咕咕嘎。

QOJ4795 Taxi（\(\mathbf{?}\)）

咕嘎咕。

QOJ4784 Battleship: New Rules（\(\mathbf{?}\)）

咕嘎嘎。

QOJ4802 Ternary Search（\(\mathbf{?}\)）

题目描述

最近，Grammy 在 Tony 的课上学到了三分查找。当数组是单峰（unimodal）时，她可以使用这种算法找到数组中的峰值。这里，我们称一个数组 $a_{1}, a_{2},\ldots, a_{n}$ 是单峰的，当且仅当它满足以下条件之一：

• 存在一个下标 \(k\) (\(1 ≤ k ≤ n\))，使得 \(a_{1} < a_{2} < \ldots < a_{k} > a_{k+1} > \ldots > a_{n}\)。

• 存在一个下标 \(k\) (\(1 ≤ k ≤ n\))，使得 \(a_{1} > a_{2} > \ldots > a_{k} < a_{k+1} < \ldots < a_{n}\)。

作为 Grammy 的导师，Tony 想检验 Grammy 是否完全理解了他课堂上所教的内容，因此他给 Grammy 留下了 n 个任务来尝试三分查找。任务如下：

最初，有一个空数组。每个任务会在数组的右端添加一个不同的数字，然后 Grammy 应该对其执行三分查找。然而，由于 Tony 的疏忽，在添加一些数字后，数组可能不再是单峰的。因为 Tony 已经睡觉去了，Grammy 只能自己解决这个问题。

对于每个任务，在 Grammy 尝试对其执行三分查找之前，需要执行一些操作使其变为单峰数组。在每次操作中，Grammy 可以交换 \(a_{i}\) 和 \(a_{i+1}\) 的值（对于某个 \(1 \leq i < n\)）。Grammy 是个懒惰的女孩，她觉得如果必须执行太多操作，她宁愿等 Tony 醒来解决问题。对于每个任务，她想知道要使数组变为单峰所需的最少操作次数是多少。你能帮助她吗？

QOJ2626 Kilk Not（\(\mathbf{?}\)）

嘎咕嘎。