UNR 6. D2T2 神隐
\(\mathbf{Part. -1}\)
这是一道交互题。
hehe 蚤决定花费几天时间,游览下山市的最著名的旅游景点 —— 吓山。
吓山,以高低纵横,崔巍秀丽,错综复杂的地形闻名。据说无论用什么地图导航,都不能保障你在山中不迷路。
之所以会出现这样的情况,是因为吓山中的路,在没有光的时候都会发生 “神隐”。在“神隐”状态下,人们无法察觉到这条路的存在,很容易就迷路了。
吓山的地图可以简化为一个 \(n\) 个节点,编号为 \(0 \sim n-1\) 的树。它有 \(n - 1\) 条边,其中第 \(i\) 条边为 \((u_i, v_i)\)(\(0 \leq i \lt n - 1\))。每条路上都装有路灯。
为了攻略吓山,hehe 蚤和它的小伙伴们试图绘制吓山的地图。
- hehe 蚤事先从吓山管理员那里拿到了吓山每条路的路灯的控制权。hehe 蚤会进行若干次询问,每次询问时 hehe 蚤都会打开一部分路的路灯,并关闭剩下的路灯。当一条路上的路灯打开时,这条路就真实存在;当路灯关闭时,这条路就会 “神隐”,等效于不存在。
- 对于每个询问,hehe 蚤的小伙伴们都会进行一番实地考察,告诉 hehe 蚤吓山在当前状态下的哪些节点是可以通过道路相互连通的。
- 最后 hehe 蚤会根据询问结果总结出一份地图,即恢复出这棵树的形态。
为了更高效地解决问题,hehe 蚤将其抽象为了一道交互题。有一棵未知的树,你需要对交互库进行若干次询问,来恢复这棵树的形态。每次询问时,你需要给出一个长度为 \(n - 1\) 的 \(01\) 向量 \(A\),然后交互库会将每条满足 \(A_i = 1\) 的边 \((u_i, v_i)\) 加入一张新的空图 \(G\) 中,并返回其中每一个连通块(再删除这个图)。最后,你需要输出这棵树的所有边(顺序、方向任意)。
\(\mathbf{Part. 1}\)
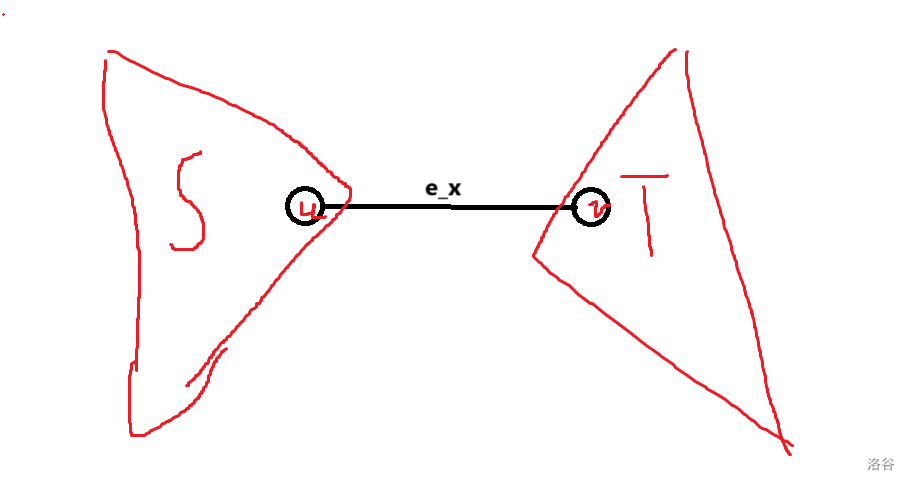
我们定义 \(e_x\) 表示第 \(x\) 条边。我们说 \(e_x\) 连接的两个连通块分别为 \(S_x, T_x\)(如下图)。
我们考虑观察每条边需要的询问信息。如果说对于一个询问,第 \(x\) 条边存在,则 \(u\) 和 \(v\) 在同一连通块内;第 \(x\) 条边不存在,则 \(u\) 和 \(v\) 不属于同一连通块内。考虑哪一种情况信息更多。
- 对于第 \(x\) 条边存在的所有询问,假设询问集为 \(Q\)。对于这些询问,我们只知道 \(x\) 在分别每个询问中不可能连接哪些点。我们可以尝试保证在这些询问中,除 \(e_x\) 外每条边都至少不存在一次1。显然,只有 \((u, v)\) 这一个点对对于所有询问,\(u, v\) 都一直在同一连通块中。
- 对于第 \(x\) 条边不存在的所有询问,假设询问集为 \(Q\)。对于这些询问,我们只知道 \(x\) 在分别每个询问中可能连接哪些点。我们可以尝试保证在这些询问中,除 \(e_x\) 外每条边都至少存在一次。对于 \(a\in S_x, b\in T_x\),都有 \((a,b)\) 点对,对于所有相关询问,\(u, v\) 不属于同一连通块(但是 \((a,b)\) 不一定是一条边,它可以是一条路径)。
综上,列出上述两种情况的结论:
- 只有 \((u, v)\) 这一个点对,对于所有 \(x\) 边存在的询问,\(u, v\) 一直在同一连通块中,此时第 \(x\) 条边连接 \(u, v\)。
- 对于 \(a\in S_x, b\in T_x\),对于所有 \(x\) 边消失的询问,\((a, b)\) 不在同一连通块。此时,我们无法区分 \((a, b)\) 和真正的 \(u, v\)。
显然,第一种会更强。于是考虑分析第一种情况。
PS:实际上,第二种情况也可以做出这道题。
由 1 处,我们需要对于所有边 \(x\),在 \(x\) 存在的询问中,边 \(y\) 至少消失一次。因此,我们要考虑构造每个边 \(x\) 存在的询问集合 \(Q_x\),使得对于任意 \(i\neq j\),都有 \(Q_{i} \not\subseteq Q_j\)。(因为如果 \(Q_j \subseteq Q_i\),则 \(e_i\) 要么在 \(Q_j\) 中全部出现,要么在 \(Q_i\) 中存在询问没有出现)
这是一个经典问题,\(\binom{\text{limit}}{\frac{\text{limit}}{2}}\) 为最大值。具体见 CF1365G Secure Password 的 \(\mathbf{Part. 2}\)。复杂度瓶颈在于计算每条边是否一直在同一连通块,\(\mathcal{O}(n^2 \times \text{limit})\)。
\(\mathbf{Part. 2}\)
我们发现,如果想要去直接优化复杂度瓶颈,那将会非常困难,因为每一个可能的点对 \((u, v)\) 我们都要判断它可不可能是真的边。光是点对数量就有 \(\mathcal{O}(n^2)\) 个。
那优化方法显而易见:我们能不能对于点对分组,每次判断一个组内的点对,来减少计算量?这要求对于一个组内的点对可以一起判断,而且不能说存在 \(100\) 条边合法之类的事情发生。最好的话,我们要让同一组内合法的点对尽量少,比如说只有一个?
考虑按照点来对点对进行分组。对于第 \(x\) 个点,我们要一起判断对于所有 \(i \neq x\),\((x, i)\) 这个点对是否是真的边。显然,对于第 \(x\) 个点,存在 \(deg_x\) 个点对合法,而这个 \(deg_x\) 可能很大,比如菊花图。当然,\(deg_x\) 一定存在点非常小,树的叶子就一定是 \(1\)。
显然,一上来不可能去考虑 \(deg_x\) 很大的情况。通过化繁为简的思想,我们先从简单的情况入手,考虑寻找哪些分组只有一个合法点对。
假设我们当前在考虑 \(x\)。那么,如果它只有一个合法点对,说明 \(x\) 为叶子节点,而连接这个叶子节点的边则是合法点对。显然,当这条边存在时,考虑观察 \(x\) 所在的连通块大小,显然,肯定一直 \(> 1\)。但是当这条边不存在时,\(x\) 所在连通块大小永远为 \(1\),而这是非叶子节点做不到的(这时候,性质对象从边变成了点,所以计算量减少一个量级)。
因此,考虑维护每个点在所有询问中的连通块大小的情况。显然,在判断完最简单的叶子后,我们类似于 topo 排序把叶子删除,同时更新相邻点的连通块大小信息。一直剥叶子,化繁为简,即可通过这道题目。复杂度为 \(\mathcal{O}(n\times \text{limit}) = \mathcal{O}(n \log n)\)。
\(\mathbf{Part. +\infin}\)
这一部分是更新部分。
其实上面的方法是有漏洞的,我们不知道每个点的父亲节点!这样我们完全不能输出这颗树,而且这个还不是很好求。但是由于前面剥叶子的做法我们只需要删掉这个点,对于每个询问更新信息,是不需要知道每个点的父亲节点的,所以原树的拓扑序我们还是能求出来的。
那我们现在有什么信息?我们知道每个点所在的连通块信息,且知道每个点的拓扑序。
假设当前我们在计算第 \(x\) 个节点的父亲节点。\(x\) 所在的所有连通块中,深度最低的点(也是所有点的 LCA)显然是 \(x\) 的祖先。 而由于 1,在 \((x, fa_x)\) 这条边存在时,\((fa_x, fa_{fa_x})\) 肯定消失过至少一次。所以,肯定有一个 \(x\) 所属的连通块,这个连通块的 LCA 是 \(fa_x\)。因此,考虑对于所有连通块,寻找除了 LCA 为 \(x\) 的其他 LCA 深度最大的那个点。
但是我们不知道深度。怎么办呢?由于 \(x\) 所在的所有连通块,LCA 都是 \(x\) 的祖先,又由于有祖先关系的两个点,他们的深度关系可以通过拓扑序来判断,所以我们把深度改成拓扑序即可,寻找除了 LCA 为 \(x\) 的其他 LCA 拓扑序最小值,其中 LCA 是连通块中拓扑序的最大值。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号